三阶两点边值问题非平凡解的存在唯一性

翟成波,赵莉

(山西大学 数学科学学院,山西 太原 030006)

三阶两点边值问题非平凡解的存在唯一性

翟成波,赵莉

(山西大学 数学科学学院,山西 太原 030006)

研究一类新型的三阶两点边值问题,利用新的不动点定理给出了这类边值问题非平凡解的存在唯一性,并举例说明结论的合理性。

非平凡解;三阶微分方程;存在唯一性;φ-(h,e)-凹算子

0 引言

最近非线性三阶微分方程引起人们的极大兴趣,已经获得一些好的结论,见文献[1-10]。这些文章中所用的办法有锥拉伸锥压缩不动点定理,不动点指数定理,打靶法,Schauder不动点定理等。文献中考察的多为三阶微分边值问题的正解,讨论了正解的存在性与多重性,但对其唯一性讨论很少,几乎没有。因此,本文将考察三阶微分方程非平凡解的存在唯一性,这种结论也包含了正解的存在唯一性。我们的办法是新的不动点定理。

本文讨论一类新型的三阶两点边值问题:

(1)

其中b>0是一个常数,f∶[0,1]×R→R连续。当b=0时,这类问题在文献中被讨论过,给出了正解的存在性,但唯一性没有。当b>0时,这类问题没有被讨论过,我们将给出其非平凡解的存在唯一性。因此,本文的结论以及方法都是新的,对人们研究非线性边值问题起到了很好的参考作用。

1 预备知识

设(E,‖·‖)是实Banach空间,P是E中的一个锥,则P导出了E中的半序:

x≤y⟺y-x∈P,记θ是E中的零元。若存在常数M>0,对于x,y∈E且θ≤x≤y就有‖x‖≤M‖y‖,则称P是正规的,M称为正规常数。

算子A∶E→E满足:x≤y⟹Ax≤Ay,则称A是单调递增的。

定义1[11]算子A∶Ph,e→E满足:对任意x∈Ph,e以及λ∈(0,1),存在φ(λ)>λ使得A(λx+(λ-1)e)≥φ(λ)Ax+(φ(λ)-1)e,则称A是一个φ-(h,e)-凹算子。

引理1[11]假设P是正规的,算子A∶Ph,e→E是单调递增的φ-(h,e)-凹算子,Ah∈Ph,e,那么A在Ph,e中有唯一不动点x*。此外,对任意w0∈Ph,e,作迭代序列wn=Awn-1,n=1,2,…,则必有‖wn-x*‖→0(n→∞)。

2 主要结果

引理2 假设f∶[0，1]×(-∞，+∞)→(-∞，+∞)是连续的,那么下列边值问题:

(2)

(3)

证明 利用积分与边界条件即可得到。

引理3 格林函数G(t,s)具有下列性质:

定理1 假设

(H2)对λ∈(0,1),存在φ(λ)>λ使得

(H3)f(t,0)≥0且f(t,0)在[0,1]上不恒为0.

则有:边值问题(1)在Ph,e中有唯一非平凡解u*,这里e(t),h(t)如上所述。此外,对于w0∈Ph,e,作迭代序列

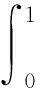
就有wn(t)→u*(t)(n→∞).

证明 首先,对于t∈[0,1],

即e∈P且有e≤h.此外,Ph,e={u∈C[0,1]|u+e∈Ph}.

由引理2可知,边值问题(1)等价于如下的积分问题

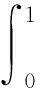
对于u∈Ph,e,λ∈(0,1),由(H2)可得

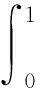
φ(λ)Au(t)+[φ(λ)-1]e(t).

因此可得A(λu+(λ-1)e)≥φ(λ)Au+[φ(λ)-1]e,u∈Ph,e,λ∈(0,1).所以,A是φ-(h,e)-凹算子。

最后,证明Ah∈Ph,e.由Ph,e的定义,只需证明Ah+e∈Ph.由引理3以及(H1)，(H3)可知,

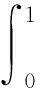
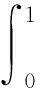
记

s.

由(H1)及引理3可得，

r1h(t)≤Ah(t)+e(t)≤r2h(t),t∈[0,1].

即r1h≤Ah+e≤r2h,因而就有Ah+e∈Ph.

显然，由(H3)可知，u*(t)在[0，1]不恒为0.即u*(t)是(1)的一个非平凡解。

此外,对任意的w0∈Ph,e,序列wn=Awn-1,n=1,2,…满足wn(t)→u*(t)(n→∞).

即

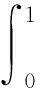
证毕。

由定理1的证明以及文[12]中的定理3,易得:

定理2 假设

(H4)f∶[0,1]×[0,+∞)→[0,+∞)连续,关于第二变量递增;

(H5)对于λ∈(0,1),存在φ(λ)>λ,满足f(t,λx)≥φ(λ)f(t,x),t∈[0,1],x∈[0,+∞);

(H6)f(t,0)在[0,1]上不恒为0.

那么,如下的三阶微分方程边值问题:

在Ph中具有唯一的正解u*,其中h(t)=t-t2.并且对任意w0∈Ph,迭代序列

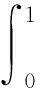
必收敛于u*(t),这里G(t,s)由(3)给出。

例1 考虑如下的三阶微分方程边值问题:

(4)

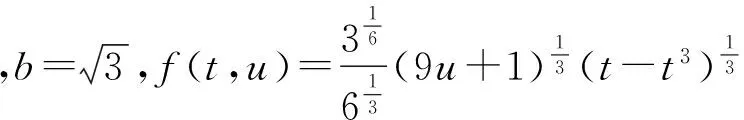
此外,

f(t,λx+(λ-1)y)={9e(t)[λx+(λ-1)y]+e(t)}

[1] Anderson D R,Davis J M.Multiple Solutions and Eigenvalues for Third-order Right Focal Boundary Value Problems[J].JMathAnalAppl,2002,267:135-157.DOI:10.1006/jmaa.2001.7756.

[2] Feng X F,Feng H Y,Bai D L.Eigenvalue for a Singular Third-order Three-point Boundary Value Problem[J].ApplMathComput,2013,219:9783-9790.DOI:10.1016/j.amc.2013.03.107.

[3] Feng Y Q,Liu S Y.Solvability of a Third-order Two-point Boundray Value Problem[J].ApplMathLett,2005,18:1034-1040.DOI:10.1016/j.aml.2004.04.016.

[4] Guo L J,Sun J P,Zhao Y H.Existence of Positive Solutions for Nonlinear Third-order Three-point Boundary Value Problems[J].NonlinearAnal,2008,68(10):3151-3158.DOI:10.1016/j.na.2007.03.008.

[5] Li Y H,Guo Y P,Li G G.Existence of Positive Solutions for Systems of Nonlinear Third-order Differential Equations[J].CommunNonlinearSciNumerSimulat,2009,14:3792-3797.DOI:10.1016/j.cnsns.2009.02.019.

[6] Lin X L,Zhao Z Q.Iterative Technique for a Third-order Differential Equation with Three-point Nonlinear Boundary Value Conditions[J].ElectJQualTheoryDiffEqu,2016,12:1-10.DOI:10.14232/ejqtde.2016.1.12.

[7] Padhi S.On the Asymptotic Behaviour of Solutions of Third Order Delay Differential Equations[J].GeorgianMathematicalJournal,2015,2:369-376.DOI 10.1007/s12215-014-0169-3.

[8] Wang F,Cui Y.On the Existence of Solutions for Singular Boundary Value Problem of Third-order Differential Equations[J].MathematicaSlovaca,2015,60(4):485-494.DOI:10.2478/s12175-010-0027-5.

[9] Xie W Y,Pang H H.The Shooting Method and Integral Boundary Value Problems of Third-order Differential Equation[J].AdvDifferEqu,2016:138.DOI:10.1186/s13662-016-0824-4.

[10] Zhao C,Zhou Q.On the Asymptotic Behavior of Solutions for a Third-order Nonlinear Differential Equation[J].VietnamJMath,2011,39(1): 71-77.

[11] Zhai C B,Wang L.φ-(h,e)-concave Operators and Applications[J].JMathAnalAppl,2017,454:571-584.DOI:10.1016/j.jmaa.2017.05.010.

[12] Zhai C B,Wang F.Properties of Positive Solutions for the Operator EquationAx=λxand Applications to Fractional Differential Equations with Integral Boundary Conditions[J].AdvDiffEqua,2015:1-10.DOI:10.1186/s13662-015-0704-3.

Existence and Uniqueness of Nontrivial Solutions for Third-order Two-point Boundary Value Problems

ZHAI Chengbo,ZHAO Li

(School of Mathematical Sciences,Shanxi University,Taiyuan 030006,China)

This paper considers a new form of third-order two-point boundary value problem. By using a new fixed point theorem, the existence and uniqueness of nontrivial solutions for the boundary value problem is obtained. In addition, an example is given to illustrate the main result.

nontrivial solutions;third-order differential equation;existence and uniqueness;φ-(h,e)-concave operator

10.13451/j.cnki.shanxi.univ(nat.sci.).2017.03.004

2017-05-10；

2017-05-24

国家自然科学基金(11201272)；山西省自然科学基金(2015011005)

翟成波(1977-),男,博士，教授,主要研究方向:非线性泛函分析与微分方程。E-mail:cbzhai@sxu.edu.cn

O175

A

0253-2395(2017)03-0416-05