在教学中践行“三个理解”
——以《基本不等式(第1课时)》的教学为例

陈义明

(北京市顺义牛栏山第一中学 101301)

人教社的章建跃老师指出，“三个理解”(即理解数学、理解学生、理解教学)是教师专业化发展的基石，是数学教学质量的根本保证，也是广大数学教师在教改大潮中“以不变应万变”的法宝.在“三个理解”的指导下，近期笔者设计并讲授了《基本不等式(第1课时)》一课，整个过程中感触颇多.

1 整体把握来龙去脉，努力做到理解数学

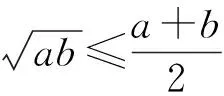
实际上，现实生活中的不等关系要远多于相等关系，它们都是客观事物的基本数量关系，是数学研究的重要内容．因此让学生建立不等观念就显得尤为重要，同时让学生学会处理不等关系与处理等量问题是同样重要的．

《课标》对不等式的内容安排做了整体布局，主要分三个部分：第一部分是《必修5》模块中，学习描述不等关系的数学方法、讨论不等式的基本性质，在此基础上建立了三个不等关系的模型：一元二次不等式、二元一次不等式(组)和基本不等式，并考虑它们的简单应用(如线性规划问题等)；第二部分在选修系列的“导数及其应用”中，以导数为工具研究函数的单调性、求解函数的极值(最值)，进而研究不等式的性质，另一方面也是将不等式作为研究函数的工具，利用不等式刻画函数的一些性质，在这个过程中体会导数方法在研究不等式问题中的一般性和有效性；第三部分是在选修4系列中安排《不等式选讲》专题，介绍一些重要的不等式和它们的证明，会用数学归纳法证明不等式．

直观想象是数学核心素养的一个重要方面，而几何图形是直观想象的一个重要载体，因此教材在叙述不等式相关内容时特别注重不等式及其证明的几何意义与背景，一方面学生可以借助图形“直达”不等式的数学本质，另一方面也加强了知识之间的联系，一定程度上发展了学生的逻辑推理以及分析解决问题的能力.

而对于基本不等式，它的结构简单：两个正实数通过加法、乘法、除法和开方四种基本运算，产生了它们的算数平均数和几何平均数的内在规律，体现了运算带给数的巨大力量．同时，基本不等式还可以从不同角度进行理解，并且不同角度都可以找到相应的知识背景，也就是说基本不等式能与很多知识进行融合．这样，在理解基本不等式的过程中就可以加强知识间的相互联系，并让学生体会其中所蕴含的数学思想．因此，“基本不等式”成为高中数学课程中与其他数学知识关联性极强的一个模块．

通过以上的分析，我们就可以对“基本”有一个基本认识：“基本”可以从运算的角度考虑(只运用加、乘、除、开方等基本运算)；还可以从证明的多样性(结合相应的背景，从不同角度进行解释)；还有就是它变形的多样性(由基本不等式出发推出其他不等式).

有了这些认识，我们就能意识到在第1课时中我们能做的东西其实不多：对于运算的体会是贯穿数学学习始终的，我们不可能期望学生通过一节课就能有一个质的飞跃；而对于证明方法的多样性以及变形的多样性，需要有一个知识的积累过程，也不可能在短时间内完全解决.这就要求我们要立足于整体设计“基本不等式”这一个“单元”的内容，而本节课是作为这一个“单元”的起始课.

2 关注思维“最近发展区”，真正做到理解学生

要做到理解学生，就要充分关注学情.上面我们指出，教材特别注重不等式及其证明的几何意义与背景，因此本节课的引入是从学生熟悉的弦图开始，由弦图抽象出重要不等式(a2+b2≥2ab(a,b∈R))，进而通过替换得到基本不等式.从学生的“最近发展区”出发(学生在初中已经接触过弦图：利用弦图证明勾股定理等)，便于学生接受，同时让学生体会“由形到数”的数学思想方法.

师：通过赵爽弦图，我们层层递进，得到了不等式a2+b2≥2ab(a,b∈R)，你能否用文字语言叙述一下这个不等式所反映出的规律.

学生听到这个问题后有点发懵，不知如何回答，此时教师不插话，任由学生思考……

生1：任意两个实数的平方和大于等于它们乘积的2倍.

生2：任意两个实数的平方和不小于它们乘积的2倍.

师：说得非常好，这就是对式子的直接“翻译”.

生3：左边不就是两个正数(实际上是非负数)的和吗，但是右边我说不好.

师：你感觉什么地方说不好呢？

生3：我觉得右边式子需要考虑a,b的正负才能说清楚，但那样就太烦了.

师：你表达得已经很好了.生3同学关注到了两个非负数的和与一个乘积的大小关系，但是那个乘积好像不太好直接叙述，我们暂且把这个问题搁置起来，看看后面有没有好的方法解决.

师：跟刚才一样，你能否用文字语言叙述一下这个不等式所反应出的规律.

生3：两个正数的和不小于它们平方根乘积的2倍.

生4：应该是它们算术平方根的乘积吧！

师：看来生3同学还是说不好啊！(同学们都哄笑)但是通过他的叙述我们发现这个不等式所反映出的规律跟重要不等式是一致的，从某种程度上说这个不等式更为简洁.所以说生3同学的贡献还是很大的.(同学们都鼓掌)

基本不等式的证明是让学生将不同知识联系起来的很好的载体，学生可以从多种角度进行思考：作差法、构造函数、构造向量、构造几何图形等. 基于重要不等式的得出是通过“由形到数”的方式，而引导学生“由数到形”探究基本不等式的几何解释，可以发展学生的辩证思维，体会数形结合思想，提高学生的几何直观能力.

师：前面我们由赵爽弦图出发得到了重要不等式a2+b2≥2ab，也就是说重要不等式有明确的几何背景，而基本不等式所反映的规律又与它是一致的，那你能否找到基本不等式的几何背景呢，也就是对基本不等式做出几何解释.

学生的探究热情非常高……

图1

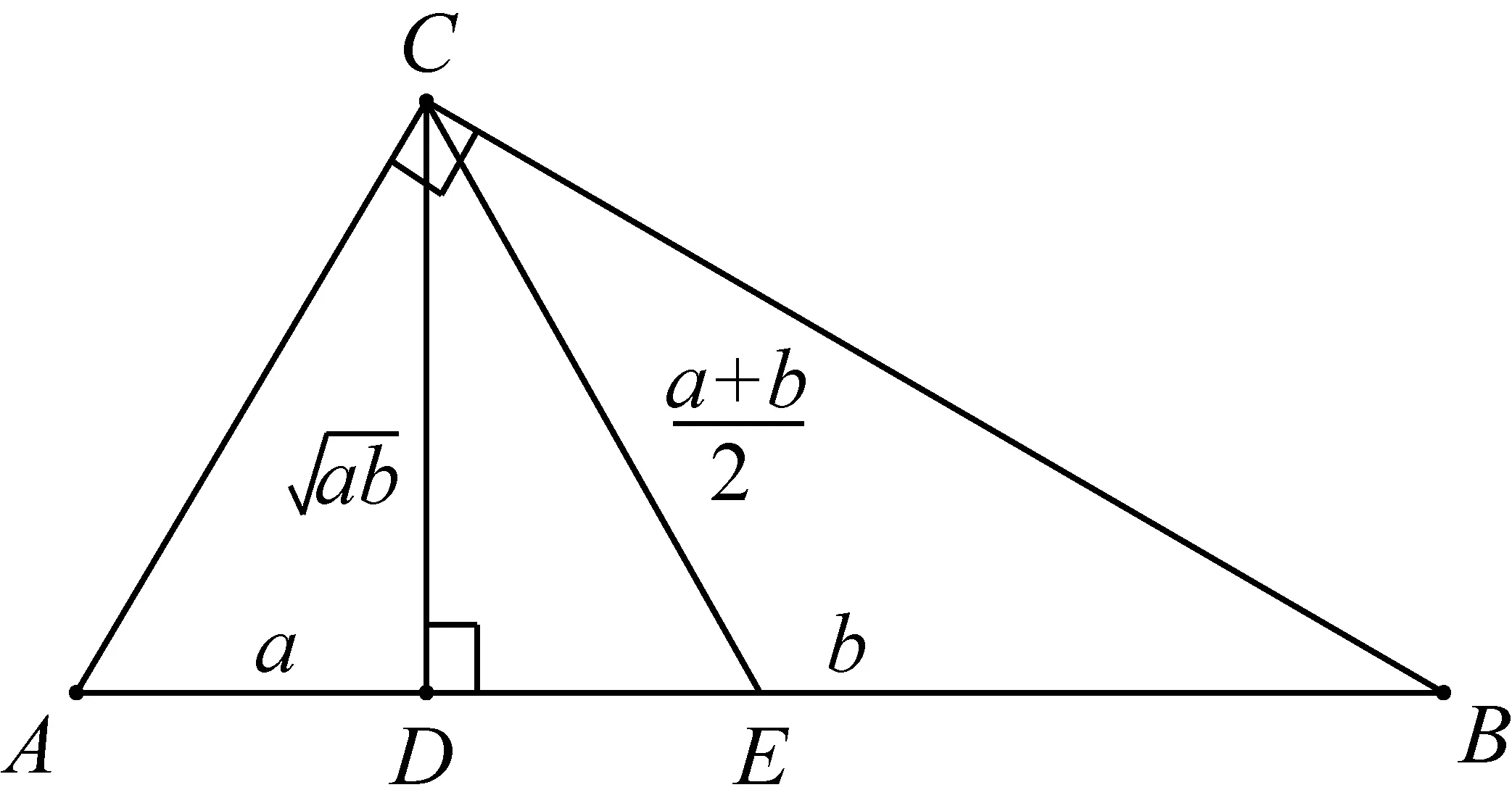
图2

师：什么时候等号成立呢？

生5：当且仅当D,E两点重合时，也就是a=b时.

师：说得非常好，生5同学利用直角三角形的性质给出了基本不等式的几何解释，他是先构造出了直角三角形斜边上的高，然后再令AD=a,BD=b.我如果给定两个正数a,b，你如何构造这样一个直角三角形呢？

经过短暂思考，下面学生就有说作圆的.

生6：采用作圆的方式.构造长度为a+b的线段AB；在其上取一点D，使得AD=a,DB=b；以线段AB为直径作⊙O；过点D作线段AB的垂线，交⊙O于点C，则Rt△ABC即是满足条件的直角三角形(如图3).

图3

师：非常好，这样我们就能构造出“双垂直”结构.那你能否利用圆中的元素对基本不等式进行解释呢？

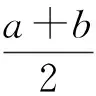
生7：刚才生6在“过点D作线段AB的垂线”时，垂线与圆是交于两点的，这两点都是满足条件的(设为C,E)，那么CE就是圆的弦，所以CD的长应该是这个弦长的一半.但是我不知道这样说对不对：圆中弦长的一半不大于半径.

生8：肯定是对的.

师：为什么？

生8：由“垂径定理”得到.

师：说的对，生7和生8两名同学合作就给出了基本不等式的又一种几何解释：圆中弦长的一半(即半弦长)不大于圆的半径.那什么时候相等呢？

学生共同回答：弦是直径的时候.

师：在图3中看，就是D,O重合，a=b的时候.

其实，理解学生就是用学生的眼光看数学，由浅入深，及时发现学生的思维障碍，由感性到理性地设计问题，逐步让学生走近问题的本质，让知识的产生和发展自然而流畅.

3 用数学整体观和系统思维理解教学

前面我们已经指出，就本节课的知识而言，学生不太可能理解“基本”到底体现在哪，需要后续不断地深化理解.因此教学设计兼顾单元教学.

本节课的内容是基本不等式的推导、证明及其几何解释，正确把握基本不等式的结构和等号成立的条件；第2课时的内容是能用基本不等式求简单的最值问题，并深入理解基本不等式成立的条件和结构特征；第3课时的内容是从实际问题中抽象出具体的基本不等式问题，并应用基本不等式处理最值问题，也就是将基本不等式作为处理优化问题的一种模型；第4课时考虑介绍一下基本不等式的变形及其应用，深化对基本不等式应用的理解；最后，在小结复习课中提出“为什么称它是基本不等式？”这样的问题，来检验学生对其本质的理解.同时，在本部分学习中设计一节活动课“基本不等式证明方法大全”，以小组为单位探究基本不等式的证明方法，激发学生学习数学的热情.

本节课作为“单元”教学的起始课，为达到单元的整体目标做了一些铺垫，比如在基本不等式的证明中设计它与不同知识之间的联系，并在证明中对基本不等式做了一些变形，这就是为了体现它“基本”的一面——证明的多样性与变形的多样性；同时，本节课通篇设计让学生体会“数形结合”思想：“由形到数”探求基本不等式的生成过程；“由数到形”探求基本不等式的几何解释，发展学生的辩证思维.在后面的学习中也这样设计，在解决问题中注重“数形结合”思想的应用，构建在数学方法上具有前后一致性的教学进程.

总之，对于一节课而言，理解数学是做好教学设计的前提，在教学设计中要有数学整体观，不要被“一节课”的内容所限制，更不要在一些细枝末节上纠缠，而是要引导学生通过探索、思考、辨析、反思等环节，直达问题的本质；理解学生可以提高教学效率、促进学生发展，在教学中我们必须充分关注学情，准确找到学生的“最近发展区”，让知识的发生和发展都自然而流畅；理解教学可以让课堂持续充满活力，充满活力的课堂才可能指引学生走向知识的数学本质，同时我们的教学要引导学生“知其然”以及“知其所以然”，更要让学生知道“何由知其所以然”.