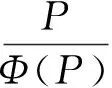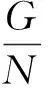有限群子群的正规化子与群的p-幂零性

张新建

(淮阴师范学院 数学科学学院, 江苏 淮安 223300)

0 引言

本文中所有的群皆为有限群,G代表有限群,其他符号和术语是标准的[1].

设G是群,H是G的子群,H称为在G中s-置换,如果H与G的每个Sylow 子群置换;H称为在G中c-正规,如果G有正规子群T满足G=HT且H∩T≤HG,其中HG为H在G中的柱心;H称为在G中弱s-置换,如果G有次正规子群T满足G=HT且H∩T≤HsG,其中HsG为包含在H中的G的极大s-置换子群;H称为在G中s-半置换,如果H与G的每个Sylowp-子群置换,其中(|H|,p)=1.Yang[2]等介绍了子群的弱s-半置换性质,其覆盖了上面的所有概念,并得到了定理1.

定义1[2]子群H称为在G中弱s-半置换,如果G有次正规子群T和包含在H中的G的s-半置换子群HssG满足G=HT且H∩T≤HssG.

定理1[2]设G为群,P为G的一个Sylowp-子群,其中p是G的阶的极小素因子.假设P有子群D满足1<|D|<|P|且P的每个阶为|D|的子群或者4阶循环群(当P非循环且|D|=2时)在G中弱s-半置换,则G是p-幂零群.

令p是一个素数,P为G的一个Sylowp-子群,NG(P)的性质对群的结构有重要影响,比如,著名的Burnside定理断言如果NG(P)=CG(P),则G是p-幂零群;Frobenius定理断言群G是p-幂零群如果对于G的所有p-子群H都有NG(H)是p-幂零群.将Frobenius 定理与弱s-半置换性质结合,得到了群Gp-幂零的两个准则:定理2和定理3,这两个定理可以看成是定理1的补充.

1 基本引理

接下来，给出证明主要结果所需的引理.

引理1[3]设G为群,则

1) 如果H≤K≤G,且H在G中s-置换,那么H在K中s-置换;

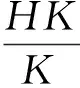
3) 如果P是群G的s-置换p-子群,那么NG(P)≤Op(G).

引理2[2]设G为群,H为G的s-半置换子群,则

1) 如果H≤K≤G,那么H在K中s-半置换;

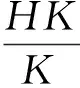
3) 如果H≤Op(H),那么H在G中s-置换.

引理3[2]设G为群,H为G的弱s-半置换子群,K是G的正规子群,则

1) 如果H≤T≤G,那么H在T中弱s-半置换;

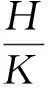
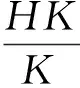
引理4[4]设P是群G的一个幂零正规子群且P∩Φ(G)=1,那么P是群G的某些极小正规子群的直积.

引理5[2]设N是群G的初等交换正规子群. 如果N有子群D满足1<|D|<|N|且N的所有阶为|D|的子群在G中弱s-半置换,则N的某个极大子群在G中正规.

引理6[5]设G为群,P为G的一个Sylowp-子群,其中p是素数. 如果P交换且NG(P)p-幂零,那么G是p-幂零群.

引理7[5]设G=PQ,P为G的一个Sylowp-子群,Q为G的一个Sylowq-子群, 其中p是奇素数,q≠p是素数. 假设NG(P)是p-幂零的. 如果Op(G)是P的极大子群且Op(G)的每个p阶循环子群在G中s-置换,那么G是p-幂零的.

2 主要结论

定理2 设p是整除群G的阶的奇素数,P为G的一个Sylowp-子群, 假设P有子群D满足1<|D|<|P|且P的每个阶为|D|的子群在G中弱s-半置换. 如果NG(P)是p-幂零的,那么G是p-幂零群.

证明假设结论错误,G是一个极小阶反例. 现在分以下步骤进行证明.

第1步:Op′(G)=1.

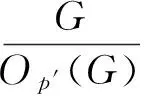
第2步: 如果M是G的包含P的真子群,则M是p-幂零群.

显然,NM(P)≤NG(P),因此NM(P)是p-幂零的,由引理3 的1)可知M满足定理的假设,于是由G的极小选择可知M是p-幂零群.

第3步:G=PQ,其中Q为G的一个Sylowq-子群,q≠p是素数,且CG(Op(G))≤Op(G).

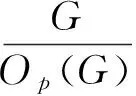
另一方面,因为Gp-可解,由定理[7],对于任意的q∈π(G)且q≠p,G有Sylowq-子群Q,满足PQ=QP是G的子群. 如果PQ

第4步: 如果|P:D|>p,那么对于G的每个正规极大子群M有|G:M|=p且M的Sylow子群P∩M=Op(G)是P的极大子群,1<|D|<|Op(G)|且Op(G)的每个阶为|D|的子群在G中s-置换.

设M为G的任一正规极大子群. 由第3步有,或者|G:M|=p或者|G:M|=q. 如果|G:M|=q,则由第2步知,M是p-幂零群,从而G是p-幂零群,矛盾. 所以|G:M|=p. 令P1=P∩M. 显然NG(P)≤NG(P1)≤G. 如果NG(P1)p,则M满足定理的假设,于是M是p-幂零群,从而G是p-幂零群,矛盾. 因此,可以假设NG(P1)=G. 于是,P1在G中正规. 因为NG(P)是p-幂零的,而G是非p-幂零的,Op(G)

因为|P:D|>p,有1<|D|<|Op(G)|. 令H为Op(G)的阶是|D|的子群. 由假设,G有次正规子群K和包含在H中的群G的s-半置换子群HssG满足G=HK且H∩K≤HssG. 如果HssG≠H,则K

第5步: |D|>p.

如果|D|=p且|P:D|>p,则由第3步,第4步和引理7可知G是p-幂零群,矛盾. 如果|D|=p且|P:D|=p,则|P|=p2,则由引理6同样可得G是p-幂零群. 因此|D|>p.

第6步： 设N为G的极小正规子群,则N≤Op(G)且|N|≤|D|.

由第1步和第3步知,N≤Op(G)是显然的. 假设|N|>|D|. 因为N是初等交换群,由引理5,N有极大子群在G中正规,矛盾于N的极小性. 因此|N|≤|D|.

第8步: 最后的矛盾.

如果|P:D|>p,则由第4步,有|P:N|=p,于是|N|>|D|,和第6步矛盾. 因此 |P:D|=p,即P的每个极大子群在G中弱s-半置换. 由第7步,G有极大子群M满足G=NM且N∩M=1. 因为Mp

推论1[8]设p是整除群G的阶的奇素数,P为G的一个Sylowp-子群, 如果NG(P)是p-幂零群且P的每个极大子群在G中c-正规,那么G是p-幂零群.

推论2[9]设p是整除群G的阶的奇素数,P为G的一个Sylowp-子群, 如果NG(P)是p-幂零群且P的每个极大子群在G中c-正规,那么G是p-幂零群.

定理3 设p是群G的阶的素因子,P为G的一个Sylowp-子群, 假设P有子群D满足1<|D|<|P|,P的每个阶为|D|的 子群H在G中弱s-半置换且NG(H)是p-幂零的,那么G是p-幂零群.

证明假设结论错误,G为极小阶反例.

假设H是P的阶为2的子群, 由假设,G有次正规子群K和包含在H中的群G的s-半置换子群HssG满足G=HK且H∩K≤HssG. 于是G=PK且P∩K在G中正规. 由P的极小性,或者P∩K=1或者P∩K=P. 如果前者是正确的,那么P=P∩HK=H(P∩K)=H,矛盾. 于是P∩K=P,即P≤K,于是H=H∩K=HssG. 由引理5的3)和引理1有,G=Op(G)≤NG(H)是p-幂零群,又一矛盾. 因此p是奇素数.

如果NG(P)

[1] Huppert B. Endliche Gruppen I[M].New York-Berlin: Springer,1967.

[2] Yang M L, Qiao S H, Su N , et al. On weaklys-semipermtable subgroups of finite groups[J].Journal of Algebra,2012,371:250-261.

[3] Kegel O H. Sylow-Gruppen and Subnoramlteiler endlicher Gruppen[J].Math Z,1962(78):205-221.

[4] Skiba A N. A note onc-normal subgroups of finite groups[J].Algebra Discrete Math,2005(3):85-95.

[5] Zhang X J, Li X H, Miao L. Sylow normalizers andp-nilpotence of finite groups[J].Comm Algebra,2015(43):1354-1363.

[6] Robinson D. A Course in the Theory of Groups[M].New York-Berlin: Springer-Verlag,1993.

[7] Gorensein D. Finite Groups[M].New York: Chelsea,1968.

[8] Guo X Y, Shum K P. Onc-normal maximal and minimal subgroups of Sylowp-subgroups of finite groups[J].Arch Math,2003,80:561-569.

[9] Wang L F, Wang Y M. Ons-semipermutable maximal and minimal subgroups of Sylowp-subgroups of finite groups[J].Comm Algebra,2006,34:143-149.