结构动力响应扩展离散解析模式分解的截止频率优化选取方法
后军军, 王佐才,2, 任伟新,2
(1.合肥工业大学土木与水利工程学院, 安徽 合肥 230009; 2.合肥工业大学桥梁结构安全监测新理论与新技术研究中心, 安徽 合肥 230009)
引 言
利用结构振动信号进行系统识别和损伤探测是当前的热点研究问题之一,特别是结构振动信号的瞬时特征,是进行结构参数识别和损伤识别的重要指标,对于评估结构状况具有十分重要的作用[1-2]。
为获得结构振动响应信号的瞬时特征,诸多时频分析方法,如短时傅里叶变换、小波变换、希尔伯特-黄变换等[3-5],被广泛应用于振动信号的响应分析之中。其中,基于希尔伯特变换的信号分析方法,可以通过定义单一信号分量的解析信号,并由此定义出单一信号分量的瞬时幅值和瞬时频率,该方法被广泛应用于实测振动信号的分析。然而基于希尔伯特变换的信号分析方法,首先需要获取结构单一的信号分量,因此,在利用希尔伯特变换进行振动响应分析前,需要对结构振动响应信号进行分解。其中希尔伯特-黄变换对信号进行经验模式分解,提取出本征模态函数,再对本征模态函数进行希尔伯特变换,得到其瞬时频率和幅值[6]。为了避免在经验模式分解的处理过程中出现模态混叠,提出了集合经验模式分解,集合经验模式分解可以从掺杂噪声的信号中恢复出原信号[7]。另外,Feldman[8]提出了希尔伯特振动分解。利用这一分解方法,可以将解析信号中的最大能量组分的瞬时频率通过低通滤波器提取出来;同时,运用相干探测技术也可以提取出该最大能量组分的瞬时幅值,并进一步在非线性特征参数的提取中获得应用[9]。
最近,Chen和Wang[10]提出了基于希尔伯特变换的解析模式分解方法,可以解析地提取出信号中的低频部分。解析模式分解算法可视作一个低通滤波器,并可滤除振动信号中的高频噪声干扰,也可用于具有密集模态的振动信号的分解[11-12]。通过对结构振动信号的解析模式分解和希尔伯特变换分析,此方法被进一步应用于时变非线性系统的参数识别之中[13-15]。但是,解析模式分解理论建立在信号为连续的前提条件下。当振动信号为离散信号时,运用上述传统的解析模式分解方法提取低频部分时会存在一些误差。同时,当信号中存在噪声或者非平稳部分时,会导致傅里叶谱出现扭曲,从而,难以找到信号分解的截止频率。为了避免振动信号傅里叶谱出现扭曲,提出了从功率谱出发研究对随机信号的频域分析方法。而功率谱估计是用有限长的数据来估计信号的功率谱,其中自回归功率谱模型法是功率谱估计的核心方法之一,其在实际工程中有着重要的应用价值,如在地震勘探信号处理、水声信号处理等多个领域中发挥了重要的作用[16]。为了更好地选择信号分解的截止频率,Lauria和Pisani[17]提出了利用LP非线性周期谱来获取信号解析模式分解中的截止频率。
针对结构中振动信号的离散性,论文首先提出了扩展离散解析模式分解,通过分析离散信号的特点,给出了离散信号的频响特征,进而给出了关于离散信号分解的两步分解法。为了更好地对截止频率进行自动化优化选取,提出用自回归功率谱代替传统的傅里叶谱选取截止频率的方法。以吉安赣江公路大桥为工程实例,验证了方法的有效性。
1 扩展离散解析模式分解
1.1 连续信号的解析模式分解
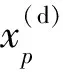
(1)
如果x(t)的每一主成分的频率满足:|ω1|<ωc1,|ωc1|<|ω2|<ωc2…ωc(n-1)<|ωn|<ωcn,其中ωcp为选取的截止频率。则每个信号分量可以表示为[10]:
(2)
sp(t)=sin(ωcpt)H[x(t)cos(ωcpt)]-
cos(ωcpt)H[x(t)sin(ωcpt)]
(3)
式(2)及(3)中s0(t)=0,H[·]表示对括号中的函数进行希尔伯特变换。理论的核心是利用截止频率ωc将原始信号中的低频部分s(t)提取出来,且s(t)能够由下式[10]获得。
(4)
因此式(4)就像一个低通滤波器,通过了信号的低频部分,滤掉了其高频部分。
1.2 离散解析模式分解
由于式(1)中的解析模式分解定理是源于对连续信号的推导,因此在适用于振动响应离散信号时,要求具有足够大的采样频率。因而,为了实现对离散信号的有效分析,进一步拓展了解析模式分解理论,提出离散解析模式分解理论。对于离散解析模式分解理论,可以表示为:对于一个具有N个样本点的离散信号:x(0),x(1),x(2),…,x(i),… (i=0,1,2,…,N-1),它的离散傅里叶变换可以表示为
(5)
式中k表示离散的频率分量。
由于该信号的离散傅里叶变换是以N为周期的,所以在一个基本周期内(0 ≤k≤N-1),定义的离散点k如图1所示。

图1 定义在离散傅里叶变换上的点k
Fig.1 The defined discrete point k for the discrete Fourier transform
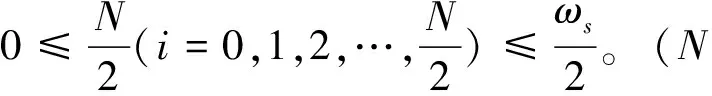
(6)

(7)

(8)

(9)
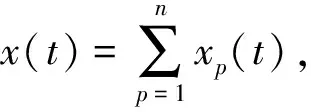
xp(t)=AP(t)cos(θp(t))
(10)
式中Ap(t)表示信号xp(t)的幅值,θp(t)为第p个分量的相位角。而对于离散信号,式(10)可以表示为
(11)
式中ωp(q)表示信号分量xp在时间点qΔt处的频率,θp0为信号分量xp的初始相位角。故式(4)的离散形式可以表示为
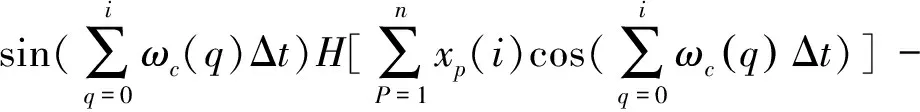
(12)
0<ω1(q)<ω2(q)<…<ωK1(q)<ωc(q)<
(13)
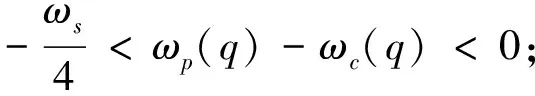
(14)


第二步:将第一步滤出的s′(t)作为输入信号,选择与第一步相同的截止频率,通过式(14)滤出信号s″(t)。
分别将滤出的s′(t)和s″(t)带入等式(14)中得到:
(15)
(16)
通过叠加等式(15)和(16),可以发现提取的低频信号的频率在任意时刻均小于截止频率
(17)
2 截止频率选取方法
扩展离散解析模式分解理论进行信号分解时,必须选取截止频率。所以,信号进行扩展离散解析模式分解的核心内容之一就是准确选取合适的截止频率。传统的截止频率的选取方法是将原始时间序列函数经过傅里叶变换获得频谱图,然后在频谱图中找到两极值之间的某个位置,而该位置所对应的频率值即可作为选定的截止频率。传统的截止频率的选取方法依赖于频谱图,一旦频谱图出现扭曲或者过于复杂时,就很难找到准确的截止频率。因此,用传统的截止频率选取方法选取截止频率时,往往会导致分解信号出现一定程度的误差。为了更好地准确地选择信号分解的截止频率,本文提出了一种基于自回归功率谱的截止频率选取方法。
2.1 自回归功率谱
随机信号的总能量是无限的,但其平均功率却是有限的,因此要对随机信号的频域进行分析,应从功率谱出发进行研究才有意义。功率谱估计是用有限长的数据来估计信号的功率谱,即利用给定的N个样本数据估计一个平稳随机信号的功率谱密度。而自回归功率谱模型法是功率谱估计的核心方法之一,其在实际工程中有着重要的应用价值,如在地震勘探信号处理、水声信号处理等多个领域中发挥了重要的作用。
信号的功率谱可以通过下式来进行计算
(18)
式中rx(m)为x(n)的自相关函数,N为x(n)的长度。
由于数据存在截断,所以功率谱的分辨率较低。同时,由功率谱密度的定义可知,信号的均值以及各段极值并不能准确求得,信号的方差也存在较大偏差。现阶段为了获得精确度较高的功率谱,一般采用参数模型功率谱估计,参数模型计算可根据下式获得
(19)
在式(19)中,假定x(n)为被白噪声u(n)激励的线性系统输出,p和q表示参数模型的阶数。当bk=0时,此时x(n)可由下式获得
(20)
式(20)所表达的参数模型即为自回归模型。
(21)
式(21)为自回归模型的标准方程式。通过式(21)可以计算出模型的参数ak和σ2。
综上所述,自回归功率谱pAR(ejω)可以由下式计算得到
(22)
式中σ2为u(n)的方差,p为自回归模型阶数。
对于功率谱的分辨率而言,谱的清晰度与信号的长度呈反比例关系为
(23)
式中 Δf为分辨率,T为信号的时长。
自回归功率谱是在最小均方差意义上给定的数据拟合,所以自回归功率谱有着更高的分辨率。但在保证自回归功率谱较高分辨率的同时,谱曲线中不出现实际不存在的虚假频段,需要选择合适的自回归模型阶数p。实际上,确定模型阶数的方法有多种,本文采用最终预测误差判据法[18-19]确定模型阶数。即当下式中FRE取得最小值时,k的取值即为最优的模型阶数p的值
(24)
式中N为离散信号长度,ρk为最小化预报错误的能量。
2.2 自回归功率谱选择截止频率
自回归功率谱的密度曲线是相对光滑的,分辨率也较高,这一特点为其代替傅里叶谱选择截止频率提供了优势条件。自回归功率谱选择截止频率的方法为:首先获得原始时间序列函数的自回归功率谱,考虑到自回归功率谱的密度曲线光滑、分辨率高、去噪强的特点,其密度曲线中每一个显著的谱峰就可以看成信号的一个单一模态,故可以取两相近谱峰极值的平均值所对应的频率作为选定的截止频率。实际计算自回归功率谱模型时,用于计算的算法有多种。考虑到算法的简洁性,本文选择伯格算法[20-21]计算自回归功率谱模型。
3 数值模拟
3.1 数值模拟1
以一个数值算例来验证上述扩展离散解析模式分解方法的有效性。离散时间序列x(t)由2个信号组成。
x(t)=x1(t)+x2(t),
x1(t)=e-3(t-0.4)sin[20π(t-0.4)]u(t-0.4),
x2(t)=e-2(t-0.2)sin[460π(t-0.2)]u(t-0.2)
其中u(t)为阶跃函数。采样频率为500 Hz,截止频率选为50 Hz。则原始时间序列函数如图2所示。
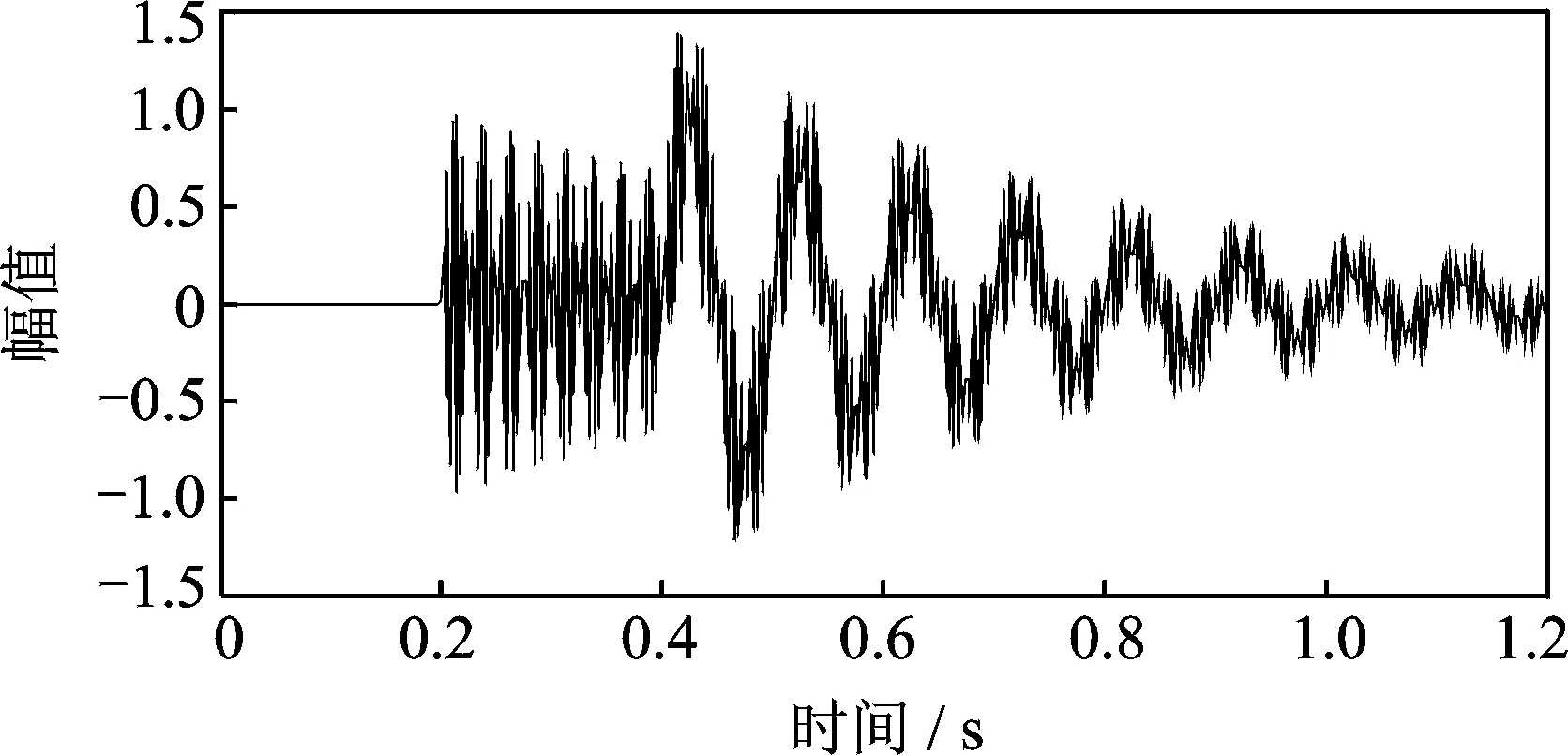
图2 原始信号x(t)Fig.2 The original signal x(t)

图3 一步低通滤波器滤波Fig.3 The one step low-pass filter

图4 两步低通滤波器滤波Fig.4 The two step low-pass filter
由图3和4的对比可以发现,在一步低通滤波器中分离出的低频部分与x1(t)有较大差异;而利用两步低通滤波器可以很好地从离散信号x(t)中提取低频部分x1(t)。所以,上述所述扩展离散解析模式分解对离散信号的低频部分的提取是有效的。
3.2 数值模拟2
为了验证上述截止频率选取方法的有效性,分析了一个带有4层附属层的36层框架结构。结构的每一层的质量和层间的刚度分别为1.29×106kg和1.0×109N/m。附属层的质量是主体层质量的2%,而附属层的层间刚度是主体层间刚度的0.03%。结构的阻尼假设为经典阻尼,其中前4阶模态的阻尼比均为1%,而其他高阶模态的阻尼比均为零。结构整体承受均值为零,方差为0.001g的高斯白噪声激励。结构顶层加速度响应如图5所示,其中采样频率为20 Hz。图6为顶层加速度响应的傅里叶变换,为了较为清楚地显示傅里叶谱图,图6的纵坐标为取以10为底的对数坐标。

图5 顶层加速度响应
Fig.5 The measured acceleration at the top level
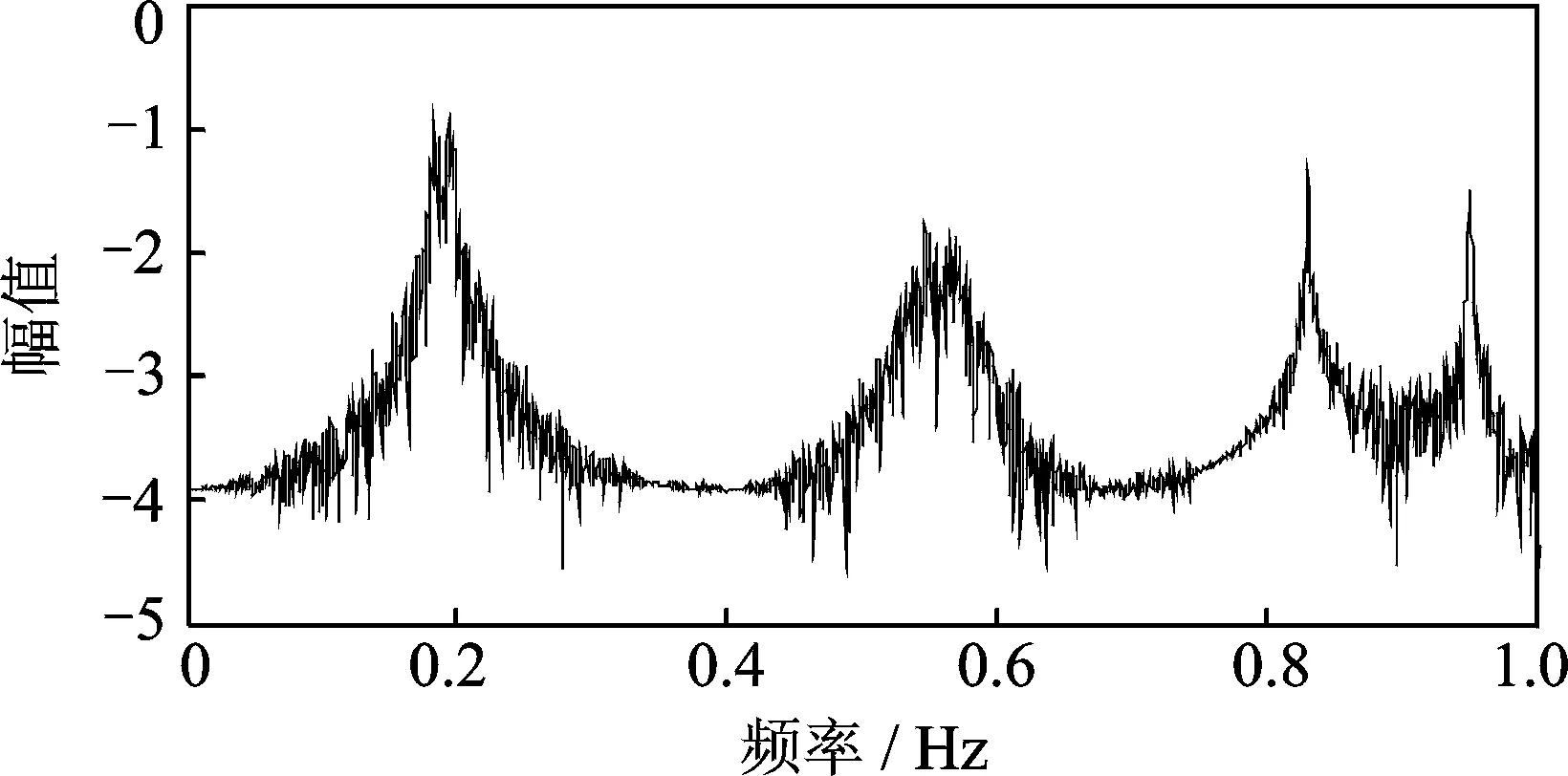
图6 顶层加速度傅里叶谱
Fig.6 The Fourier spectrum of the top level acceleration
从图6的傅里叶谱中可以看出,信号存在密集模态成分,不易找出这些密集模态部分的截止频率。在此,计算顶层加速度响应的自回归功率谱,由式(24)可确定模型阶数p,取150,计算结果如图7所示。同样地,图7中的纵坐标为取以10为底的对数坐标。从图7可以看出,自回归功率谱去除了原有傅里叶谱中的许多虚假频段,得到了比较光滑清晰的谱曲线。可以从自回归功率谱中找到截止频率,截止频率分别为:0.19,0.4,0.56,0.7,0.9 Hz。
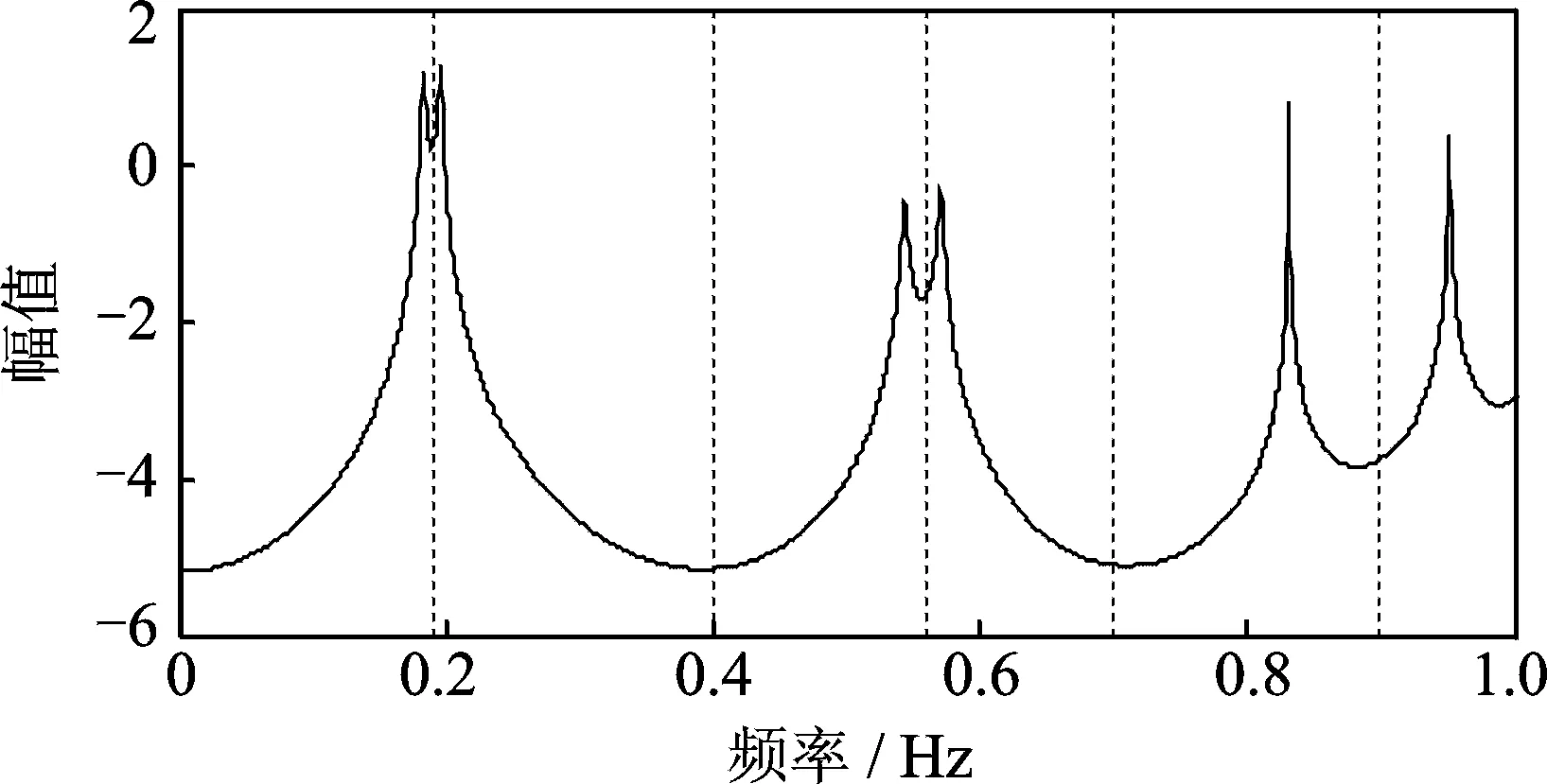
图7 顶层加速度自回归功率谱
Fig.7 The auto-regressive power spectrum of the top level acceleration
4 实验验证
为了验证上述截止频率选取方法的有效性,本文利用采集的江西省吉安赣江公路大桥的环境振动实验数据,对大桥进行了振动响应分析。吉安赣江公路大桥于1995年建成通车,桥梁全长1577 m,东、西引道长3.2 km,主桥桥孔为60 m+4×100 m+60 m预应力混凝土连续箱梁。桥梁设计荷载:汽车-超20级,人群-3.5 kN/m2。该桥主桥上部结构构造为双箱单室连续箱梁,下部结构为V形预应力混凝土墩。左半跨桥共3跨桥梁的环境振动实验的测点布置如图8所示。由于对称性,右半跨桥共3跨桥梁的环境振动实验的测点布置与图8对称。
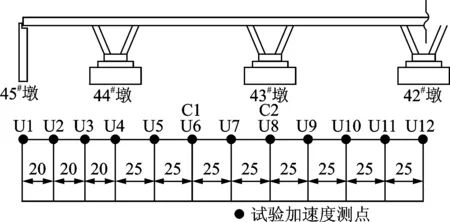
图8 赣江大桥半幅桥的测点布置图(单位:m)Fig.8 The layout of half bridge of Ganjiang Bridge(Unit:m)
选取测点6的一组加速度数据进行分析,其加速度时程如图9所示。图10为测点6加速度响应的傅里叶谱图,为了较为清楚地显示傅里叶谱图,图10的纵坐标为取以10为底的对数坐标。

图9 测点6加速度响应Fig.9 The acceleration of the measured point 6

图10 测点6加速度傅里叶谱
Fig.10 The Fourier spectrum of the acceleration at the measured point 6
从图10的傅里叶谱中难以找出信号分解的截止频率。计算测点6加速度响应自回归功率谱,同样,由式(24)可确定模型阶数p,取85,计算结果如图11所示。图11中的纵坐标为取以10为底的对数坐标。由图11可知,在测点6加速度响应的自回归功率谱中可以清楚地选出截止频率的位置,截止频率分别为:3.5和5.5 Hz,这里只选取了前两阶模态。利用在自回归功率谱中找到的截止频率,对赣江公路大桥测点6的环境振动加速度信号进行扩展离散解析模式分解,分解得到前两阶振动响应如图12所示。

图11 测点6加速度自回归功率谱Fig.11 The auto-regressive power spectrum of the acceleration at the measured point 6
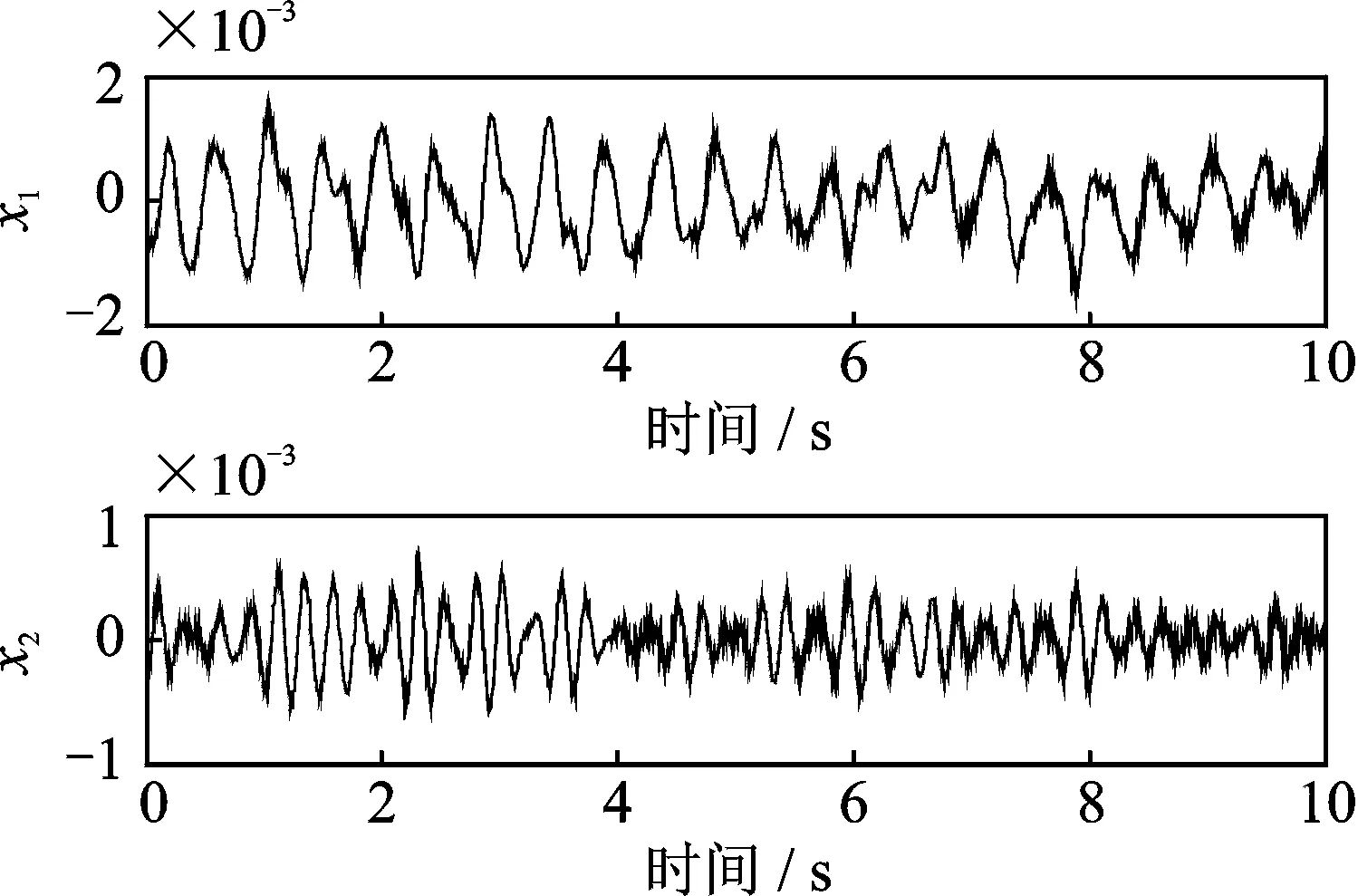
图12 测点前两阶振动响应Fig.12 The first two order vibration response
将该桥的每一个测点同测点6一样进行计算得到每一个测点的前两阶振动响应,然后对该桥进行模态参数识别。实际上,模态参数识别是振动工程理论中的一个重要分支,是研究结构动力特性的一种近代方法。模态是结构的固有振动特性,每个模态具有特定的固有频率、阻尼比和模态振型。模态参数识别主要是通过采集系统的输入信号和输出信号,从而建立系统的数学模型并求解,进而获得系统的动态系统。模态参数识别的基本方法有多种,如频域法、时域法、单自由度法和多自由度法等,其中希尔伯特变换[22]是重要的模态参数识别方法之一。
基于上述论述,对实桥数据作希尔伯特变换处理,得到各测点前两阶振动的瞬时幅值和相位角,再将得到的各测点瞬时幅值取平均,同时结合各相位角的正负可以得到吉安赣江公路大桥的前两阶对最大值归一化的振型,其中图13为获得的1阶竖向振型,图14为获得的2阶竖向振型,由于对称性,图13和14只画出了左半桥3跨桥梁的振型图。

图13 一阶竖向振型Fig.13 The first order vertical mode

图14 二阶竖向振型
Fig.14 The second order vertical mode
5 结 论
论文研究了结构动力响应扩展离散解析模式分解和截止频率选取的优化方法。提出了离散信号分解的两步扩展离散解析模式分解,有效地解决了解析模式分解进行离散信号分解时留有高频残余量的问题。同时,论文为解决离散解析模式分解的截止频率自动化选取,提出了用自回归功率谱代替傅里叶谱选取截止频率的方法,自回归功率谱的谱曲线的峰值清晰且无虚假峰值,可以有效地获得解析模式分解所需的截止频率。论文通过对一模拟的离散信号和对一个具有密集模态的36层框架结构的振动响应信号进行分解,验证了所提方法的有效性。最后,对吉安赣江公路大桥进行环境振动试验,获测了加速度时程数据,利用所提方法对加速度信号进行了有效分解,获得了大桥的前两阶加速度振动响应,利用分解的振动响应,进而识别出了大桥的前两阶振型。主要结论有:
(1)扩展离散解析模式分解是解析模式分解在离散信号处的有效延展,可以解决离散的振动信号分解的误差问题。
(2)利用自回归功率谱代替傅里叶谱在扩展离散解析模式分解中可以有效地获得信号分解的截止频率。
(3)提出的利用自回归功率谱选取振动信号离散解析模式分解截止频率的方法可以对具有密集模态信号或者具有低信噪比的信号,如环境振动信号进行有效分解,通过分解的信号,可以较好地识别结构的振动频率与振型。
[1] 高维成, 刘 伟, 邹经湘. 基于结构振动参数变化的损伤探测方法综述[J]. 振动与冲击, 2004, 23(4):1—7.
Gao Weicheng, Liu Wei, Zou Jingxiang. Damage detection methods based on changes of vibration parameters: A summary review[J]. Journal of Vibration and Shock,2004,23(4):1—7.
[2] 宗周红, 牛 杰, 王 浩. 基于模型确认的结构概率损伤识别方法研究进展[J]. 土木工程学报, 2012,45(08):121—130.
Zong Zhouhong, Niu Jie, Wang Hao. Research progress of structural probabilistic damage identification method based on modal recognition[J].Journal of Civil Engineering, 2012,45(08):121—130.
[3] 伊廷华, 李宏男, 王国新. 基于小波变换的结构模态参数识别[J]. 振动工程学报, 2006, 19(1):51—56.
Ying Tinghua, Li Hongnan, Wang Guoxin.Structure modal parameter identification based on wavelet transform[J].Journal of Vibration Engineering,2006,19(1):51—56.
[4] 焦 莉, 李宏男. 基于数据融合和小波分析的结构损伤诊断[J]. 振动与冲击,2006,25(5):85—88.
Jiao Li, Li Hongnan. Structural damage diagnosis based on data fusion and wavelet analysis[J].Journal of Vibration and Shock,2006,25(5):85—88.
[5] Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[M].The Royal Society,1998.
[6] Huang N E, Shen S S P. Hilbert-Huang Transform and Its Applications[M]. World Scientific,2005.
[7] Wu Z, Huang N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J].Advances in Adaptive Data Analysis,2011,01(01):1—41.
[8] Feldman M. Time-varying vibration decomposition and analysis based on the Hilbert transform[J]. Journal of Sound & Vibration,2006,295(3):518—530.
[9] Feldman M. Hilbert transform methods for nonparametric identification of nonlinear time varying vibration systems[J]. Mechanical Systems & Signal Processing,2014,47(1-2):66—67.
[10] Chen G D, Wang Z C. A signal decomposition theorem with Hilbert transform and its application to narrowband time series with closely spaced frequency components[J]. Mechanical Systems & Signal Processing,2012,28(2):258—279.
[11] 王佐才, 任伟新. 基于解析模式分解的密集工作模态参数识别[J]. 噪声与振动控制,2013,33(6):18—24.
Wang Zuocai, Ren Weixin. The identification of intensive working mode parameters based on analytical mode decomposition[J]. Noise and Vibration Control,2013,33(6):18—24.
[12] Feldman M. A signal decomposition or lowpass filtering with Hilbert transform[J].Mechanical Systems & Signal Processing,2011,25(8):3205—3208.
[13] 王佐才, 任伟新, 邢云斐. 基于解析模式分解的时变与弱非线性结构密集模态参数识别[J].振动与冲击,2014,33(19):1—7.
Wang Zuocai, Ren Weixin, Xing Yunfei. The time-varying and weakly nonlinear structure density parameter identification based on analytical mode decomposition[J]. Journal of Vibration and Shock, 2014,33(19):1—7.
[14] Wang Z C, Chen G D. Analytical mode decomposition of time series with decaying amplitudes and overlapping instantaneous frequencies[J].Smart Materials & Structures,2013,22(9):09503.
[15] Wang Z C, Ren W X, Chen G D. Time-varying linear and nonlinear structural identification with analytical mode decomposition and Hilbert transform[J]. Journal of Structural Engineering,2013,139(12):06013001, 1—5.
[16] 陈建兵, 刘章军, 李 杰. 非线性随机动力系统的概率密度演化分析[J].计算力学学报, 2009, 26(3): 312—317.
Chen J B, Liu Z J, Li J. Probability density evolution analysis of nonlinear dynamical systems[J]. Journal of Computational Mechanics, 2009, 26(3): 312—317.
[17] Lauria D, Pisani C. On Hilbert transform methods for low frequency oscillations detection[J].Iet Generation Transmission & Distributon,2014,8(6):1061—1074.
[18] 陈 宇, 陈怀海, 李赞澄,等. 时变AR模型的一种定阶方法[J]. 振动与冲击,2012,31(8):158—163.
Chen Yu, Chen Huaihai, Li Zancheng, et al. A definite order method of the time-varying AR modal[J]. Journal of Vibration and Shock,2012,31(8):158—163.
[19] 杨书玲, 李艳斌. 基于AR模型的载频测量[J]. 无线电工程, 2006, 36(09):23—25.
Yang Shuling, Li Yanbin. The carrier frequency measurement based on AR model[J]. Journal of Radio Engineering, 2006, 36(09):23—25.
[20] 罗 丰, 段沛沛, 吴顺君. 基于Burg算法的短序列谱估计研究[J]. 西安电子科技大学学报(自然科学版), 2005, 32(5):724—728.
Luo Feng, Duan Peipei, Wu Shunjun. A short sequence spectrum estimation study based on Burg algorithm[J]. Journal of Xi′an University of Electronic Science and Technology(Natural Science),2005,32(5):724—728.
[21] 单东升, 张培强, 李 超. 基于AR模型的功率谱估计[C].全国信号和智能信息处理与应用学术会议论文摘要集.中国,张家界,2012:504—527.
Shan Dongsheng, Zhang Peiqiang, Li Chao. Estimation of power spectrum based on AR model[C].National Signal and Intelligent Information Processing and Application Academic Conference, Zhangjiajie, China, 2012:504—527.
[22] Yang J N, Lei Y, Pan S,et al. System identification of linear structures based on Hilbert-Huang spectral analysis.Part I: Normal modes[J]. Earthquake Engineering and Structural Dynamics,2003,32(10):1443—1467.

