双枝模糊粗集的分解

刘保仓, 刘 畅

(1.黄淮学院 数学与统计学院，河南 驻马店 463000；2.郑州科技学院 财经学院，河南 郑州 450000)

0 引言

文献[1]提出的模糊集理论和文献[2]提出的粗集理论均是研究信息系统中知识的不完全性及不确定性问题，侧重点虽然不同，但二者存在密切的关系.文献[3]把模糊集与粗集进行融合提出模糊粗集，文献[4-7]讨论了其性质和结构.以工程决策与工程控制系统为实际背景，文献[8]提出双枝模糊集，使模糊集理论得到推广.文献[9]把双枝模糊集和粗集进行某些整合提出粗双枝模糊集.文献[10-12]对粗双枝模糊集进行了深入讨论.文[13]提出了双枝模糊粗集并讨论了其性质.在以上研究的基础上，本文提出双枝模糊粗集的截集概念，讨论了双枝模糊粗集的结构，给出相应的分解定理.

为了方便，以下约定：U,X是有限论域；X⊆U，X+,X-,X0分别称作X的上域、下域和界域；S是X上的双枝模糊集，S(x)是x∈X关于S的接吻函数，F(x)是X上的双枝模糊集S的集合，P(x)是经典集合；R是U的一个等价关系，(U,R)是Pawlak近似空间，BF(X)为双枝模糊集.这些概念及记法在文献[4，8]中有详细表述.

1 双枝模糊粗集

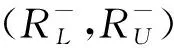
所有定义在X上的下枝模糊粗集记为LFR(X).

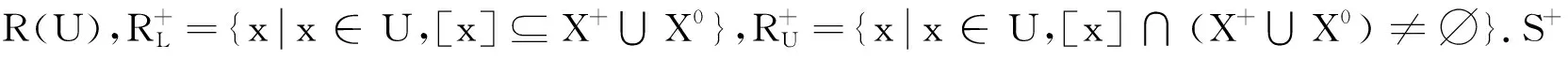
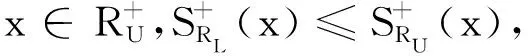
所有定义在X上的上枝模糊粗集记为UFR(X).

定义3[13]设R(U)为粗集之集合,(RL,RU)⊆R(U),RL={x|x∈U,[x]⊆X},RU={x|x∈U,[x]∩X≠∅}.S是X上的一个双枝模糊集,则X中的一个双枝模糊粗集SR=(SRL,SRU)由一对映射给出SRL:RL(x)→[-1,1],SRU:RU(x)→[-1,1],∀x∈X，且∀x∈RU,SRL(x)≤SRU(x).∀x∈RU(x)，称～SR=(～SRL,～SRU)为S的补集，且～SRL(x)=±1-SRU(x),～SRU(x)=±1-SRL(x).

所有定义在X上的双枝模糊粗集记为BFR(X).

2 双枝模糊粗集的分解

(SRL)λ={x||RL(x)|≥|λ|},

(1)

(2)

且

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

定义5 设S∈F(x)，λ∈[-1,1]，规定λS∈F(x)，λS的模糊接吻函数定义为

(λS)(x)=λ∧S(x).

定理1(BFR(X)分解第1定理) 设S∈F(x)为BF(X)，SR=(SRL,SRU)为BFR(X)，则

SR=(SRL,SRU)=

证明(a)设λ∈[-1,0]，∀x∈X-∪X0，由定义4、式(3)和式(5)得：

即

(11)

(b)设λ∈[0,1]，∀x∈X+∪X0，由定义4、式(7)和式(9)得：

(12)

将式(11)和式(12)两式合并得

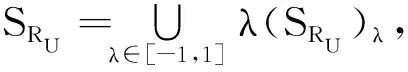
SR=(SRL,SRU)=

证毕.

定理2(BFR(X)分解第2定理) 设S∈F(x)为BF(X)，SR=(SRL,SRU)为BFR(X)，则

SR=(SRL,SRU)=

证明由定义4及式(4)、(6)、(8)、(10)，与定理1证明类似，略.证毕.

定理3(BFR(X)分解第3定理)S∈F(x)为BF(X)，SR=(SRL,SRU)为BFR(X)，且

HRL:[-1,1]P(x)，λHRL(λ)，

HRU:[-1,1]P(x)，λHRU(λ)

满足

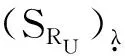
则

SR=(SRL,SRU)=

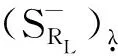
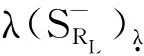
所以由定理1及定理2得

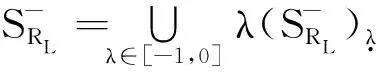
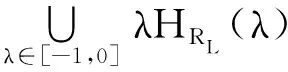
即

(13)

(b)若λ∈[0,1]，与(a)类似可证

(14)

合并式(13)和式(14)得:

同理可证

因此

SR=(SRL,SRU)=

证毕.

定义6 设S∈F(x)，λ∈[-1,1]，规定:λS∈F(x)，λS的模糊接吻函数定义为

(λS)(x)=λ∨S(x).

定理4(BFR(X)分解第4定理) 设S∈F(x)为BF(X)，SR=(SRL,SRU)为BFR(X)，则

SR=(SRL,SRU)=

证明(a)设λ∈[-1,0]，∀x∈X-∪X0，由定义6、式(3)和式(5)得

因此

(15)

(b)设λ∈[0,1]，∀x∈X+∪X0，由定义3、式(7)和式(9)，与(a)的证法类似可得：

(16)

将式(15)和式(16)合并，得

SR=(SRL,SRU)=

证毕.

定理5(BFR(X)分解第5定理) 设S∈F(x)为BF(X)，SR=(SRL,SRU)为BFR(X)，则

SR=(SRL,SRU)=

证明由定义6、式(4)、式(6)、式(8)和式(10)，与定理4证法类似，略.证毕.

定理6(BFR(X)分解第6定理)S∈F(x)是BF(X)，SR=(SRL,SRU)是BFR(X)，且HRL:[-1,1]P(x)，λHRL(λ)，HRU:[-1,1]P(x)，λHRU(λ)满足

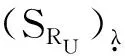
则

SR=(SRL,SRU)=

由定义4～定义6、定理1～定理6得：

推论1 设S∈F(x)是BF(X)，SR=(SRL,SRU)是BFR(X)，若X-=∅，则

推论2 设

(SR)λ=((SRL)λ,(SRU)λ)，

为BFR(X)的λ-截集及λ-强截集，则

推论3 设S∈F(x)是BF(X)，SR=(SRL,SRU)是BFR(X)，若SRL(X)⊆Q⊆[-1,1]，

SRU(X)⊆Q⊆[-1,1]，

SRL(X)={SRL(x)|x∈X}，

SRU(X)={SRU(x)|x∈X}，

则

3 结束语

本文利用双枝模糊粗集的截集概念，讨论了双枝模糊粗集的结构，给出了双枝模糊粗集的分解定理.由讨论知，双枝模糊集与粗集具有紧密的联系，双枝模糊集是模糊粗集的推广.以上讨论，丰富了双枝模糊集和粗集的内涵，为进一步揭示双枝模糊集和粗集的关系打下了一定的基础.