几何模型构造法的解题策略探讨

陈志惠

（漳浦达志中学，福建 漳州 363208）

一、初中生在几何解题中存在的常见问题

学会正确的数学思考、数学构造、数学表达是学生数学素养的重要体现。而学生在解题中存在的问题核心也是这三点。

1.面对试题百思不得其解，是对几何模型不熟悉的体现

几何的基础是基本的几何图形，而基本的几何图形可以构造出各种不同的模型，从而衍生出各式各样的试题。我们在平时的教学过程中，或在辅导学生解题时，只是就题论题，一味解题，而没有及时总结、归类，提炼模型、方法、解题策略，最终可能并不会有太多收获。特别是在遇到模型叠加及综合时，能否可以准确判断出相关模型及问题的切入点，决定了一道试题能否在规定时间内被攻破。只有掌握了各种几何模型的通法解法，才能使我们快速地找到解题思路。

2.不会添加辅助线，往往是对重要关键词不敏感

几何压轴题，往往注重多种几何模型综合、灵活运用。而几何模型的综合，有时并不会完整地展现几何模型，题目中可能只会展现模型中最基础的、关键的一部分图形，因而，这就需要我们能捕捉到这些关键字眼或关键的图形信息，找到显性或隐性的已知条件，并能在大脑中反应出可能的基本几何模型，通过添加辅助线构造出可能的基本几何模型，通过在模型通法中，挑选出正确的做法。

3.解题过程漏洞百出，是因为推理逻辑不清，对模型通法不熟

解题过程容易出现逻辑错误，是因为我们的推理能力不足，逻辑思维混乱，对模型的条件、结论及推理过程不熟，也就是说对图形的数学本质没有深入的认识和理解。在解题教学中，应注重对试题的数学本质，图形的数学本质进行钻研和挖掘，让学生清楚知识的来龙去脉，经历知识的产生、推理、运用过程，注重步骤的规范书写，注重综合法、分析法的综合运用，发展演绎推理能力和逻辑推理，渗透数形结合思想，发展几何直观，养成良好的数学学习习惯。

二、几何模型构造法的解题策略探讨

1.解题策略之“巧用图形的对称性构造对称全等”

数学教材是一切数学教学活动的出发点，深入理解教材对我们的教学有重要的作用。我们在使用数学教材时，不难发现，教材对图形性质的探索，无论是从点、线、面、体的探索，到线段、射线、直线、相交线、平行线的性质探索，或是线段的垂直平分线、角平分线、等腰三角形的性质探索，或是平行四边形、菱形、矩形、正方形、圆的性质探索，无不是从图形的对称性入手的，通过折纸、画图活动，让学生经历观察、猜想，测量、计算、推理、验证等一系列探索过程，从而培养学生的几何直观能力，认识几何模型，达到对图形数学本质的认识，形成能力和思维。因此，对称性是探索图形性质的重要方法，也是解决图形问题的重要思路。

（1）巧用图形对称性解题之“角平分线模型”

角平分线模型最主要的解题策略是构造对称全等，利用图形的对称性、全等的性质进行问题的转化、推理、计算，是初中数学非常重要的解题方法，而常见的对称构造法有以下几种情况：

例题1：已知：AD平分∠BAC，BD⊥AD. 求证：∠ABD= ∠DBC+∠C （如图1）

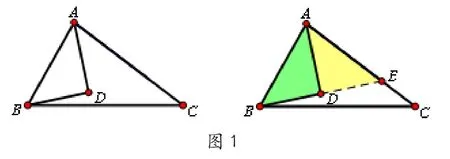
解题策略是利用角平分线的对称性，当角平分线遇上垂直时，可以顺延，得到等腰三角形。即构造对称全等解决问题。

例题1变式1：已知：OP平分∠MON，PA=PB. 求证：∠OAP+∠OBP=180°（如图2）

解题策略是利用角平分线的对称性，角平分线上的点向角的两边作垂线，构造对称全等解决问题。

例题1变式2：ΔABC中，AD平分∠BAC，∠C=2∠B. 求证：AB=AC+CD（如图3）

解题策略是利用角平分线的对称性，当证明线段的长度关系时，截长补短法是重要的解题思路，问题的本质也是构造对称全等。

从上例可以看出，当题目中有直接给出或隐含的角平分线条件时，除了构成等角外，还应特别注意从角平分线两个方面的功能来分析和认识图形：① 以角平分线为轴，构成怎样的对称图形？② 以角平分线和平行线结合，构成怎样的等腰三角形？思考若以这样的功能作指导，大都会找到恰当的解决方法。

（2）巧用图形对称性解题之“将军饮马模型”

最值问题、最佳方案是数学思考的一个重要方面，它为生活带来便利，体现数学与生活的密切联系。将军饮马模型是数学最值问题中的一个重要模型，它蕴含着几何直观、空间观念的培养；转化、化归思想的渗透；对称性解题策略的运用；几何推理与计算在实际问题中的运用等，对称构造是将军饮马模型的主要解题策略。

如图，A、B是直线l外的两个定点，在直线l上求作点P，使PA+PB路程最短。

例题2：如图4，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使 PD＋PE 的和最小，求这个最小值。

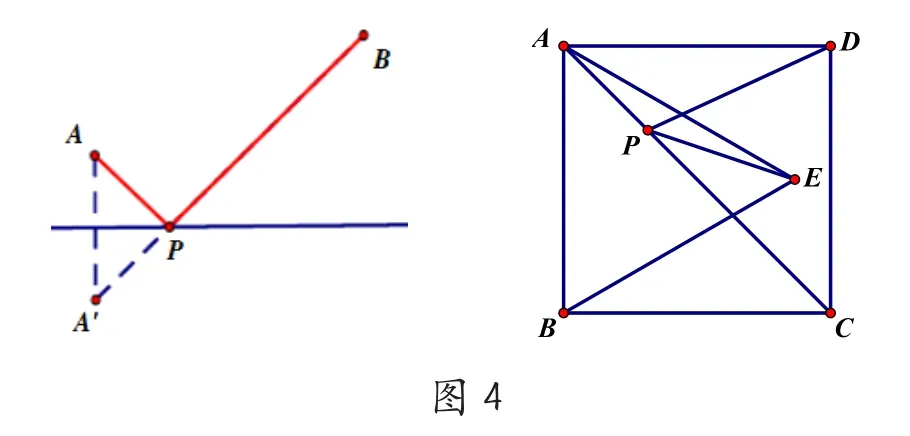
将军饮马题型的解题策略是利用轴对称的性质作对称点，原理是利用三角形的两边之和大于第三边，解题技巧是化折为直，即口诀法：分清动定点，动点成直线，定点来照镜，隔线把点连。

2.解题策略之“几何模型构造法，运用模型通法解题”

“一题多解，解法优化；一题多变，变中求同；多题一法，同模通法”是数学解题与习题教学中重要的教学方法，也是学生学习的方法。对各个数学知识模块，进行这三个维度的探究教学，有益于学生的数学思维能力的培养。

（1）巧用几何模型一题多解，多解归一

一题多解可以帮助学生开阔思路，把学过的知识和方法融会贯通，可大大提升分析问题和解决问题的能力；可以培养学生灵活、敏捷的思维能力，让学生学会对问题进行多角度、多层次的分析，达到对问题的全面理解，进而迅速准确地解决问题；可以培养学生的发散性思维及联想能力，学会用不同的知识解决同一个问题，达到对多种知识的融会贯通。

例题3：正方形ABCD中，CD=2，点P在以AC为直径的半圆上，AP=1，∠DPC=45°，求点D到PC的距离。（如图5）

解法1：利用几何计算三大法宝之一“勾股定理”列方程求解。解题策略：遇垂线，求长度，勾股定理少不了！解法2：利用几何计算三大法宝之二“相似列比例式”求解。解题策略：求长度，构相似，隐藏信息是关键！解法3：利用几何计算三大法宝之三“锐角三角函数”求解。解题策略：求长度，找角度，三角函数来帮忙！解法4：手拉手，现全等。解题策略：拨开迷雾，图形看本质，手拉手，现全等！解法5：对角互补，四点共圆或旋转解题。解题策略：遇等边，共顶点，全等旋转是关键！解法6：相似变换，一转成双。解题策略：一对共顶点的相似三角形绕公共顶点旋转可得另一对相似三角形，简称：“一转成双”，用旋转变换构造相似形三角形，是把分散的边角条件集中到特殊图形中，以使其产生联系。

例题4：正方形ABCD的边长为4，P是AC上的一个动点（不与A、C重合），连接BP，将BP绕点B顺时针旋转90o到BM，连接MP，并延长交BC点E，交AD（或AD延长线）于点F.（如图6）

（1）连接CM，证明：AP=CM；

（2）设AP=x，CE=y，试写出y关于x的函数关系式；

（3）猜想PF与EM的数量关系，并证明你的结论．

拨开迷雾，图形看本质。第（1）题是手拉手模型，手拉手，现全等。第（2）题是一线三等角模型，问题的本质是相似。第（3）题解法多样化，可以利用不同的几何模型通法，从而达到一题多解。解法1：截长法构造全等。解法2：补短法构造全等。解法3：角平分线构造对称全等。解法4：手拉手和角平分线结合构造全等。解法5：利用手拉手和对角互补模型。解法6：利用三垂直模型全等。解法7：三垂直模型和平行线分线段成比例相结合。解法8：手拉手和角平分线构造对称全等。通过一题多解，把学过的知识和方法融会贯通，从而提升对试题本质的认识，提高解题能力。

（2）一题多变，变中求同；多题一法，同模通法

课本例题、习题为学生开拓思维提供了丰富的资料，是教师开展变式教学的重要资源，其思维方式的典型性、解题过程中的示范性是课外习题不能比拟的。课本例题、习题是许多中考题的原始来源，例题、习题的拓展常常成为中考的考点。我们可以通过很多途径对课本的例题、习题进行变式。如：改变条件、改变结论、改变数据、改变图形；条件引申、结论拓展；条件开放或结论开放，或条件、结论同时开放等。

例题5：如图，四边形ABCD中，∠ABC=∠A DC=90o，BD平分∠ABC，∠DCB=60o，AB+BC=8，求AC的长。（如图7）

变式一：改变图形背景。如图，⊙O的直径AB为10cm,弦AC为6cm，∠ACB的平分线交⊙O于D。（1）求BC的长；（2）求AD,BD的长。

变式二：保留结论，更换条件。如图，⊙O的 弦AB长10cm,∠ADB=90°， 弦AC长6cm，AD=BD（1）求BC的长；（2）求AD,BD的长。

变式三：保留条件，结论拓展。如图，⊙O的直径AB为10cm,弦AC为6cm，∠ACB的平分线交⊙O于D。求CD的长。

变式四：把等腰直角三角形换成等边三角形。

变式五：把等边三角形换成正方形。

变式六：把正方形换成正多边形。

认识和体会数学是一个整体，变式例题（习题）教学应该突出变式中的共性，切忌就题论题，应引导归纳总结，通过特殊去发现一般规律，能“解一题，懂一法，会一类，通一片”。

3.解题策略之“联想构造法：运用中点模型解题”

中点是几何解题中常常遇到的，特别是三角形的中点、中线、中位线及直角三角形斜边上的中线等是高频考点，是中考的必考内容。遇到中点，我们应从哪些方面进行思考呢？

以直角三角形斜边上的中点为例，请看例6、例7，寻求中点模型的构造法。

例题6：□ABCD中，AB=3，BC=4，E为□AB CD外一点，∠AEC=∠BED=90o。（如图8）

（1）求□ABCD的面积。

（2）求四边形ABCE的面积的最大值。

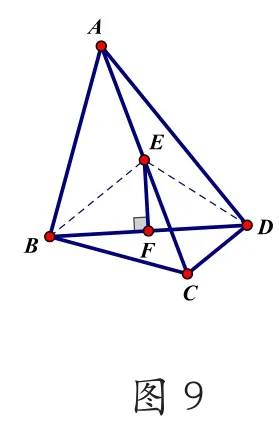
例题6变式：在Rt△ABC和Rt△ADC中，∠ABC=∠ADC=90o，E、F分别为AC和BD的中点。（如图9）

（1）求证：EF⊥BD。

（2）若∠BAD=45o，求AC：EF的值。

例题7：已知：AD、AE分别是△ABC的高和中线． （如图10）

（1）若AC=2DE，求证： ∠C=2∠B。

（2）若∠C=2∠B ，求证：AC=2DE。

例题6由两个直角联想到直角三角形，想到连接对角线，而矩形使得两条斜边有了联系，因此，共中线等斜边是本题最大的特点，也是需要学生发现的地方；例6变式和例6区别在于共斜边而得到等中线，和例6是条件结论互换，解题策略为：（1）共中线、则等斜边；（2）共斜边，则等中线。例7由已知中点，需要联想构造，使高和中线产生联系，从而使问题得到解决；（3）知中点，作中点，中线和中位线完美结合。一个中点不够，再构造一个中点，使分散的已知条件集中。