拉普拉斯算子多项式第二特征值估计的不等式
杨晓华,钱椿林
(苏州市职业大学 数理部,江苏 苏州 215104)
设Ω⊆Rm(m≥2)是一个有界区域,Ω的边界∂Ω是逐片光滑的,考虑如下的拉普拉斯算子多项式第二特征值λ2的上界估计的问题

式中:ν是区域Ω的边界∂Ω的外法向量;l和r是非负整数且l≥2r;P(t)=al-rtl+al-r-1tl-1+…+a1tr+1,常数al-r=1,当i=1,2,…,l-r-1时,常数ai≥0;Q(t)=brtr+br-1tr-1+…+b1t,常数br=1,当i=1,2,…,r-1时,常数bi≥0。
关于此类第二特征值估计已有结果[1-7]。在本文中,将文献[8]与[9]中的常微分方程的第二特征值估计推广到拉普拉斯算子更广泛的一类问题,即问题(1)。
1 主要结果
定理1 设λ1,λ2是问题(1)的第一、第二特征值,且0<λ1≤λ2,则有

式中r1={j│b1=b2=…=bj-1=0,bj≠0}。对于给定l与r选正整数参数σ使得式(2)的右端达到最小值,且r≤σ≤l-r。
注2 在式(1)中,取r=r1,ai=0(i=1,2,…,l-r-1)与bi=0(i=1,2,…,r-1),则式(2)变为,此结果是文献[6]中的定理1。在文献[5]中,取s=l,ai1i2…il(x) = 1(i1,i2,…,il=1,2,…,m),r=1,bii(x)=1(i=1,2,…,m),与bij(x)=0 (i≠j),此结果是文献[5]中的定理1.1。
注3 在式(1)中,取bi=0(i=1,2,…,r-1),则式(2) 变为

在文献[7]中,取 ai1i2…is(x)=as-r(s=r+1,r+2,…,l;i1,i2,…,is=1,2,…,m),t=l与r=rt,式(3)是文献[7]中的定理2。因此,本文的结果是文献[1]-[7]的推广。
2 定理的证明
假设

式中:k=1,2,…,m;x=(x1,x2,…,xm);hk是一个实常数,且

设λ1是问题(1)的第一特征值,相应于λ1的特征函数为u,为简便起见,用∫替代∫Ω,且满足

利用分部积分,得

由式(4)知,φk与u正交,k=1,2,…,m,得

利用Rayleigh定理,有

计算得

利用分部积分,容易得

利用式(7)和式(8),计算得

引理1 设u是问题(1)所对应第一特征值λ1的特征函数,则

证明 ①利用数学归纳法,容易证明

利用式(1)与式(5),有

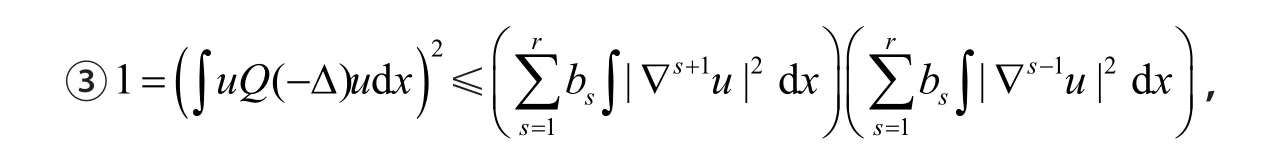
因为l≥2r,所以r≤σ≤l-r。利用①与②,得到

引理2 设u是问题(1)所对应第一特征值λ1的特征函数,则

证明 利用分部积分,容易证明。
引理3 设λ1是问题(1)的第一特征值,则

式中:r1={j│b1=b2=…=bj-1=0,bj≠0};正整数σ=r,r+1,…,l-r。证明 利用 ϕk=( xk- hk) u、引理2②和引理1③,有

类似地得

结合式 (13) 和式 (14) ,有

引理4 设λ1是问题(1)的第一特征值,则
式中:r1={j│b1=b2=…=bj-1=0,bj≠0};σ=r,r+1,…,l-r。
证明 利用引理2②,得

利用式(15)、分部积分、引理1②和Schwarz不等式,有

因此引理4成立。
定理1的证明 利用引理3、引理4和式(10),容易证明。
3 结论
本文利用变分法、Rayleigh定理、分部积分、Schwartz不等式和Young不等式等估计方法与技巧,考虑拉普拉斯算子多项式的第二特征值上界估计,获得了用第一特征值来估计第二特征值的上界的不等式,上界与区域的几何度量无关,很多结果都是本文的特例。

