对一类抛物线考题的多向探究
☉浙江省慈溪市浒山中学 岑孟庆
对一些典型题目需要进行深度“思考”与“二次创作”,挖掘出所潜在的教育功能、拓展功能和应用功能,使考生做一道题会一类题、会一串题,对于提高考生举一反三、触类旁通的数学素养是十分有意义的事情.下面以一道抛物线模考题为例加以说明.
一、考题呈现
例1已知抛物线C:y2=2x和点P(2,2),A、B是C上异于点P的两点,直线PA、PB的斜率kPA,kPB满足kPA+kPB=2,则直线AB过定点( ).
A.(1,0)B.(-1,0)C.(0,-1)D.(0,0)

所以直线AB过定点(0,-1).故选C.
二、结论探究
结论1:P是抛物线C:y2=2px(p>0)上一定点,A,B是C上异于P的两点,直线PA,PB的斜率kPA,kPB满足kPA+kPB=λ(λ为常数,且λ≠0),且直线AB的斜率存在,则直线AB过定点


应用此结论对于“过抛物线C:y2=2px(p>0)上一定点P(x0,y0)的两条直线PA,PB,与抛物线C交于A,B两点,若直线PA,PB的斜率kPA,kPB之和为非零定值,则直线AB过定点”的一类问题便迎刃而解了.
三、纵向思考
上述各结论中,均有条件“λ≠0”,现在我们感兴趣的是若λ=0会有什么样的情形呢?
例2 已知抛物线C:y2=2x和点P(2,2),A、B是C上异于点P的两点,直线PA、PB的斜率kPA,kPB满足kPA+kPB=0,则直线AB的斜率为( ).

结论2:P是抛物线C:y2=2px(p>0)上一定点,A,B是C上异于P的两点,直线PA,PB的斜率kPA,kPB满足kPA+kPB=0,则直线AB的斜率为定值
四、变向思考
上面研究的都是“斜率之和为定值”的情况,若将条件中的“之和”改为“之积”,是否也能出现定点结论呢?答案也是肯定的!
例3已知抛物线C:y2=2x和点P(2,2),A、B是C上异于点P的两点,直线PA、PB的斜率kPA,kPB满足kPA·kPB=2,则直线AB过定点( ).

五、类比思考
对于抛物线“斜率之和为非零定值”这一类试题可由上述的结论解决,那么对于椭圆、双曲线也常有类似的试题出现,那么是否也有一般的结论呢?答案是肯定的!
例4已知椭圆)中恰有三点在椭圆C上.
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点,若直线P2A与直线P2B的斜率的和为-1,证明:l过定点.
解析:(1)由于P3,P4两点关于y轴对称,所以由题设知C必经过P3,P4两点.
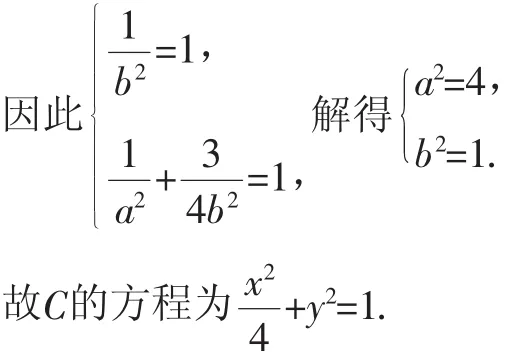
(2)设直线P2A与直线P2B的斜率分别为k1,k2,如果直线l与x轴垂直,设l:x=t,由题设可知t≠0,且|t|<2,可得解得t=2,不符合题意.
由题设可知Δ=16(4k2-m2+1)>0.


