高中数学核心素养导向的学生直观想象能力培养策略探析
——以平面向量为例

陈琼琪

（浙江省严州中学梅城校区，浙江杭州 311604）

1 提出问题

在2017浙江高考数学15题中，考察的是平面向量问题，该问题可以从代数角度解决，也可以从几何角度解决，充分体现了浙江高考数学向量问题命题一贯的风格。题目及解法如下：

2 理论依据

2.1 高中数学核心素养的要求

高中数学核心素养下的直观想象是指借助几何直观和空间想象感知事物的形态与变化，利用图形理解和解决数学问题的过程。主要包括：借助空间认识事物的位置关系、形态变化与运动规律；利用图形描述、分析数学问题；建立形与数的联系；构建数学问题的直观模型，探索解决问题的思路。直观想象是发现和提出数学问题、分析和解决数学问题的重要手段，是探索和形成论证思路、进行逻辑推理、构建抽象结构的思维基础。在直观想象核心素养的形成过程中，学生能够进一步发展几何直观和空间想象能力，增强运用图形和空间想象思考问题的意识，提升数形结合的能力。

2.2 数学大家的经验启示

华罗庚先生说过：“数形本是相倚依，焉能分作两边飞？数缺形时少直观，形少数时难入微，数形结合百般好，割离分家万事休。几何代数统一体，永远联系莫分离。”可见，数形结合的思想在数学中的地位，“数缺形时少直观”说明直观想象能力能使数学问题更直观形象，即把数学与几何图形相结合，化繁为简，化抽象为具体，直观快速地抓住问题的本质与要害，可使解题起到事半功倍的效果。

古希腊数学家欧几里得所著的《几何原本》是一部不朽之作，集整个古希腊数学成果和精神于一书，使几何学变成一座建立在逻辑推理基础上的不朽丰碑。《几何原本》的诞生，标志着几何学已成为一个有着比较严密的理论系统和科学方法的学科。而《几何原本》是在古埃及、古巴比伦时期的“直观几何”的基础上发展起来的。

因此，我们发现，数学问题的发现、分析和解决借助几何形象，运用直观想象能力和数形结合的数学思想方法，使得抽象问题具体化，代数问题几何化。在解决平面向量问题时，我们也可以运用平面向量的几何意义，使得向量问题几何化，从“形”的角度理解向量，养成主动想图、作图和用图思考的习惯，“看”出思路，“看”出简洁。

3 学生直观想象能力的培养策略

从2004年浙江省自主命题以来，向量试题就呈现出鲜明的特点：具有极强的数学味和突出的几何背景，既可以考查向量的代数运算，也能通过对几何背景的透视，抓住向量本质，简化解题思路。在高考中“快狠准”地解决向量问题，几何性质的恰当运用起着至关重要的作用。

3.1 平面向量的模长——距离

向量的模即向量的大小，也即为表示向量的有向线段的长度。向量的加减运算，有平行四边形法则和三角形法则， 常用的+和-即为平行四边形的两条对角线，体现了向量的加减运算的几何意义。向量-通过三角形法则可知，可表示为从|+|的终点指向的终点的有向线段，故|-|即为两个终点间的距离。而加法和减法互为逆运算，同理|+|也可理解为两个终点间的距离。 若当向量和中有一个向量的模长确定时，|+|和|-|可以理解为一个定 点到一个动点间距离的问题。即

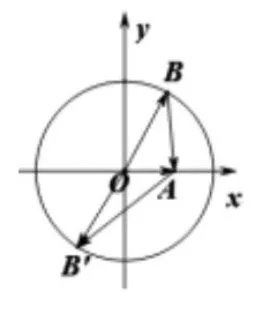
图1

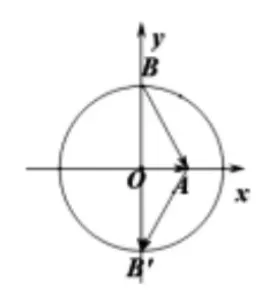
图2

故当B，B'在x轴上左右端点时，取得最小值4（三角形两边之和大于第三边），当如图2位置时，取得最大值

解析：用数形结合方法求解，作正方形OACB，连对角线 AB，则向量等于向量(D 为对角线AB上一点），向量等于向量(E 为OB 边上一点，EB=10），OD＝DC， 所以等于 ED+DC，由几何意义可知 ED+DC的最小值为EC的值，即等于26。故正确答案为B。

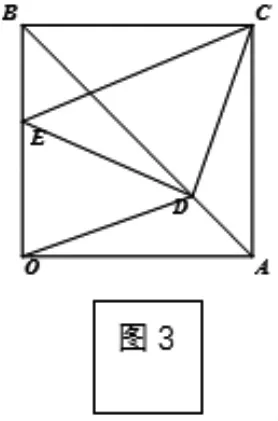
图3

3.2 平面向量的模长——圆

向量的模即向量的大小，也即为表示向量的有向线段的长度。当向量的模确定时，该向量可以用起点在坐标原点，终点在以坐标原点为圆心以向量的模长为半径的圆上的有向线段表示，从而将有关模长问题转化为与圆相关的几何问题，结合直观想象能力，快速解题。

图4

3.3 平面向量的模长——椭圆

此类转化方法建立在前两种转化方法的基础之上，但又胜于前两种转化方法，它的巧妙之处在于将椭圆的几何性质恰到好处地融合到解法中，将|+|+|-|理解为椭圆内的点到两焦点的距离之和，因此通过椭圆的几何性质及三角不等式，很快可以得到，当三点共线时取得最小值，当终点在椭圆上（即短轴端点）时取得最大值，最大值为椭圆的长轴长。

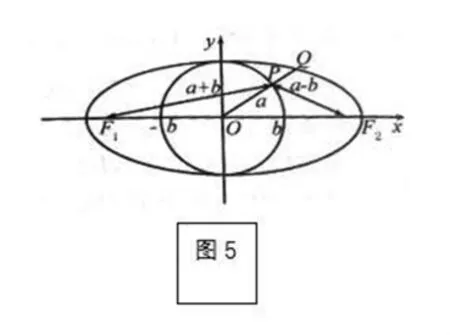
图5

则 F1，F2以为焦点，2||为短轴构成椭圆.

当 F1，P，F2三点共线时等号成立，所以的最小值是4.

4 结语

该文仅通过平面向量问题对培养直观想象能力的初步探讨。数学核心素养的形成不是一项即时性的活动，而是在数学学习中不断积累，不断思考探索，从而形成质变的过程。在日常教学中，重视向量以及向量的模长、向量的运算等的几何意义，从日常教学中点滴渗透几何性质，强化学生的想图、作图和用图的能力，让学生形成直观想象的思维习惯和思维能力，不仅有助于向量问题的解决，直观想象能力在很多数学问题中都能发挥重要作用。