一类带有控制器失效的切换系统的模型参考自适应律的设计
罗俊玉,金朝永,陆诗敏
(广东工业大学应用数学学院,广东广州510520)
在控制切换系统实际运行过程中,由于系统的执行器受各种非人为因素的影响,往往会发生故障,从而导致系统的整体性能下降。针对这种情况,建立一个误差系统,设计系统控制器的自适应律,使其满足在出现执行器失效时,系统仍然保持稳定且达到一定的性能指标,这是一个值得深入研究的问题。而今现有的研究结果,主要是通过给自适应执行器设计补偿控制器来解决带有执行器失效的控制系统的稳定性问题[1-5]。基于这方面的探索,先假设当执行器只有一部分不能正常工作,剩下的部分执行器能继续正常工作去实现目标控制。可大多数时候,这种假设是不能被满足的。比如,当系统为单输入系统时,只具备单独的执行器,所以上述假设明显不成立。因而我们必须去寻找新的方法,处理此类相关的问题。除此之外,在一些特定的情况下,让执行器在尽可能短的时间里停止运作是必然的[6]。由于现有的控制方法还不能很好地解决此类执行器失效时所留下的弊端,故研究如何设计带有执行器失效在有限时间内短暂失效的自适应控制器,无论在理论上还是实际应用中都能保证系统性能的稳定,就具有很重要的实际意义。
1 问题提出
首先考虑如下一类非切换系统

其中,x(t)∈Rn和 u(t)∈Rm分别为系统状态和控制输入,A∈Rn×n和 B∈Rn×m分别为具有未知参数的矩阵。
参考模型为

其中,Am∈Rn×n为Hurwitz常矩阵,Bm∈Rn×m且(Am,Bm)是可控的,r(t)∈RM为持续激励信号,xm(t)为参考模型的状态。
一般情况下,通过自适应控制器 u(t)的设计,使得 x(t)能够渐近跟踪 xm(t),即状态跟踪误差 e(t)=x(t)-xm(t),满足。然而,在实际的系统控制运行中,由于受一些非人为因素的影响,导致所有执行器失效而控制器传递信息失败,在控制器传递信息失败的相应时间段内,系统(1)为开环状态,即B=0n×m。在这种情况下,可以用如下切换系统来代替带有执行器失效的系统(1)

其中,σ(t):[0,+∞)→M={1,2},B1=B,B2=0n×m。当 σ=1 时,激活正常子系统,即系统(1)执行器正常运行,当σ=2时,激活失效子系统,即系统(1)中全部执行器失效。
定义1对∀T1,T2∈C,满足T2>T1≥0,定义Nf(T1,T2)为在时间段[T1,T2)上全部执行器失效的次数,定义Ff(T1,T2)=Nf(T1,T2)(/T2-T1)为在时间段[T1,T2)上的全部执行器失效的频率。
定义2对∀T1,T2∈C,满足T2>T1≥0,定义T+(T1,T2)为在时间段[T1,T2)上全部执行器失效的时间,定义T+(T1,T2)(/T2-T1)为在时间段[T1,T2)上全部执行器失效时间比。
假设1[7]存在常矩阵及非奇异常矩阵,使得下式(4)成立

假设2[7]存在常矩阵 S∈Rm×m,使得是正定矩阵,即

假设3[7]系统(1)中全部执行器失效的最大时间间隔为Ts。
最后,给出本文的研究问题:考虑系统的全部执行器在同一时间里同时失效,并且在相对短的时间里又一起恢复正常运作,则此时针对给定的控制器,设计相应的自适应律,使得系统(1)的状态x(t)能够跟踪参考模型(2)的状态xm(t)。
2 执行器失效情况下的自适应控制器的设计
当σ=1时,正常子系统即切换系统(3)的正常子系统被激活,开始工作,此时,给定如下控制器[8]

由式(1)、(2)、(6)一起构成的闭环系统为
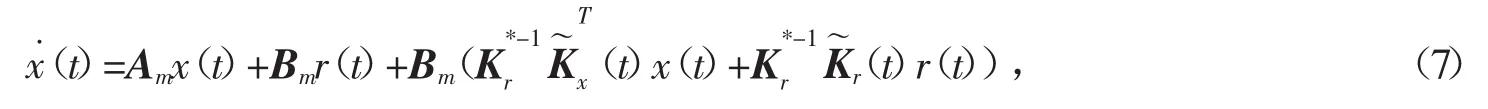
3 自适应律的设计方案
由式(2)、(6)、(7),得执行器被激活(σ=1时)的误差为
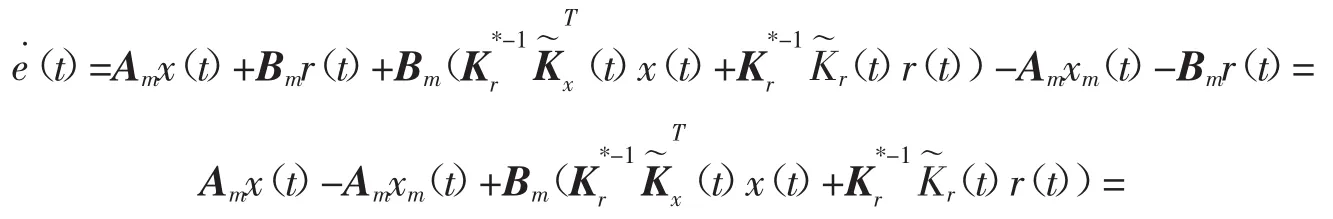
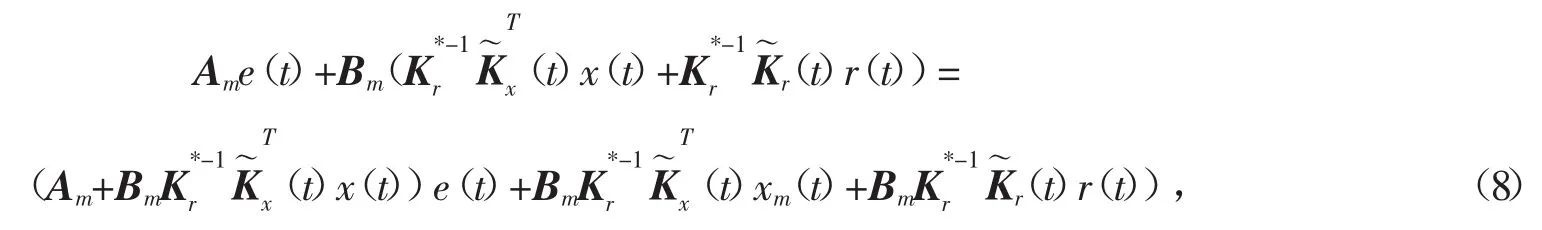
对式(8),设计自适应律为
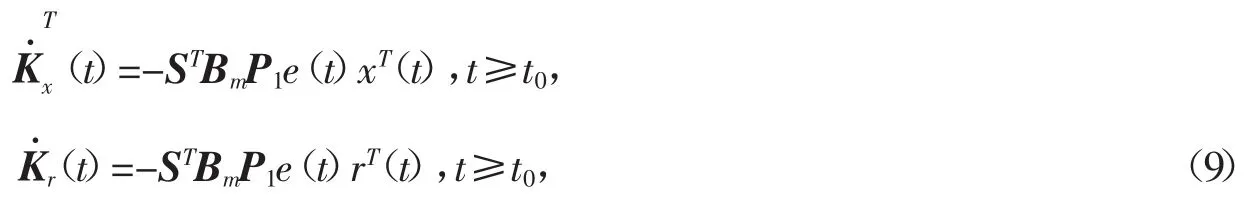
其中,S满足假设2,P1是满足不等式的正定矩阵。
考虑执行器全部失效的情况(σ=2时),由式(1)可得失效误差系统为

此时,设计自适应律为

定理1当自适应律(9)适用于切换系统(3)的正常子系统(σ=1时)和模型参考系统(2),在给定的执行器(6)的反馈控制下,其状态跟踪误差e(t)的轨迹是指数下降的,即
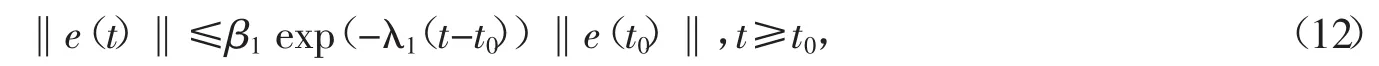
其中,β1≥1,λ1>0,且有。
证明选取如下的Lyapunov函数[9]
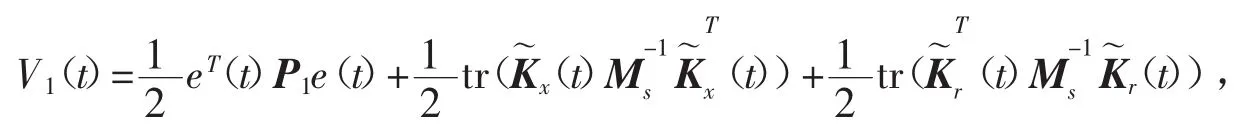
对式V1(t)沿着时间t取导数,得
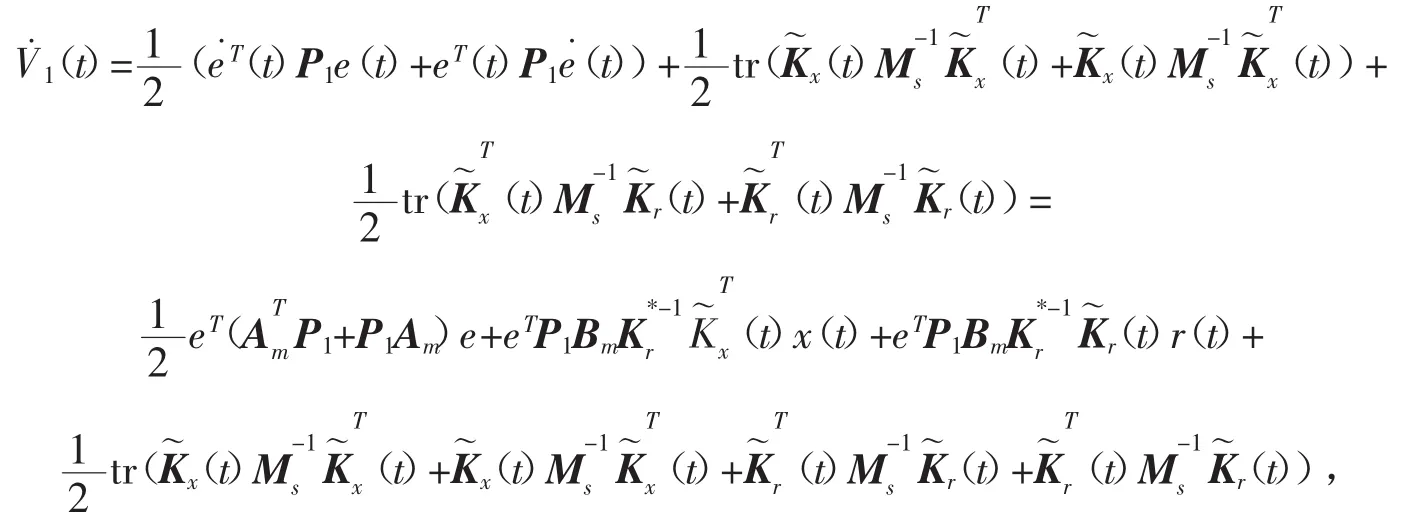
依据矩阵的迹的性质
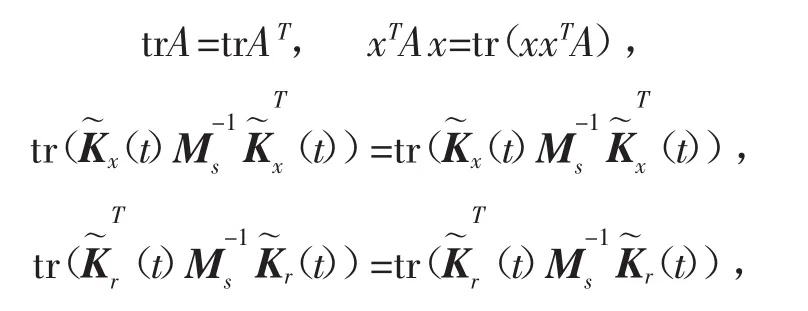
可得

令上式后两项为零,得
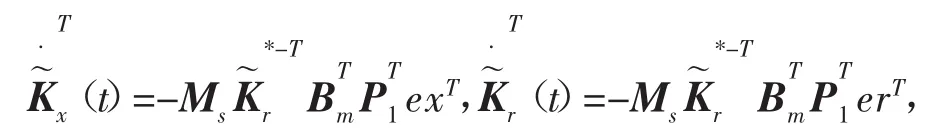
而
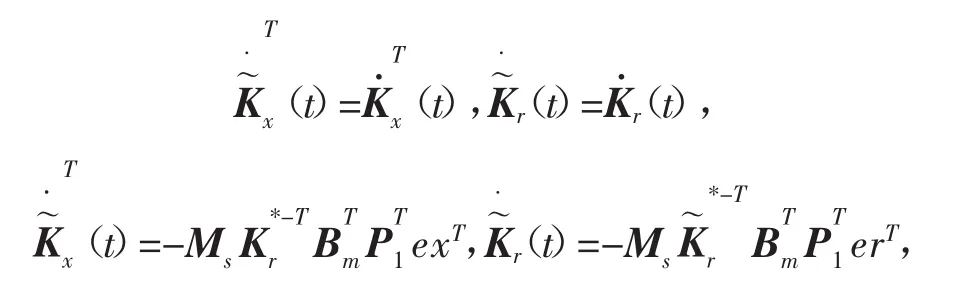
又由假设2,得
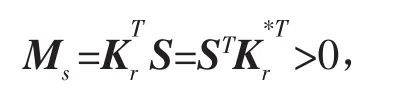
故,设计自适应律为
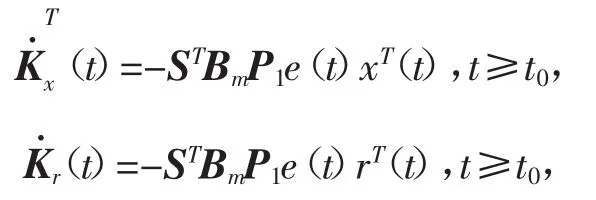
其中,S满足假设2,P1是满足不等式的正定矩阵。
故可得
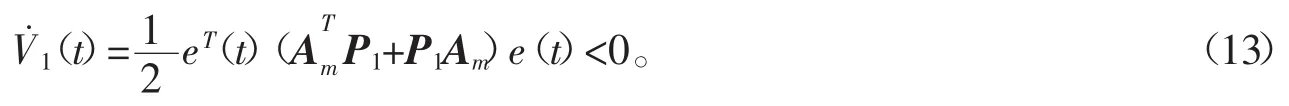
由于(rt)是持续激励信号,且(Am,Bm)是可控的,根据文献[10]可知和φm(t)≜[xT(t),r(t)]是持续激励信号,并通过式(13)不难看出,正常误差系统(8)的状态跟踪误差e(t)的轨迹是指数下降的,即
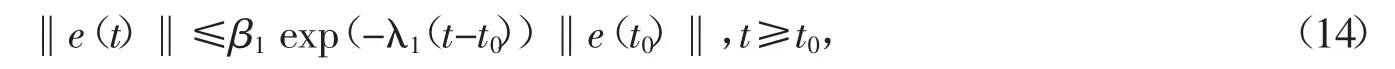
其中,β1≥1,λ1>0,证毕。
考虑执行器全部失效的情况(σ=2时),控制器参数Kx(t)和Kr(t)不影响状态跟踪误差e(t),在这种情况下,通过自适应律(11)使得Kx(t)和Kr(t)的值保持不变;当执行器恢复正常工作时,使自适应律(9)对控制器参数Kx(t)和Kr(t)进行更新。
4 误差系统的实用稳定性分析
根据式(8)、(9),得到式(10)、(11)带执行器失效的误差切换系统为

设计切换自适应律为
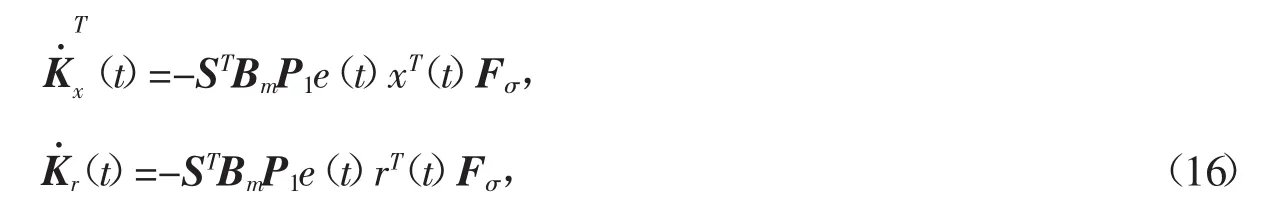
其中,F11=In×n,F12=0n×m,F21=Im×m,F22=0m×m。当 σ=1 时,激活了第 1 个子系统,系统(1)的执行器全部正常工作,当σ=2时,激活了第2个子系统,系统(1)的执行器均暂时失效。
定义3考虑系统(15),对给定常数r*>0,若存在切换信号σ(t)和常数T*=T*(e(t0),r*)≥0,使得对t≥t0+T*,有 e(t:t0,e(t0))∈S(r*)≜{e│‖e‖≤r*}成立,此时,称系统(15)(相应于 r*)是全局实用稳定的。
引理1[7]考虑失效误差系统(10),对∀r0>0,令 S(r0)={e│‖e‖≤r0},如果 e(t0)∈Rn/S(r0),那么∃λ2>0 和 β2≥1,使得如下不等式成立

定理2考虑误差切换系统(15),假设参考输入(rt)是持续激励信号,并且(Am,Bm)是可控的。对于任意偶数 k 及 t<tk,如果切换信号 σ(t)满足:
(a)对 λ*∈(0,λ1),有下面不等式

(b)对 λ∈(0,λ*),有下面不等式

那么,对任意r0>0,存在r*,使得误差系统(15)是全局实用稳定的。
证明对任意的r0>0,令,其中,Λ 满足 Λ≥‖(A-Am)xm(t)-Bmr(t)‖。对于任意的状态跟踪误差初始值e(t0)∈Rn,证明若切换信号σ(t)满足条件(a):(c)时,存在T*=T*(e(t0),r*)≥0,使得当t≥t0+T*时,有

(1)先证明状态跟踪误差e(t)轨迹的吸引性。
考虑 e(tk)∈Rn/S(r0)的情形。对任意偶数 k,当 t>tk时,存在 j∈{k,k+2,k+4,…},使得 t∈[tj,tj+1)或者 t∈[tj+1,tj+2)成立。
当 t∈[tj,tj+1)时,由式(14)和式(17)得
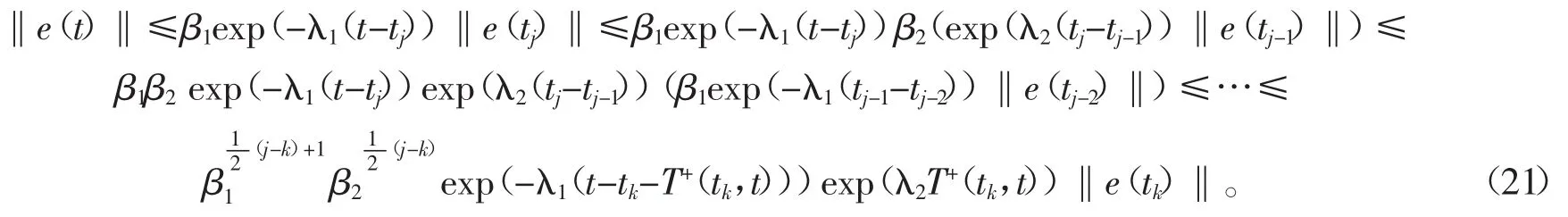
当 t∈[tj+1,tj+2)时,基于同样的方法,由式(14)和式(17)得

根据定义2,当t∈[tj,tj+1)时,有成立,当t∈[tj+1,tj+2)时,有成立。所以,当 t∈[tj,tj+2)时,由式(21)和式(22)得
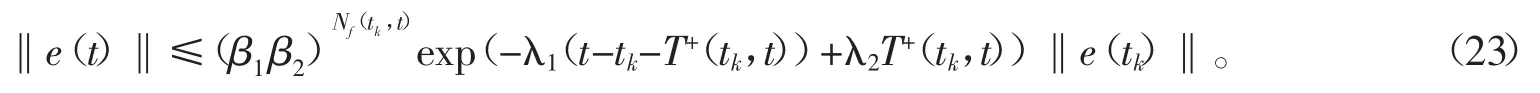
由式(18)得
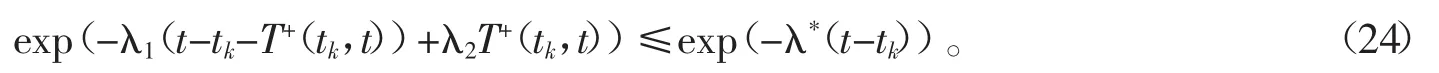
根据式(19)和定义1,有下面不等式成立
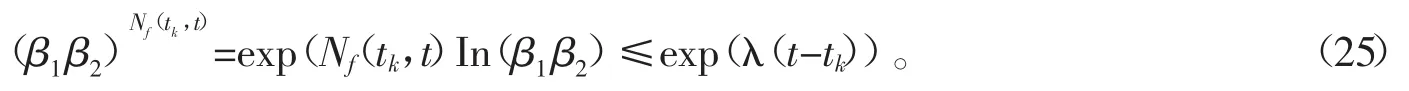
由式(23)~(25),可得
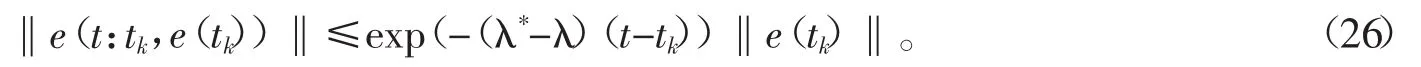
由式(26)可知,当 e(tk)∈Rn/S(r0)时,若切换信号 σ(t)满足定理 2 的条件(a)~(b),那么一定存在 Tk=Tk(e(tk),r0)≥0,使得‖e(tk+Tk)‖=r0成立。显然,{Tk}是一个有界序列,所以有T0=T0(e(t0),r0)≥Tk成立。得证对任意偶数k,如果当t=tk时,状态跟踪误差e(t)的轨迹停留在球域S(r0)外,则在当t>tk时,该轨迹最终必定会回到此球域的边界。
(2)再证明状态跟踪误差e(t)轨迹的有界性。
当 e(tk)∈S(r0)时,由式(14)得
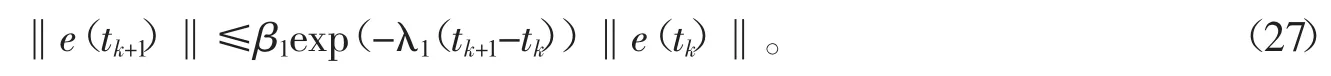
由于式(20)保证了‖e(tk+1)‖≤‖e(tk)‖,因此 e(tk+1)∈S(r0)成立。当 t∈[tk+1,tk+2)时,第 2 个子系统被激活后,则误差切换系统(15)的状态跟踪误差e(t)的轨迹满足
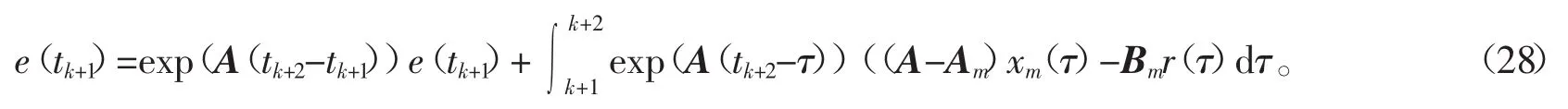
考虑到A,xm(t)和r(t)是有界的,且‖eA‖≤e‖A‖,因此得出下面的不等式

同时,由于 Ts=max{tk+2-tk+1},有
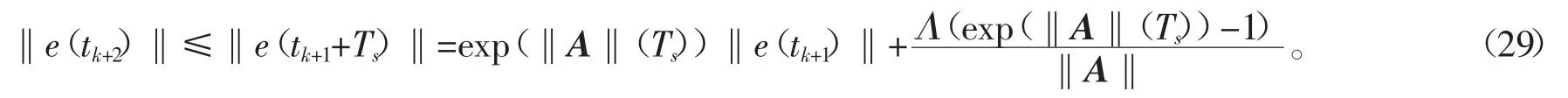
因为式(20)保证了‖e(tk+1)‖≤r0,得到

根据 r*>r0,当 e(tk)∈S(r0)时,有 e(tk+2)∈S(r*)成立。故 e(t)的有界性得证。
(3)当 e(t0)∈Rn/S(r*)时,根据上述(1)和(2)的证明过程,如果切换信号 σ(t)满足定理条件,必然∃T*>0,且T*=T*(e(t0),r*)<T0,使得当t≥t0+T*时,有e(t:t0,e(tk))∈S(r*)成立。显然,当e(t0)∈S(r*)时,上述结果仍然成立,此时T*=0,保证了其全局实用稳定。
证毕。
5 仿真实例
设控制对象状态方程为

该模型的状态为x=(x1(t),x2(t))T,控制器的输入为u=(u1(t),u2(t))T,其中
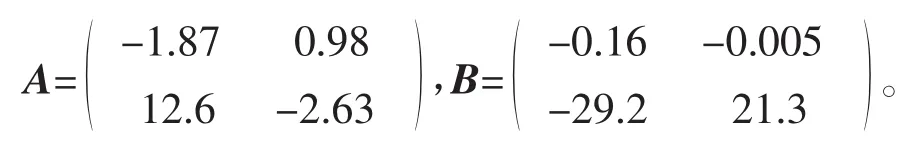
设参考模型状态方程为
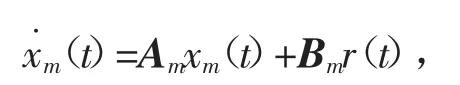
其中

参考模型输入信号为 r(t)=sin(0.1πt)+sin(0.2πt)+sin(πt)。根据式 (9),选择 P1=P2=自适应率增益矩阵为通过计算,令r0=0.5,r*=10。图1给出了满足定理条件的切换信号σ(t)。
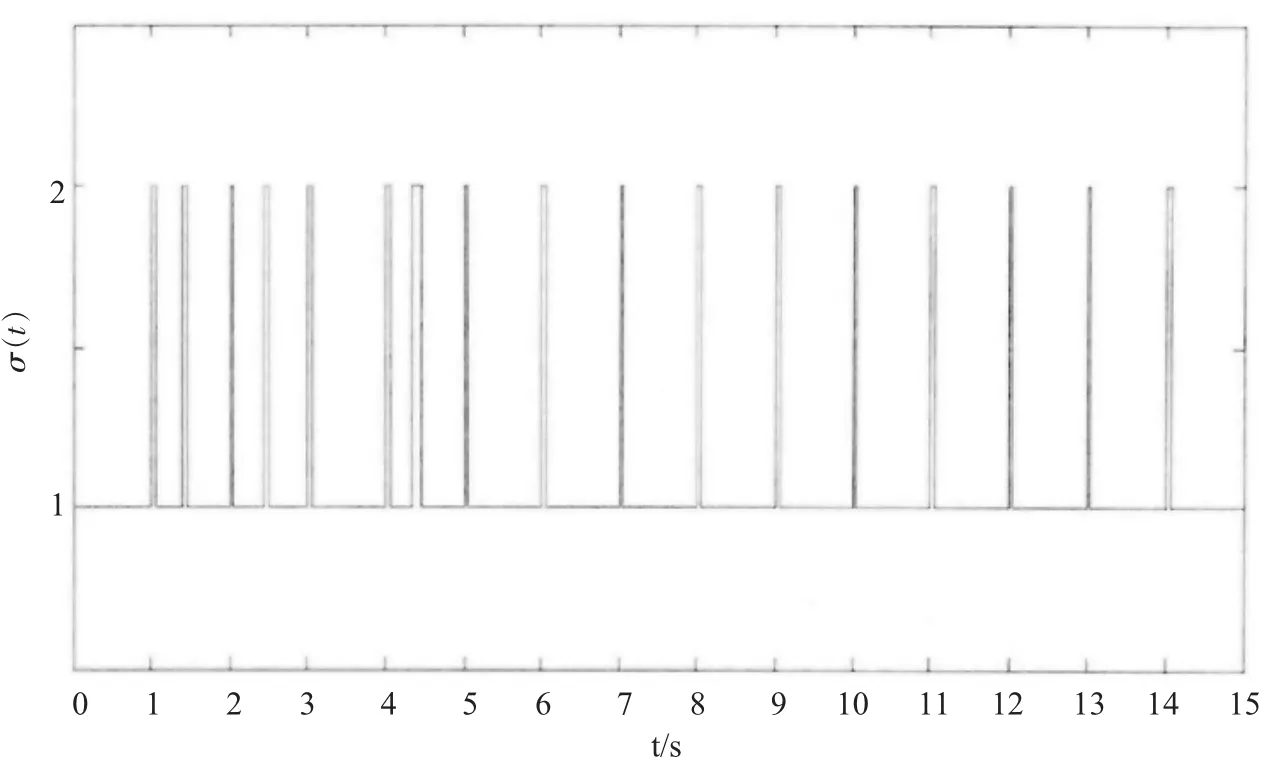
图1 切换信号
设定状态跟踪误差的初始值分别为 e(t0)=(1,1)T及 e(t0)=(12,12)T,即‖e(t0)‖=1.414<r*和‖e(t0)‖=16.97>r*。图2和图3分别描述了上述两种初始值的误差切换系统(15)的状态跟踪误差轨迹。从图2 和图3 可以得出,无论是否满足 e(t0)∈Rn/S(r*),在切换信号 σ(t)的作用下,闭环系统(7)的状态能够跟踪参考模型(2)的状态,并且状态跟踪误差‖e(t)‖的轨迹最终会停留在以r*为半径的球域内,即 e(t:t0,e(t0))∈S(r*)。
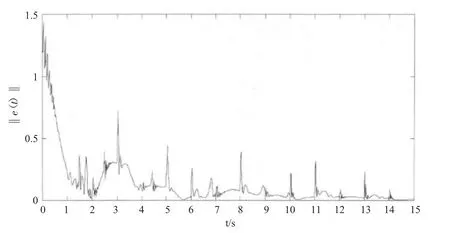
图2 状态跟踪误差(e(t0)=(1,1)T)
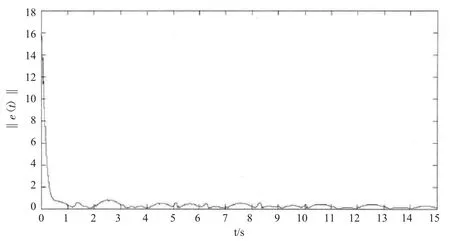
图3 状态跟踪误差(e(t0)=(12,12)T)
6 结语
本文在给定的自适应控制器的条件下,设计其自适应律,解决了一类带有执行器失效的切换系统的模型参考自适应状态跟踪控制的问题。该方法更进一步处理了全部执行器在一个相对较短时间内失效的严重情况。通过用一类具有两个子系统的切换系统来实现带有执行器失效非切换系统的目标控制,并且设计适当的自适应律,让系统可在选定的自适应控制器的作用下实现目标的跟踪控制[11]。

