P2-阶子群X-ss-半置换的有限群

谢凤艳

（安阳学院数理学院，河南安阳455000）

0 引言

本文所考虑的群都是有限群。G表示有限群，|G|表示群G的阶。如果K,H为群G的子群且H正规于K，那么商群K/H称为G的一个截面。G与A4无关表示G的任意一截面不与A4群同构。本文中所有概念和符号都是标准的,未交代的符号和术语参见文献[1-3]。

设H和K是G的子群。如果HK=KH，称H与K是置换的。设X是G的一个非空子集，如果存在一个x∈X,使得HKx=KxH，称H与K是X-置换的[4]。随后,一些广义的X-置换子群，如:X-半置换子群、X-s-半置换子群、X-ss-半置换子群[5]等概念先后被提出。利用某些特定子群的X-置换性，学者们获得了大量成果[4-11]。本文在此基础上,进一步研究p2-阶子群的X-ss-半置换性对有限群结构的影响,得到幂零群的新判断。

1 预备知识

定义1[5]设X是G的一个非空子集，子群H称为在G中X-ss-半置换，如果H在G中有补充子群T,对于T的任意Sylow子群P，只要(p,|H|)=1，就存在x∈X，使得HPx=PxH。

为表示方便,定义1中所有补充子群T的集合记为Xss(H)。

引理1[5]假设X是G的一个非空子集,H≤G,N-⊲G。已知H在G中是X-ss-半置换的。

(1)若X≤D≤G,则H在G中D-ss-半置换；

(2)若H∪X⊆M≤G,则H在M中X-ss-半置换；

(3)若(|H|,|N|)=1或者H为群,其中p为素数,则HN/N在G/N中XN/N-ss-半置换；

(4)若T∈Xss(H)且H≤NG(X),则对任意的g∈G有Tg∈Xss(H)。

引理2设P,Q分别是G的p,q-子群,其中p,q为素数,且PQ≤G。若R是G的次正规子群,则PQ∩R=(P∩R)(Q∩R)。

证 明因为R是G的次正规子群,所以PQ∩R是PQ的次正规子群。又因为P,Q分别是G的p,q-子群且PQ≤G,所以P∩R=P∩PQ∩R,Q∩R=Q∩PQ∩R分别是PQ∩R的Sylow子群和Sylowq-子群。故

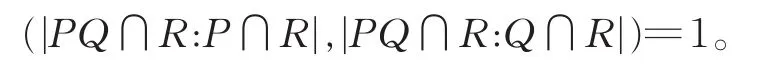
由文献[3]命题1.2.13,得

PQ∩R=(P∩R)(Q∩R)。

引理3[8]设G与A4无关,p是|G|的最小素因子。若G中存在一个正规子群E使得G/E为幂零群且p3|E|，则G为幂零群。

2 主要结论及证明

定理设G与A4无关,X是G的可解正规子群，其中p是|G|的最小素因子。如果G中存在一个正规子群E使得G/E为幂零群且E的每个p2-阶子群在G中X-ss-半置换。那么G为幂零群。

证明假设结论不正确,并令G是一个极小阶反例，分7步进行证明。

（1）Op′(G)=1。

若Op′(G)≠ 1。显然G/Op′(G)与A4无关,XOp′(G)/Op′(G)是G/Op′(G)的可解正规子群。因为G/E为幂零群,所以

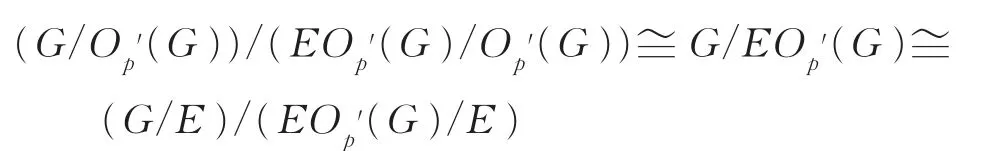
（2）Op(G)≠ 1。

若Op(G)=1。因为Op′(G)=1,所以X=1。设H为E的p2-阶子群。由定理的条件,H在G中X-ss-半置换。设T∈Xss(H)并令K∈Sylq(T),其中q≠p。则G=HT。设Q∈Sylq(G)。由Sylow定理知,G中存在一个元素g使得Q=Kg。因为NG(X)=G,所以H≤NG(X),由引理1得Tg∈Xss(H)。故HQ=QH。即H与G的任意Sylowq-子群是置换的。因为Op′(G)=1且Op(G)=1,所以G的任意极小次正规子群为非循环群。设A是G的任意极小次正规子群,则A不可解。令a∈A。由Sylow定理知Qa∈Sylq(G)。因为H与G的任意Sylowq-子群是置换的,所以HQa=QaH。由引理2,

HQa∩A=(H∩A)(Qa∩A)=(H∩A)(Q∩A)a。因为(H∩A)(Q∩A)a为pq- 群,所以(H∩A)(Q∩A)a可解。从而(H∩A)(Q∩A)a是A的真子群。由文献[12]或文献[1]IV,4.10知,A不是单群。故Op(G)≠1。

（3）设N是G的极小正规子群且N≤Op(G)，则N≤Op(E)

若N不是E的子群。因为N-⊲G且E-⊲G,所以N∩E-⊲G。因为N是G的极小正规子群,所以N∩E=1。显然，(G/N)/(EN/N)≅(G/E)/(EN/E)为幂零群,G/N与A4无关。设M/N是KN/N的p2-阶子群，则

M/N=(M∩EN)/N=(M∩E)N/N≅M∩E。

令H=M∩E,则H为E的p2-阶子群且M=HN。由定理的条件,H在G中X-ss-半置换。由引理1,M/N=HN/N在G/N中XN/N-ss-半置换。由G的极小选择,G/N为幂零群。又G≅G/(N∩E)同构于G/N×G/E的子群且G/E为幂零群,从而G为幂零群。这一矛盾说明N≤E。从而

N≤Op(G)∩E≤Op(E)。

（4）|N|=p，从而N≤Z(G)。

若|N|＞p2。设Gp∈Sylp(G)，令H是包含在N中Gp的正规子群且|H|=p2。断言H-⊲G。由定理的条件，存在T∈Xss(H)。令Q∈Sylq(T)(q≠p），则存在x∈X使得HQx=QxH。由于Qx∈Sylq(G),则HQx为pq-群。从而H∈Sylp(HQx)。由于N是G的极小正规子群且N≤Op(G),那么N为交换群。从而H-⊲N。又因为N-⊲G,所以H是G的次正规子群。故H是HQx的次正规子群。从而H-⊲HQx。即Qx≤NG(H)。又因为H-⊲Gp，所以H-⊲G。而N是G的极小正规子群,与|H|=p2，|N|＞p2矛盾。因此|N|≤p2。若|N|=p2。则|Aut(N)|=p(1)2(p+1)。因为G/CG(N)同构于Aut(N)的一个子群且p是|G|的最小素因子,所以|G/CG(N)||p(p+1)。由文献2引理1.7.11及N的极小正规性得Op(G/CG(N))=1,故|G/CG(N)|≠p。从而(p+1)||G/CG(N)|。因为p是|G|的最小素因子,所以p=2。则G中存在3-阶子群K。因为N是G的极小正规子群且|N|=p2，所以NK≅A4。这与G与A4无关矛盾。故|N|=p。因为p是|G|的最小素因子,所以N≤Z(G)。

（5）Op(E)的阶子群在G中X-ss-半置换。

设H是Op(E)的阶子群。如果H=N,则H在G中X-ss-半置换。如果H≠N,则HN是E的p2-阶子群,故HN在G中X-ss-半置换。

令T∈Xss(HN),则G=(HN)T=H(NT)。设Q∈Sylq(NT),其中q≠p。因为N≤Z(G),所以Q∈Sylq(T)。因为T∈Xss(HN),所以存在x∈X使得(HN)Qx=Qx(HN)。因为HN=(HN)Qx∩Op(E)正规于(HN)Qx且(HN)Qx为pq-群,所以(HN)Qx/(HN)为q-群。从而(HN)Qx/(HN)为幂零群。由引理3可得(HN)Qx为幂零群。即Qx正规于(HN)Qx。从而HQx=QxH。故H在G中X-ss-半置换。

（6）Op(E)≤Z∞(G)。

因为p是|G|的最小素因子,所以只需证明含于Op(E)中的每个G主因子为阶子群。假设L/K是含于Op(E)中G的主因子，使得|L/K|≠p，但对于含于Op(E)中G的主因子U/V，|U|＜|L|且有|U/V|=p。设Gp∈Sylp(G)且A/K是Gp/K的极小正规子群且A≤L。如果A中存在一个阶或者4阶(p=2)元素a,使得A=〈a〉K。令H=〈a〉。则由(5)及定理的条件,H在G中X-ss-半置换。设T∈Xss(H)。令Q∈Sylq(T)(q≠p)，则存在x∈X使得HQx=QxH。由引理2,HQx∩L=(H∩L)(Qx∩L)=H。故H正规于HQx。从而A/K正规于HQxK/K。又因为A/K正规于Gp/K,从而A/K正规于G/K。故L/K=A/K为阶子群,矛盾。所以对A中任意一个阶和4阶(p=2)元素a都有a∈K。因为L/K=(A/K)(G/K)=(AG/K),所以对L中任意一个阶元素或者4阶元素b都有b∈K。设其中U/V是G的主因子。则由文献[13]A(12.3)知,W的Sylowq-子群Q(q≠p)平凡作用于K。由Blackburn定理,Q平凡作用于L/K。从而W/CW(L/K)为群。由文献[2]引理1.7.11知,W≤CG(L/K)。又因为为指数整除1的交换群,所以G/CG(L/K)为指数整除1交换群。由文献[14]I及引理1.3得,L/K为阶群。此矛盾说明(6)成立。

（7）F*(E)=F(E)=Op(E)。

因为Op′(G)=1,所以F(E)=Op(E)。如果F*(E)≠Op(E)。设R/Op(E)为包含在F*(E)中的G-主因子，若R为幂零群，设K为R的正规Hallp′-子群,则K特征于R。因为R-⊲G,所以K-⊲G。因为Op′(G)=1,所以K=1。故R为群。从而R≤Op(E),与R/Op(E)为G-主因子矛盾。故R为非幂零群。又由(6),R/Op(E)为非交换单群。设M是R的极小非幂零群。则M=[A]B,其中exp(A)=p或者4,B为p′-群。若A≤Op(E),则由(6)可得M为幂零群,矛盾。若A不是Op(E)的子群,则存在A中的一个元素a使得a∉Op(E)。令H=〈a〉，若|H|=4,则H在G中X-ss-半置换。由引理1,HOp(E)/Op(E)在G/Op(E)中XOp(E)/Op(E)-ss-半置换。若|H|=p,则|HN|=p2。从而HN在G中X-ss-半置换。因为HOp(E)/Op(E)=HNOp(E)/Op(E),所以由引理1,HOp(E)/Op(E)在G/Op(E)中XOp(E)/Op(E)-ss-半置换。设

T/Op(E)∈(XOp(E)/Op(E))ss(HOp(E)/Op(E)),则G/Op(E)=(HOp(E)/Op(E))(T/Op(E))。

下证HOp(E)/Op(E)在R/Op(E)中s-半置换。显然R/Op(E)=(HOp(E)/Op(E))((R∩T)/Op(E))。对|R/Op(E)|的任意素因子q且q≠p,令M/Op(E)∈Sylq(R/Op(E))。则存在R∩T的Sylowq-子群Q和T的Sylowq-子群Tq使得M=Op(E)且Q≤Tq。因为T/Op(E)∈(XOp(E)Op(E))SS(HOp(E)/Op(E)),所以存在x∈X,使得(HOp(E)/Op(E))(TqOp(E)/Op(E))x为子群。因为X-⊲G且R/Op(E)为G-主因子,所以(R∩X)Op(E)/Op(E)=R/Op(E)或1。若(R∩X)Op(E)/Op(E)=R/Op(E),则R≤X。又因为X是可解群,所以R/Op(E)为可解子群,这与R/Op(E)为非交换单群矛盾。若(R∩X)Op(E)/Op(E)=1,则

[R/Op(E),XOp(E)/Op(E)]=1。

故QxOp(E)/Op(E)=QOp(E)/Op(E)。

从而(R/Op(E))∩(HOp(E)/Op(E))×

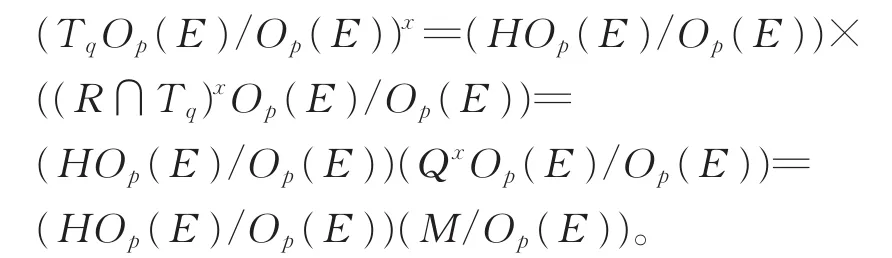
因此,HOp(E)/Op(E)在R/Op(E)中是s-半置换的。由Sylow定理,对R/Op(E)中任意元素α,

(M/Op(E))α∈ Sylq(R/Op(E))。

故(HOp(E)/Op(E))(M/Op(E))α为pq-群子群。

因为R/Op(E)为非交换单群,所以

(HOp(E)/Op(E))(M/Op(E))α

为R/Op(E)的真子群。由文献[12]或文献[1]IV,4.10知,R/Op(E)不是单群。这一矛盾说明(7)成立。

（8）最后的矛盾。

如果E≠Op(E)，设R/Op(E)为包含在E中的G-主因子,仿照(7)的证明过程可得到矛盾。因此E=Op(E)。由G/E为幂零群且E=Op(E)≤Z∞(G)得,G为幂零群。

这一最后的矛盾完成了定理的证明。

推论设G与A4无关,p是|G|的最小素因子。设G中存在一个正规子群E使得G/E为幂零群。如果E的每个p2-阶子群在G中s-半置换，那么G为幂零群。

问题设G与A4无关,X是G的可解正规子群，其中p是|G|的最小素因子。设G中存在正规子群E使得G/E为幂零群，如果E的每个阶子群在G中X-ss-半置换，那么G为幂零群?