一类不定方程的解*
窦晓霞
(宝鸡文理学院数学与信息科学学院,陕西 宝鸡 721013)
整数是数学研究的一个方向。组合数学中就有关于正整数在不同分部量下分拆数的研究[1-2]。对于一个给定的不定方程(或方程组),它是否有解,如果有解,解是不是唯一的,能不能求出它的所有解,这是数论的一个研究方向。有的方程或方程组没有整数解或者没有正整数解[3-6],有的方程或方程组只有有限个整数解[4-5],有的方程或方程组有无数多个整数解[7-8],还有些方程虽然未找到解的具体形式,但却找到了方程是否有解的条件。文献[7-9]给出一类方程有整数解的充分条件;文献[10-11]给出所讨论方程存在无数个解的充要条件;文献[12-13]给出所研究方程的解数上界。另外,有一些方程,大家只关心其特殊解(如文献[14]中方程的素数解等)。除此之外,还可以从其它角度研究不定方程。在已知方程解的基础上,文献[15]就从代数的角度研究了两个二次方程的整数解集。
设a,b,c,d都是正整数,a,b,c是d的因数、互素且不含平方因子。对于方程
ax2+by2+cz2=m+dxyz
(1)
称其满足不等式组
(2)
的整数解为方程(1)的基础解。当m=0时,文献[16]利用二元二次型和同余理论给出了方程
ax2+by2+cz2=dxyz
存在基础解时正整数a,b,c,d的所有可能取值以及对应的基础解,并且指出,方程的其它所有非平凡解(如果方程的解(x,y,z)满足不等式xyz≠0,则称解(x,y,z)是方程的非平凡解)可以由这些基础解求出。当m=1时,利用二元二次型和同余理论,文献[17]解出了方程
ax2+by2+cz2=1+dxyz
存在基础解时正整数a,b,c,d的所有可能取值以及对应的基础解,同时也说明该方程的所有非平凡解可以由这些基础解求出。
利用二元二次型和初等数学的知识,如果不定方程(1)有基础解,本文讨论得到正整数a,b,c,d和非负整数m的所有可能取值以及对应的基础解(x,y,z),进一步得到方程的多个整数解。
在方程(1)中,由于(a,x),(b,y),(c,z)地位对称,所以当三者的顺序互相交换时,得到的依然是同类型的方程。因而对这种由(a,x),(b,y),(c,z)交换顺序引起的新方程及对应的解,看做是相同的,尽可能避免重复讨论。
1 主要结论及证明
定理1设正整数a,b,c互素,不含有平方因子且都是正整数d的因数,m是非负整数。如果(x,y,z)是方程
ax2+by2+cz2=m+dxyz
的基础解,则
(3)
且右边等号当且仅当m=0时成立。
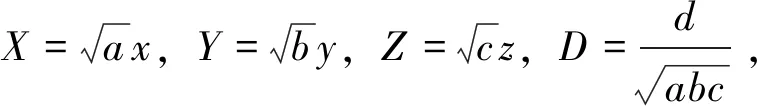
X2+Y2+Z2=m+DXYZ
(4)
在上面的方程中,X,Y,Z地位对称,不妨设1≤X≤min{Y,Z},此时就有2Z≤DXY。
当Y≤Z时,由方程(4)可得
(DXY-2Z)2=(DXY)2-4X2-4Y2+4m
于是
两端平方,整理得
DXY2≤X2+2Y2-m≤3Y2,m=0时右边等号成立。
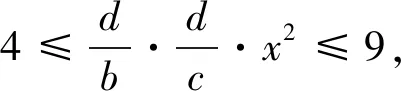
当Z 定理2设正整数a,b,c都不含有平方因子且都是正整数d的因数,(a,b,c)=1,m是非负整数,如果不定方程(1) ax2+by2+cz2=m+dxyz 有基础解,则方程(1)中a,b,c,d,m的可能取值及对应的基础解都出现在表1中。 表1 方程(1)存在基础解的可能情形及对应基础解 证明把方程(1)看成变量y,z的二元二次型 F(y,z)=by2+cz2-(dx)yz(=m-ax2) 这个二元二次函数的判别式Δ(F)=(dx)2-4bc。由于b,c地位对称,可以设b≤c。二元二次型有相关结论[18]:当Δ(F)≤0时,F(y,z)≥0;当Δ(F)>0时,F(y,z)可正可负。在系数a,b,c都不含有平方因子的条件下,结合定理1的结论,当(x,y,z)是方程(1)的基础解时,则x以及系数b,c,d是以下10类可能之一: 接下来,对这些可能逐一进行分析。 于是有0≤m≤a-1。当a=1,m=0时,解得(a,b,c,d)=(1,1,5,5),(x,y,z)=(1,2,1),这是情形5。当a=5,m=0时,解得(a,b,c,d)=(5,1,5,5),(x,y,z)=(1,5,2),这是情形11。当a=5,m=1时,如果z=1,b=1,2,3,不等式组无解。如果z=1,b=4,则b有平方因子,不做讨论。当z=2,b=1时,有(a,b,c,d)=(5,1,5,5),(x,y,z)=(1,4,2),这是情形17。当a=5,m=2时,如果z=1,b=1,不等式组无解。如果z=1,b=3,有(a,b,c,d)=(5,3,15,15),(x,y,z)=(1,2,1),这是情形21。当a=5,m=3时,如果z=1,b=1,不等式组无解。如果z=1,b=2,有(a,b,c,d)=(5,2,10,10),(x,y,z)=(1,2,1),这是情形24。当a=5,m=4时,(a,b,c,d)=(5,1,5,5),(x,y,z)=(1,2,1),这是情形26的特例。 于是有0≤m≤a-2。当a=2,m=0时,解得(a,b,c,d)=(2,1,6,6),(x,y,z)=(1,2,1),这是情形9。当a=3,m=0时,解得(a,b,c,d)=(3,1,6,6),(x,y,z)=(1,3,1),这是情形10。当a=3,m=1时,(a,b,c,d)=(3,1,6,6),(x,y,z)=(1,2,1),这是情形16。当a=6,m=0时,如果z=1,b=1,不等式组无解。如果z=1,b=2,3,6,则c有平方因子,不做讨论。当a=6,m=1,2时,不等式组无解。当a=6,m=3时,有(a,b,c,d)=(6,1,6,6),(x,y,z)=(1,3,1),这是情形25。当a=6,m=4时,(a,b,c,d)=(6,1,6,6),(x,y,z)=(1,2,1),这是情形26的特例。 于是有0≤m≤a-3,所以a=7。当m=0时,不等式组无解。当m=1时,如果z=1,b=1,不等式组无解。如果z=1,b=2,解得(a,b,c,d)=(7,2,14,14),(x,y,z)=(1,2,1),这是情形19。当m=2时,解得(a,b,c,d)=(7,1,7,7),(x,y,z)=(1,3,1),这是情形23。当m=3时,21b2z2+4bm-4ab不是完全平方,不等式组无解。当m=4时,(a,b,c,d)=(7,1,7,7),(x,y,z)=(1,2,1) ,这是情形26的特例。 于是当a=m=1时,解得(a,b,c,d)=(1,b,b,2b),(x,y,z)=(1,z,z),这时,bz2≥1。这是情形13。当a=m=2时,解得(a,b,c,d)=(2,b,b,2b),(x,y,z)=(1,z,z),这时,bz2≥2,且(2,b)=1。这是情形20。 于是有0≤m≤a-1。当a=1,m=0时,解得(a,b,c,d)=(1,2,3,6),(x,y,z)=(1,1,1),这是情形6。当a=2,m=0时,如果z=1,t=1,不等式组无解。因为a,b,c不含平方因子,所以z=1,t=2不做讨论。当a=2,m=1时,解得(a,b,c,d)=(2,2,3,6),(x,y,z)=(1,1,1),这是情形15。当a=3,m=0时,如果z=1,t=1,不等式组无解。因为a,b,c无平方因子,所以z=1,t=3不做讨论。当a=3,m=1时,如果z=1,t=1,不等式组无解。因为a,b,c无平方因子,所以z=1,t=2不做讨论。当a=3,m=2时,(a,b,c,d)=(3,2,3,6),(x,y,z)=(1,1,1),这是情形20的特例。当a=6,m=0时,如果z=1,t=1,不等式组无解。如果z=2,t=1,有(a,b,c,d)=(6,2,3,6),(x,y,z)=(1,3,2),这是情形12。当a=6,m=1时,如果z=1,t=1,不等式组无解。如果z=1,t=5,有(a,b,c,d)=(6,10,15,30),(x,y,z)=(1,1,1),这是情形18。如果z=2,t=1,3t2z2+2tm-2at不是完全平方,不等式组无解。当a=6,m=2时,如果z=1,t=1,不等式组无解。如果z=2,t=1,有(a,b,c,d)=(6,2,3,6),(x,y,z)=(1,2,2),这是情形22。当a=6,m=3,4,5时,不等式组都没有解。 于是有0≤m≤a-1。当a=1,m=0时,解得(a,b,c,d)=(1,1,2,4),(x,y,z)=(1,1,1),这是情形4。当a=2,m=0时,解得(a,b,c,d)=(2,1,2,4),(x,y,z)=(1,2,1),这是情形8。当a=2,m=1时,解得(a,b,c,d)=(2,1,2,4),(x,y,z)=(1,1,1) ,这是情形13的特例。 当a=1时,则z=1,b=1,解得(a,b,c,d)=(1,1,1,3),(x,y,z)=(1,1,1),这是情形2。当a=3时,如果z=1,b=1,不等式组无解。如果z=2,b=1,5b2z2-4ab不是完全平方。因为(a,b,c)=1,所以c=b=3不做讨论。 所以(a,b,c,d)=(1,b,b,b),(x,y,z)=(2,z,z),这里bz2≥4。这是情形26。 于是有0≤m≤4a-1。当a=1,m=0时,如果z=1,b=1,不等式组无解。如果z=2,b=1,解得(a,b,c,d)=(1,1,2,2),(x,y,z)=(2,2,2),这是情形3。当a=1,m=1时,如果z=1,b=1,不等式组无解。如果z=1,b=3,解得(a,b,c,d)=(1,3,6,6),(x,y,z)=(2,1,1),这是情形16。当a=1,m=2时,如果z=1,b=1,解得(a,b,c,d)=(1,1,2,2),(x,y,z)=(2,2,1) ,这是情形20的特例。因为a,b,c没有平方因子,所以z=1,b=2不做讨论。当a=1,m=3时,不等式组无解。当a=2,m=0时,如果z=1,b=1,不等式组无解。如果z=2,b=1,解得(a,b,c,d)=(2,1,2,2),(x,y,z)=(2,4,2),这是情形7。当a=2,m=1时,如果z=1,b=1,不等式组无解。如果z=2,b=1,解得(a,b,c,d)=(2,1,2,2),(x,y,z)=(2,3,2),这是情形14。如果z=1,b=7,解得(a,b,c,d)=(2,7,14,14),(x,y,z)=(2,1,1),这是情形19。当a=2,m=2时,如果z=1,b=1,不等式组无解。如果z=2,b=1,2b2z2+bm-4ab不是完全平方,不等式组无解。如果z=1,b=3,解得(a,b,c,d)=(2,3,6,6),(x,y,z)=(2,2,1) ,这是情形22。当a=2,m=3时,如果z=1,b=1,不等式组无解。如果z=2,b=1,2b2z2+bm-4ab不是完全平方,不等式组无解。如果z=1,b=5,解得(a,b,c,d)=(2,5,10,10),(x,y,z)=(2,1,1),这是情形24。当a=2,m=4时,如果z=1,b=1,不等式组无解。如果z=2,b=1,解得(a,b,c,d)=(2,1,2,2),(x,y,z)=(2,2,2),这是情形26的特例。当a=2,m=5,6,7时,不等式组无解。 当b=1时,如果z=1,2,不等式组无解。如果z=3,解得(a,b,c,d)=(1,1,1,1),(x,y,z)=(3,3,3),这是情形1。如果z=4,5b2z2-36b不是完全平方,不等式组无解。当b=3时,如果z=1,不等式组无解。如果z=2, 2b2z2+bm-4ab不是完全平方,不等式组无解。因为a,b,c没有平方因子,所以b=9不做讨论。 证毕。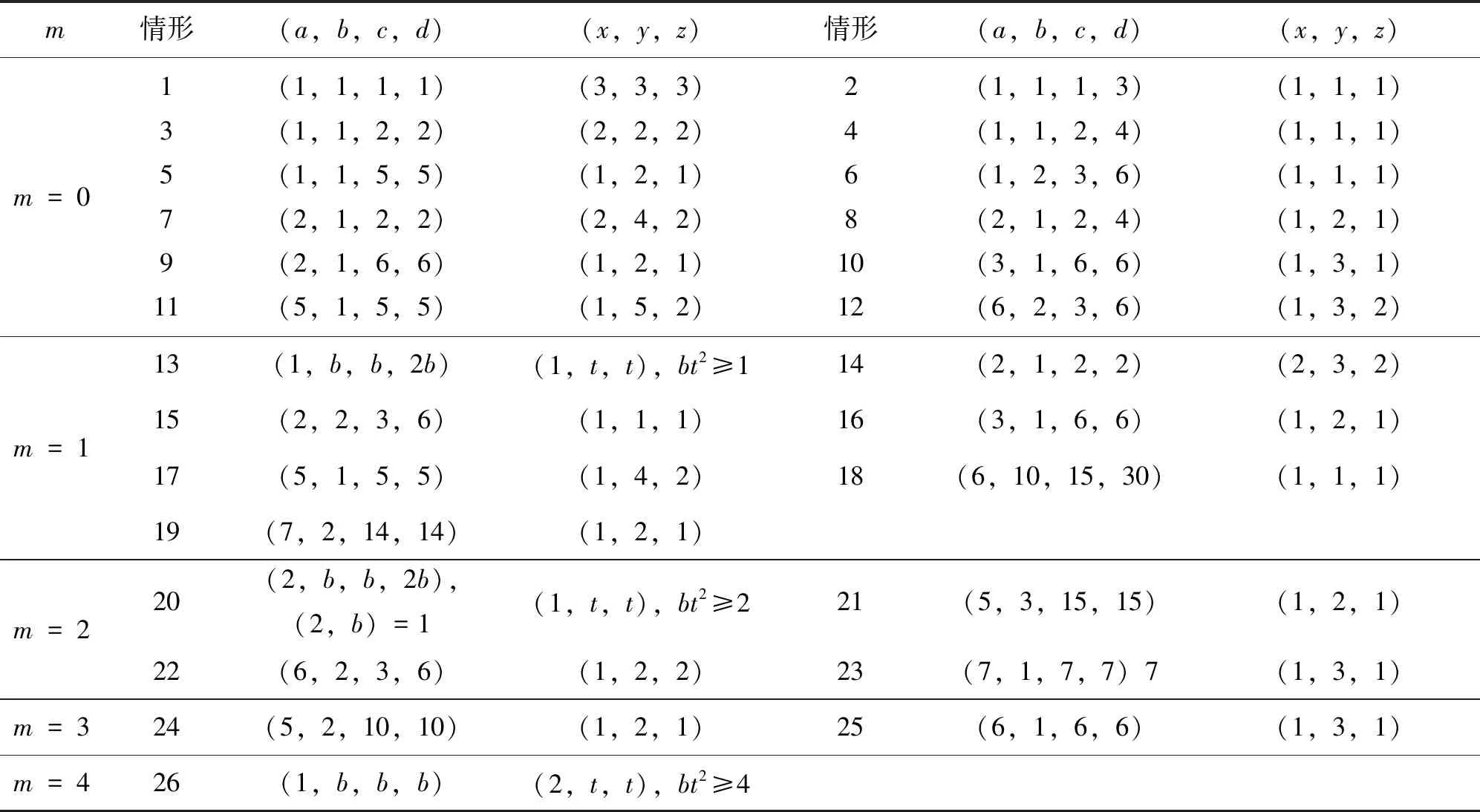
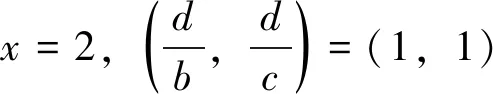
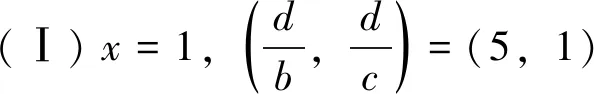
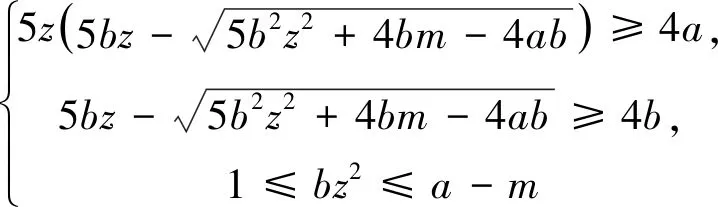
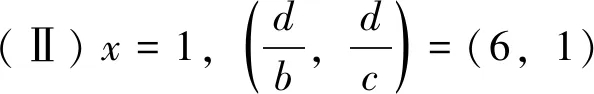
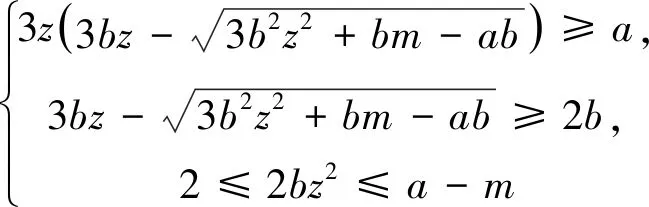
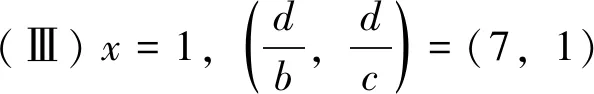
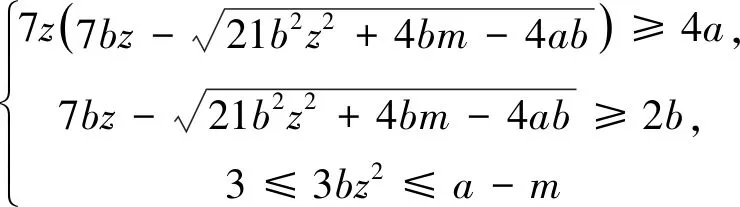
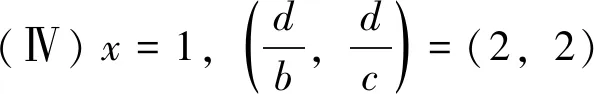
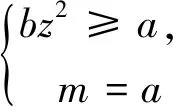
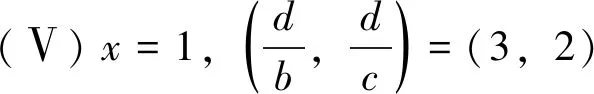
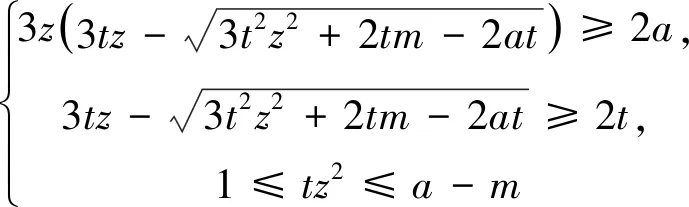
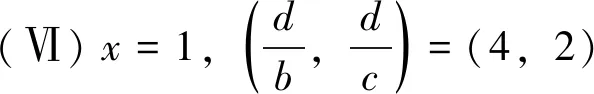
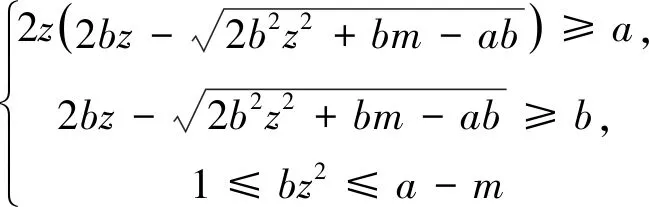
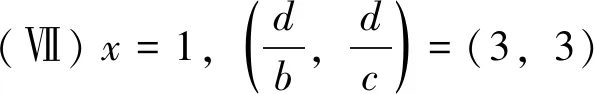
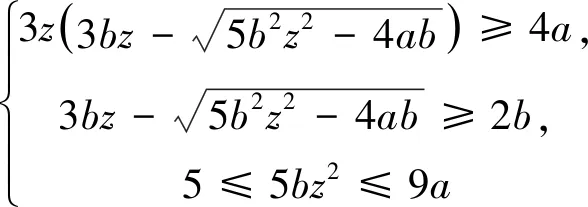
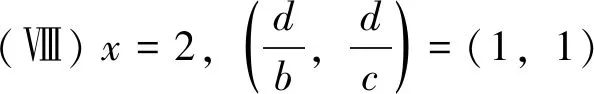
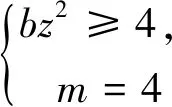
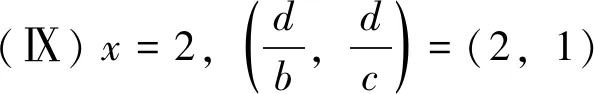
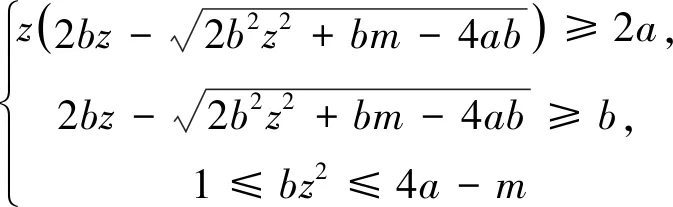
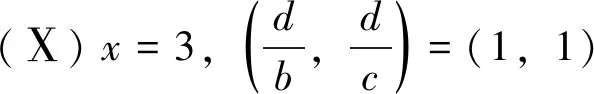
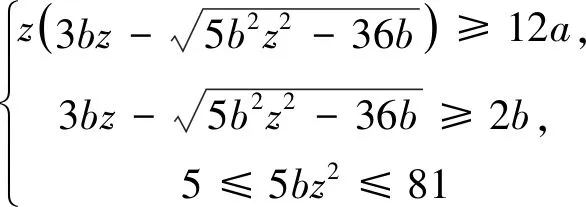
2 总 结