再谈数字信号处理课程中几种变换的关系

刘会衡，张军

（湖北文理学院 物理与电子工程学院，湖北 襄阳 441053）

数字信号处理课程是电子信息类和电气类专业本科生继信号与系统课程之后，必须学习的一门专业基础课程．信号与系统课程主要讲解模拟信号的基本概念、模拟系统的时域和变换域分析方法[1-4]．数字信号处理课程主要讲解数字信号的基本概念、数字系统的时域和变换域分析方法，以及滤波器的设计方法[5-7]．本课程中涉及几种重要的变换，包括连续或离散信号的傅里叶变换（FT）、连续信号的拉普拉斯变换（LT）、离散信号的 Z变换（ZT）、连续周期信号的傅里叶级数（FS）、离散周期信号的傅里叶级数（DFS），以及离散信号的离散傅里叶变换（DFT）[8-9]．学生在学习的过程中，往往对这几种变换及其关系混淆不清，导致学习和理解起来非常困难，这也是本课程教学的难点[10]．本文对数字信号处理课程中的这几种重要变换进行了深入的分析，理清其中的关系，分析各种变换的本质，使复杂的变换理解起来更加通俗易懂．

1 4种傅里叶变换

信号从时域是否连续、是否周期，将信号分成四大类：连续非周期信号、连续周期信号、离散非周期信号和离散周期信号．本科生分别在信号与系统和数字信号处理课程中学习这些内容（部分内容在有些教材中也有交叉）．对系统进行分析，可以在时域进行，也可以在变换域进行．对于连续系统，时域分析主要是求解微分方程，变换域分析主要是频域分析法和S域分析法．对于离散系统，时域分析主要是求解差分方程，变换域分析主要是频域分析法和Z域分析法．无论是连续信号还是离散信号，最重要的变换就是傅里叶变换，具体见表1．信号在时域和频域的周期性和连续性是交叉一一对应的．一个域的周期一定会造成另一个域的离散，一个域的非周期一定会造成另一个域的连续；一个域的连续一定会造成另一个域的非周期，一个域的离散一定会造成另一个域的周期．

表1 4种傅里叶变换

1.1 连续非周期信号的傅里叶变换（FT）

连续非周期信号x（t）若满足绝对可积条件

则存在傅立叶变换X(jΩ)，其傅里叶变换

其中：Ω为模拟角频率，单位rad/s．

以单个方波脉冲为例，假设脉宽τ=2，即

则其对应的傅里叶变换为

方波脉冲的波形和频谱见图1．从图1中可以看出，X(jΩ)为连续非周期的频谱．

图1 矩形脉冲及其频谱

1.2 连续周期信号的傅里叶级数（FS）

连续周期信号不满足绝对可积的条件，所以它不存在傅里叶变换，但可以展开成傅里叶级数．以指数函数形式的傅里叶级数为例，周期函数～x(t)的傅里叶级数变换对为

以周期矩形脉冲为例，假设周期T=8，脉冲宽度为τ=2

则其对应的傅里叶级数为

周期矩形脉冲的波形和FS系数见图2．从图2中可以看出，X(jkΩ)为非周期的离散谱．

图2 周期矩形脉冲及其傅里叶级数

1.3 离散非周期信号的傅里叶变换（FT）

离散非周期信号x(n)，若满足绝对可和条件

则存在傅里叶变换，其傅里叶变换对为

其中：ω为数字频率，单位rad．

以矩形序列RN(n)为例，假设N=4，即

其傅里叶变换为

矩形序列的序列图和频谱见图3．从图3中可以看出，序列的傅里叶变换是周期的，周期是2π．由于X(ejω)的周期性，实际分析过程中，只关注一个周期[02π]或[-π π]内的信号频谱．由于信号频谱一般都是关于ω=0对称的，所以分析信号往往只需要观察[0 π]范围内的频谱特征．

1.4 离散周期信号的离散傅里叶级数（DFS）

离散周期信号不满足绝对可和的条件，所以它不存在傅里叶变换，但可以展开成傅里叶级数．从计算机处理信号的角度来看，计算机只能处理数字信号，因此要求信号在时域和频域都是离散的．但是前面3种变换至少在一个域是连续的，不适合计算机处理，而DFS变换在时域和频域都是离散的，因此是最适合计算机处理的一种变换方式．周期序列的DFS变换对为

图3 矩形序列及其频谱

以周期矩形序列为例

其中：x(n)=R4(n)；周期N=8；m为正数．周期矩形序列的序列图和DFS系数见图4．从图4中可以看出，周期序列的频谱是离散的、周期的．

图4 周期序列及其离散傅里叶级数

2 各种变换之间的关系

信号从时间上是否连续可以分为两大类：连续时间信号和离散时间信号，各种变换及其关系见图5．

图5 信号的各种变换及其关系

2.1 连续信号的FT与LT

对于连续时间信号x（t），如果x（t）满足绝对可积的条件，则存在傅里叶变换，也就是非周期信号的FT．但是有些信号即使是非周期的，也可能不满足绝对可积的条件，此时就无法用傅里叶变换来分析．但是如果给此信号乘以一个指数形式的衰减因子e-σt（σ为实常数），在σ满足一定的条件下，x(t)e-σt能够满足绝对可积的条件

此时x(t)e-σt的傅里叶变换为

令复变量s=σ+jω，则可得到Laplace正变换

从分析可知，σ需要满足一定的条件x(t)e-σt才绝对可积，σ满足的这一条件即Laplace变换的收敛域．对于 Laplace变换，当σ=0时，s=jω，Laplace变换就成了傅里叶变换，即虚轴上的拉普拉斯变换为傅里叶变换．反之，若σ无法取到 0值，则傅里叶的信号变换不存在．由此可见，Laplace变换是傅里叶变换的推广，但并不是所有函数的Laplace变换都存在，必须满足收敛域的要求．

2.2 连续信号的FT与FS

对于连续周期信号，可展开成傅里叶级数，但是不存在傅里叶变换．为了将周期信号和非周期信号的研究统一起来，引入了奇异函数δ(Ω)，从而使周期信号也可以利用傅里叶变换进行分析，即广义傅里叶变换．由FS知

为了表述方便，这里将基波角频率表示为Ω0．对式（17）取傅里叶变换

因此，利用奇异函数δ(Ω)，周期函数也可进行傅里叶变换，其频谱同傅里叶级数系数一致，只是用冲激函数表示频谱分量而已．

另一方面，从周期函数的频谱或者傅里叶级数系数可以看出，周期函数频谱可以看作是对非周期信号频谱的频域抽样，抽样间隔为基波角频率频域抽样将造成信号在时域周期延拓，延拓周期为T，故而非周期信号就变成了周期信号，这就是周期信号FS和非周期信号FT的关系．

2.3 离散信号的FT与ZT

Z变换的定义为

其存在的条件是幂级数收敛，即

满足此条件z的取值范围称为Z变换的收敛域．z为复平面变量，若将其表示为模和幅角的形式

代入式（19），得到

显然，如果r=1，则Z变换就等于傅里叶变换，即

r=|z|=1，在z平面上即单位圆．因此，单位圆上的Z变换即傅里叶变换．如果ZT的收敛域不包含单位圆，则FT不存在．由此可见，Z变换是傅里叶变换的推广，但并不是所有函数的Z变换都存在，必须满足收敛域的要求．

2.4 离散信号的FT与DFS

对于离散周期信号，可展开成傅里叶级数，但是傅里叶变换不存在．如果引入了奇异函数δ(ω)，则可将周期序列和非周期序列分析统一起来．由DFS可知

对式（24）取傅里叶变换

另一方面，从周期序列的频谱或者傅里叶级数系数可以看出，周期序列频谱可以看作是非周期序列的连续频谱在频域抽样，每个周期（2π）内抽样N个点，抽样间隔，也即基波角频率．频域抽样将造成信号在时域周期延拓，延拓周期为N，则非周期序列就变成了周期序列，这就是周期序列的DFS和非周期序列FT的关系．

3 连续信号的FT和离散信号的FT

要建立连续信号和离散信号傅里叶变换之间的关系，就需要从模拟信号的数字化过程来分析．模拟信号转换为数字信号的第一步就是抽样，假设每隔T秒抽样一次，有

当t=nT时，连续变量t就变成了离散变量n，微分就变成了求和．抽样信号x(nT)简记为x(n)，并考虑到数字频率ω与模拟角频率Ω的关系ω=ΩT，可得到

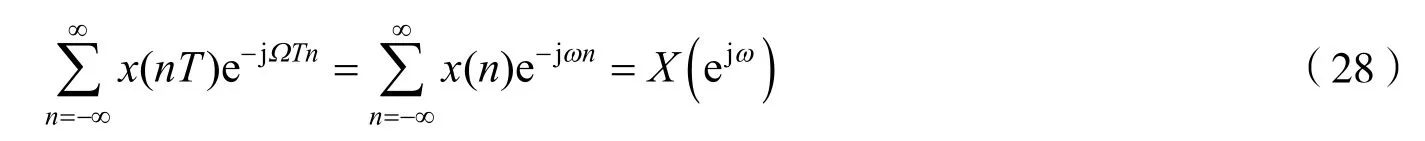
式（28）即离散信号的傅里叶变换DFT．

时域抽样会造成频域周期延拓．从时域抽样定理知道，频域延拓周期为抽样角频率Ωs．因此，从连续信号的角度来看，离散信号的傅里叶变换是周期的，周期是Ωs．而从离散信号的角度来看，其频谱周期是2π，其实二者并不矛盾．当模拟角频率为Ωs时，数字频率为

因此，从不同角度来看离散信号的周期都是一致的．

4 DFT与DFS，ZT，FT的关系

4.1 DFT与DFS

DFS并不适合计算机处理，虽然DFS在时域和频域都是离散的，但都是周期的，计算机无法处理无穷尽的信号．从周期序列的基本性质知道，每个周期的信号都是重复的，因而可以只分析某个周期的信号和频谱，这就是有限长序列的傅里叶变换，即离散傅里叶变换DFT．有限长序列在时域可以看作周期序列在主值区间上的主值序列；类似地，其频谱也可以看作离散傅里叶级数系数在主值区间上的主值序列．从而可以得到DFT变换对

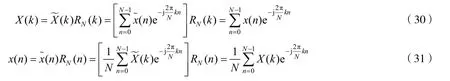
其中：N为序列的长度，也是DFS的周期．从式（30）可以明显看出，DFT变换就是DFS的主值序列．

这就是DFT和DFS的关系．

4.2 DFT与ZT

从式（19）和式（30）对比可以得到DFT与ZT的关系

4.3 DFT与FT

从式（9）和式（30）对比可以得到DFT与FT的关系

以有限长序列x(n)=R4(n)为例，其8点的DFT为

16点的DFT为

它们对应的DFT幅频特性见图6，其中虚线为x(n)的FT变换．从图6中可以明显看出，DFT变换就是对FT变换在[02π]上等间隔采样，将连续频谱转换为了离散频谱．

图6 x（n）的DFT和FT的关系

5 结语

从信号的连续与离散、周期与非周期，可以将傅里叶变换分为4类，即连续非周期信号的FT，离散非周期信号的FT，连续周期信号的FS和离散周期信号的DFS．将连续非周期信号的FT推广就得到拉普拉斯变换，而虚轴上的LT即FT．将离散信号的FT推广就得到了Z变换，而单位圆上的ZT即FT．连续信号x(t)抽样后就成了离散信号x(n)，对二者分别作傅里叶变换就得到了二者的傅里叶变换（FT）X(jΩ)和X（ejω），时域抽样造成频域周期延拓，所以X（ejω）是X(jΩ)以2π为周期的周期延拓信号．离散信号的DFT变换可看作是周期序列傅里叶级数主值区间上的系数值，而离散序列则可看作是周期序列的主值序列．另一方面，DFT变换是Z变换在单位圆上的N点等间隔抽样，也是FT变换在区间[02π]内的N点等间隔抽样．通过理清各种变换之间的关系，学生可以更好地学习和理解数字信号处理课程中几种重要的变换，从而更好地掌握数字信号处理的基本理论和基本方法．