一种求解旅行商问题的演化算法研究
许 冲,钟 玮,刘欣欣
(闽南师范大学计算机学院,福建漳州363000)
1948 年由美国兰德公司推动的TSP(Traveling Salesman Problem)是一个较古老的巡回旅行商问题[1],成为近代组合优化领域的一个典型难题,已被证明为NP 难题.TSP 描述为在一个加权无向图中,寻找一个边的权值之和最小的Hamilton圈.
随着TSP的研究和利用的不断扩展,图的复杂程度不断加大,导致TSP求解的搜索空间不断加大.诸多学者也提出了多种不同的求解TSP 问题的算法.其中,湖水能量算法[2]就是一种高效的求解算法,但其缺点在于找到最优解的概率较低.郭涛算法[3](GT)是一种改进遗传演化算法,被证明是一种效率很高的算法.但是,随着图的规模和复杂度增大,GT算法找到最优解的概率不断下降.蔡之华[4],谢大同[5]等给出了一种对郭涛算法或其Inver-over算子[3]进行改进的求解TSP问题的演化算法,经过实验证明其找到最优解的能力虽有改善,但仍不够理想,其在实例CHN144上找到最优解的概率仅为0.7.本文采用粒子群[6]的基因片段插入[7-8]与Inver-over算子结合,随机的在粒子中插入其他粒子的片段,以达到扩大粒子搜索范围的作用,从而防止算法解的早熟.
1 新的演化算法
为方便算法描述,先对算法中使用的参数、符号和数据作以下说明.
给定n 个城市{1,2,…,n}以及对应的坐标值,记两个城市i 和j 之间的距离d(i,j).用c1c2…cn来表示TSP的一个解的路径(其中1 ≤ci≤n,且c1c2…cn互不相同),并称c1c2…cn为一个个体p,一组个体的集合称为P ,第i 个个体称为Pi. c1c2…cn个体的长度定义为d(c1,c2)+ d(c2,c3)+ …+ d(cn-1,cn)+ d(cn,c1). 设1 ≤t ≤n - 1,长度为l 的路径cici+1…ci+t称为个体c1c2…cn的一个起始位置为i,长度为t 的基因片段(若下标大于n,则将此下标除n取余数).
1.1 郭涛算法
郭涛算法提出的Inver-over算子具有杂交和变异的演化特征,算法在设置群体规模参数后,按照随机倒置概率ρ 对个体进行盲目或自适应的两种方式倒置,直到满足结束条件,算法结束.其中,倒置操作作用于个体的局部,随机倒置概率ρ 一般设置很小,大部分倒置操作来自群体中的其他个体,达到加快收敛的目的;极少部分随机产生,其作用打破收敛趋势,增加搜索全局最优解的可能性.郭涛算法对个体Pi操作如图1所示.
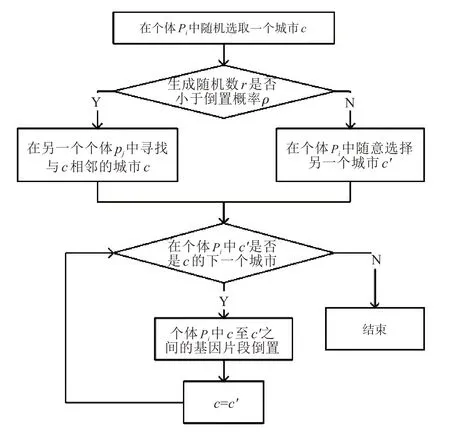
图1 郭涛算法的Inver-over算子Fig.1 Inver-over operator of Guo Tao algorithm
TSP 结果得到的路径是个闭合的环路,每次操作都对基因片段进行反转,算法运行的速度快.因此,郭涛算法相比于其他演化算法在求解质量和速度上都有较好效果,这主要在于算法中群体趋优信息得到了充分的利用.但是在试验中也发现,郭涛算法对于小规模TSP问题的求解效果优异,但是对于解决规模较大的TSP 问题,其寻找全局最优解的效果就大为下降.这主要是由于该算法的操作迭代在前期的收敛速度很快,而到了后期,群体中的粒子所表示的解的路径都是没有交叉的较优环形路径,所以算法在后期的收敛速度明显变慢,且容易陷入局部最优解.
1.2 基因片段插入运算
基因片段插入对个体Pi的运算如图2所示.
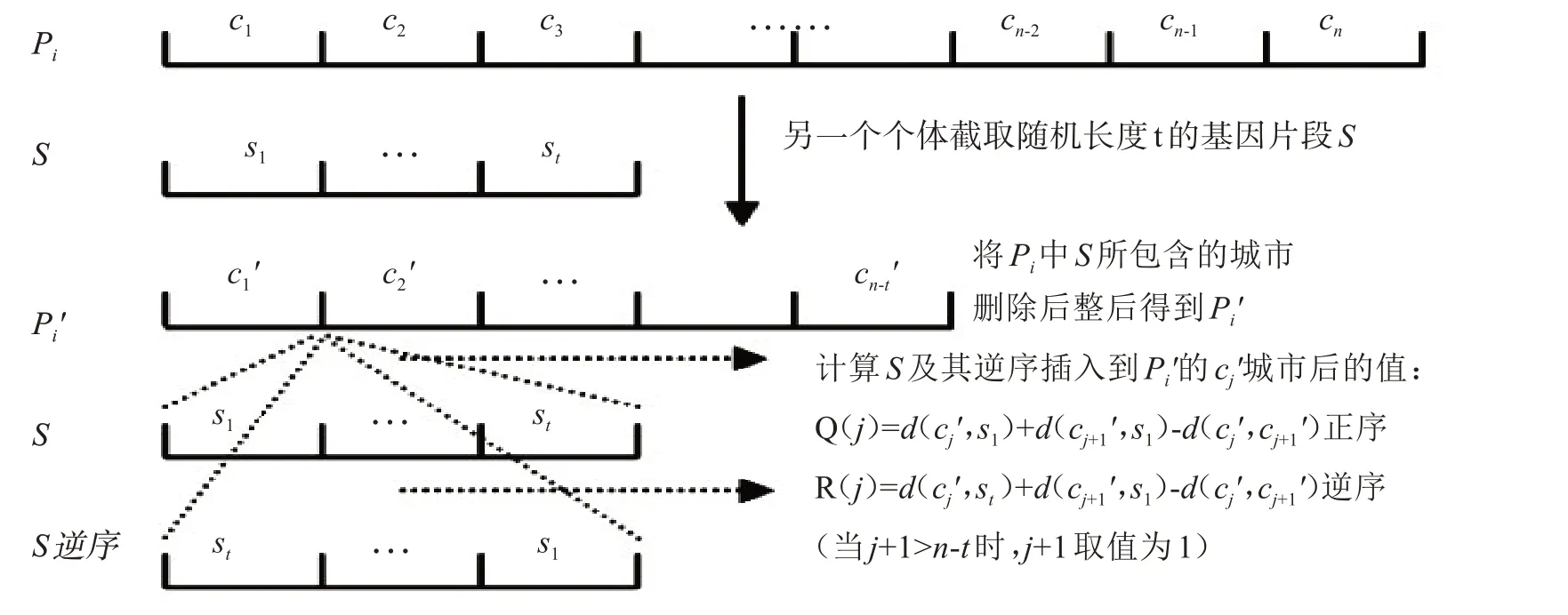
图2 基因片段插入运算Fig.2 Gene fragment insertion
取Q( j),R( j)中的最小值,若最小值为Q(m),则将基因片段S 正序插入到P'i的cm与cm+1之间,若最小值为R(m),则将基因片段S逆序插入到P'i的cm与cm+1之间,得到新的个体.
基因片段插入运算的主要思想是在于通过从群体的其它个体中截取部分基因片段插入到原个体,以达到保持个体的多样性和改善个体局部的目的.
1.3 混合算法
根据算法分析和试验结果,本文将郭涛算法的Inver-over算子与基因片段插入算法相融合,提出了一个新的算法.混合算法描述如下.
Input:城市数n及各城市对应位置坐标.
Output:输出全局最优解global_best及其路径长度gb_length.
Step1:设置种群中个体个数N_ALL(一般设置为N_ALL = 4n)及算法迭代次数T.
初始化所有个体,其中n个个体利用贪心算法从城市i开始产生{P1,P2,…,Pn-1,Pn},其余N_ALL_n个个体采用随机方式产生,得到N_ALL 个个体的种群{P1,P2,…,Pn,Pn+1,…,PN_ALL},记迭代计数变量T_number = 0.
Step 2:将个体Pi的值保存到R,即(R = Pi).
1)使用郭涛算法对个体R进行操作.
2)生成3个随机数j(1 ≤j ≤N_ALL,j ≠i)、s(1 ≤wz ≤n)、k(2 ≤k ≤n/6),其中k = 2 +(int)((rand()%(n/6 -1))*(1 - T_number%(2*n)*0.98/(2*n))).然后,从个体Pj的起始位置为s,长为k 的基因片段gene,并把gene采用基因片段插入算法插入到个体R中.若R的路径长度小于Pi路径长度,则Pi= R.
Step 3:T_number = T_number + 1.
Step 4:如果T_number <T,则执行Step 2;否则转至Step 5.
Step 5:从种群中找出最优个体,并将个体及其路径长度分别保存至global_best和gb_length.
此算法不仅保持种群中个体的多样性,扩大种群对解的搜索能力,同时对个体的局部进行有针对性的改良.算法中,空间复杂度主要体现在种群的存储空间,为O(n2).郭涛算法的时间复杂度为O(n2),基因片段插入的时间复杂度为O(n3),迭代次数为T,因此算法的时间复杂度为O(n3T).
2 仿真试验
仿真试验采用TSPLIB 中的Eil51、st70、ch150、pr226 以及中国144 个城市的Ch144 等5 个实例作为试验用例.在试验过程中,将5 组用例分别采用郭涛算法、基因片段插入算法和混合算法各重复运行50 次,以最多迭代n2次为限制,得到对比数据如表1所示.
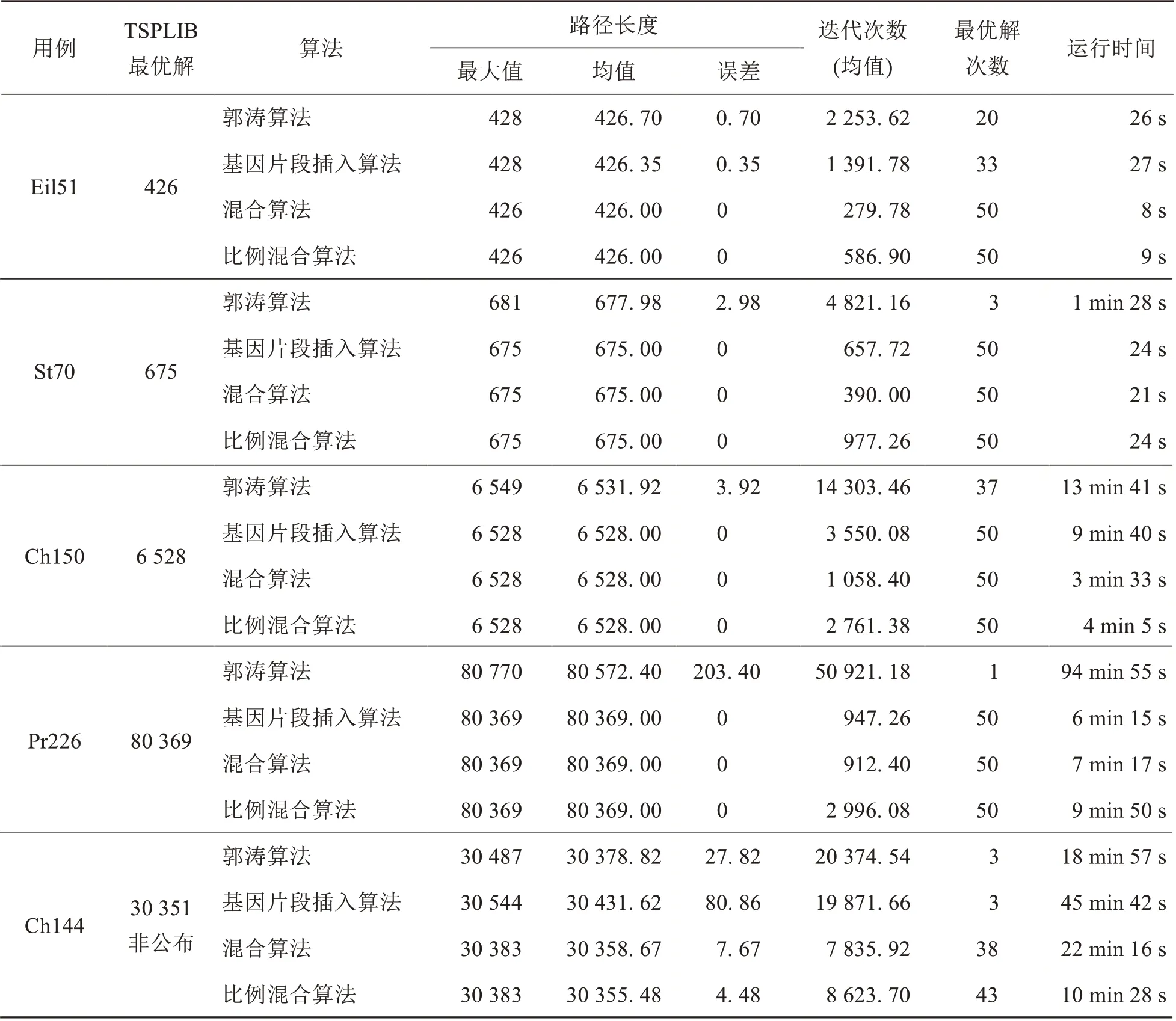
表1 测试结果对比Tab.1 Comparison of test results
从表1中的试验对比数据可见,使用郭涛算法单独求解时,当图的规模变大后,其迭代次数极具增加,且找到最优解的概率也不断下降.而单独使用基因片段插入算法进行求解时,效率较不稳定,且找到最优解的概率也不够理想.但采用两个算法结合的混合算法,对上述5 个试验用例进行50 次试验均找到最优解.虽然该混合算法的时间复杂度较高,但其优异的搜索能力和收敛速度,其找到最优解的迭代次数远低于n2,也低于其它两个算法的迭代次数,即使在图的规模增大的情况下,其迭代次数也未明显增加.
3 结论
本文将两种算法融合产生一种新的求解旅行商问题的演化算法.试验结果表明,该算法不仅能够有效地提高找到最优解的概率,而且运行效率很高,是一种有效可行的算法.

