注重直观想象引领深化溯源解法探究落实数学运算素养

◇ 江西 章建荣 刘 臻

史宁中教授曾经说过：“数学教育的最终目标是让学习者会用数学眼光观察现实世界、会用数学的思维思考现实世界、会用数学的语言表达现实世界.”用简洁的三句话深刻阐述了数学抽象、直观想象、逻辑推理、数学运算、数学建模、数据分析六大素养.史宁中教授还提出数学基本思想归结于三大类：抽象思想、推理思想与模型思想.

《普通高中数学课程标准(2017年版)》明确指出着力发展核心素养，其中数学运算就是六大核心素养之一.数学运算素养是指在明晰运算对象的基础上，依据算法法则准确地解决数学问题的素养.从运算求解能力到数学运算素养是对数学运算的进一步完善与升华.

考试大纲对数学运算能力进行了明确的阐述，运算能力是思维能力和运算技能的结合.运算包括对数字的计算、估值和近似计算，对式子的组合变形与分解变形，对几何图形各几何量的计算求解等.运算能力包括分析运算条件、探究运算方向、选择运算公式、确定运算程序等一系列过程中的思维能力，也包括在实施运算过程中遇到障碍再调整运算的能力.

解析几何的考查中，要求学生建立标准方程，运用代数方法进一步认识圆锥曲线的性质以及直线与圆锥曲线的位置关系；借助几何图形的特点，形成解决问题的思路，通过直观想象和代数运算得到结果，并给出几何解释，解决问题.考查内容聚焦学生对重要数学概念、定理、方法、思想的理解和应用，强调基础性、综合性，注重数学本质、通性通法，淡化解题技巧，融入数学文化.

解析几何是数学的重要分支，解析几何问题常常涉及多个知识点，对学生能力要求较高，很多学生在考试中得分不理想.笔者结合一道典型例题的根源与解法探究，谈谈如何引导学生理解运算对象、掌握运算法则、探究运算思路、选择运算方法、设计运算程序、求得运算结果，着力培养学生的数学运算素养.

1 问题呈现

题目已知椭圆的右焦点为F，焦距为4，过点F 的直线l与椭圆E 相交于A，B 两点，点A 关于原点O 的对称点为C，当l 的斜率存在时，直线AB 和BC 的斜率之积为.

(1)求椭圆E 的方程；

(2)求△OBC 的面积的最大值.

命题意图本题主要考查椭圆的“第三定义”、椭圆的对称性、直线与椭圆的位置关系、焦点弦、二次方程的根与系数的关系，考查数形结合思想、化归与转化思想，考查逻辑推理和数学运算等核心素养.

2 回归教材

教材是高考试题命制的出发点和根源，命题人匠心独具的重要体现就是最终以教材为命题的依归，所以该试题的命制也依托于教材.

1)北师大版高中数学《选修2－1》70页第8题和91页圆的压缩

△ABC 的两个顶点A，B 的坐标分别为(－6，0)，(6，0)，边AC，BC 所在直线的斜率之积为，求顶点C 的轨迹方程，并画出草图.

2)人教A 版《选修2－1》第41页例2以及第50页B 组第1题

在圆x2＋y2＝4上任取一点P，过点P 作x 轴的垂线段PD，D 为垂足，当点P 在圆上运动时，线段PD 的中点M 的轨迹是什么? 为什么?

通过对上述教材中的问题进行分析与探究，发现可以将椭圆通过仿射变换得到圆.由于圆具有许多优美又简洁的性质，体现了数学的简单美、严谨美、对称美、和谐美，故椭圆中也具有类似的性质.换句话说，与椭圆相关的问题由仿射变换可以将椭圆转化为圆，结合圆的性质求解问题可以大大降低运算量，节省运算时间，也在一定程度上拓宽了研究问题的视野.

3 寻根探源

“前车之鉴，后事之师.”借鉴历年真题可以给予我们很多启迪.高考试题来源于教材且高于教材，很多高考试题的背后，都凝聚了命题者的艰辛与心智.调研考试试题命制的灵感就是在历年真题的体会和研究中产生的.

题目(2015 年全国卷Ⅱ理20)已知椭圆C：9x2＋y2＝m2(m＞0)，直线l不过原点O 且不平行于坐标轴，l与C 有两个不同的交点A，B，线段AB 的中点为M.

(1)证明：直线OM 的斜率与直线l 的斜率的乘积为定值；

命题意图本题主要考查与椭圆弦的中点有关的结论、定值、椭圆的性质和直线与椭圆的位置关系，考查数形结合、分类讨论思想，考查逻辑推理和数学运算等核心素养.试题的第(2)问是个开放问题，考查学生的创新能力和解决开放性问题的策略与经验.

如图1，通过几何画板探究，发现直线OM 的斜率与直线AB 的斜率的乘积为定值.

图1

设A(x1，y1)，B(x2，y2)，M(xM，yM)，则x1＋x2＝2xM，y1＋y2＝2yM，对于椭圆而言，由于A，B 两点在椭圆上，则即，可以推导出

图2

设直线l：y＝kx＋b(k ≠0，b ≠0)，A(x1，y1)，B (x2，y2)，M(xM，yM)，仿 照 上 述 推 导过程易知kABkOM＝－9.

图3

4 解法探究

图4

解法1令B(x1，y1)，C(x2，y2)，则A(－x2，－y2)，

当直线AB 的斜率存在时，设直线BC：y＝kx＋m(k≠0)，由得(2k2＋1)x2＋4kmx＋2m2－8＝0，所以x1＋x2＝所以，所以

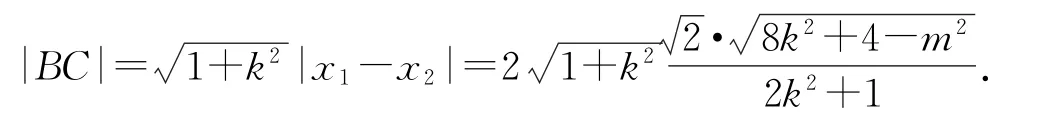
又因为点(0，0)到直线y＝kx＋m 的距离为d＝

解法2令A(x1，y1)，B (x2，y2)，则C (－x1，－y1).

当直线AB 的斜率不存在时，则BC 的斜率为0，此时S△OBC＝.

图5

当直线AB 的斜率存在时，设直线AB：y＝k(x－2)，由得

所以S△OBC的最大值为.

该解法采用化归转化思想，因为△OBC 的面积与△OAB 的面积相等，故可以将△OBC 的面积转化为△OAB 的面积求解，根据分割法可 知，S△OAB＝S△OFB＋S△OFA＝×|OF|·|y1－y2|，得出面积的求解形式后，利用比较判断，最大值在斜率不存在时取到.

解法3学生使用基本不等式求解最值的方法，如果对基本不等式的理解比较薄弱，则我们还可以利用函数的单调性求解.

所以S△OBC的最大值为.

解 法4令A(x1，y1)，B(x2，y2)，则C(－x1，－y1)，设直 线AB：x ＝ty ＋2，由可 得(t2＋2)·y2＋4ty－4＝0，所以

图6

当且仅当t＝0时，即直线AB 垂直于x 轴时，△OBC面积取得最大值.

设 直 线 方 程 为x ＝ty ＋2，利 用S△OAB＝S△OFB＋S△OFA＝|OF|·|y1－y2|求解面积，得出面积的求解形式后，利用基本不等式求解.

解法5由解法4知.由三角形面积向量公式，知

当且仅当t＝0时，即直线AB 垂直于x 轴时，△OBC面积取得最大值.

图7

解法6如图7所示，由椭圆的第二定义可知|AF2|＝a＋ex1，|BF2|＝a＋ex2，推导得出|AB|＝设直线AB 的倾斜角为θ，所以得所以当且仅当sinθ＝1 时，即直线AB 垂直x 轴时，△OBC 面积取得最大值.

解法7构造仿射变换，则椭圆＋转化为x′2＋y′2＝8，如图9所示，则S△OAB＝，欲求S△OAB的面积，只需要求解S△OA′B′的面积即可，设直线A′B′的方程为x′＝my′＋2，所以，所以

当且仅当m ＝0 时，即直线A′B′垂直于x 轴时，△OA′B′面积取得最大值即S△OBCmax＝.

图8

图9

该解法利用仿射变换将椭圆的相关问题转化为圆中的相关问题，使问题变得简单，优化计算，节约时间.

试题求解的过程中都绕不开迅速且准确地找到运算对象、探究运算思路、选择运算方法、准确求解运算结果，然而高中教师普遍认为应重视数学思想方法的教学，而忽视了对学生运算能力的培养，导致学生在解题时出现“会而不对，对而不全”的现象.因此，教师要转变观念，重视对学生数学运算素养的培养.教师应引导学生从运算对象的理解、运算法则的掌握、运算思路的探究、运算方法的选择和运算背景的变换等入手，合理设计运算教学，将数学运算素养落实到每节课，着力培养学生的数学运算素养.