对一道福建省质量检测试题的探究

福建省仙游第一中学(351200) 林碧霞

2020年福建省高三毕业班质量检查测试理科试题第19题如下:

题目已知椭圆=1(a＞b＞0)的焦距为直线l1:x=4 与x轴的交点为G,过点M(1,0)且不与x轴重合的直线l2交E于点A,B,当l2垂直x轴时,∆ABG的面积为

(1)求E的方程;

(2)若AC⊥l1,垂足为C,直线BC交x轴于点D.证明:|MD|=|DG|.

本题(1)的答案是:E的方程为(2)的内涵丰富,意境深邃,具有进一步探究的价值,可以引导学生对此作深入探究.

1.纵向探究:由特殊到一般的探究

本题(2)的结论表明:直线BC过线段MG的中点显 然,点M(1,0)和直线x=4不是椭圆的焦点和准线,但可视为椭圆E:的“类焦点”和“类准线”.那么,对一般椭圆的“类焦点”F(m,0)(0＜m＜a)和“类准线”能否成立? 经探究,可得

命题1.1已知椭圆过定点M(m,0)(0＜m＜a)且不与x轴重合的直线l交椭圆E于点A,B,定直线与x轴的交点为G,过点A作直线l1的垂线,垂足为C,直线BC交x轴于点D,则|MD|=|DG|.

证明设直线l的方程为x=hy+m,与椭圆E的方程联立,得b2(hy+m)2+a2y2−a2b2=0,整理得(a2+b2h2)y2+2b2hmy+b2(m2−a2)=0.

又直线BC的方程为令y=0,可得直线BC与x轴交点D的横坐标xD=进而可得

由此即得|MD|=|DG|,证毕.

特别地,当a2=4,b2=1,m=1 时,有|MD|=|DG|.这就是上述试题第(2)小题的结论.

在命题1.1 中,由结论|MD|=|DG|知,直线BC过线段MG的中点即特别地,当m=c时,可得命题1.1 的推论(即文[1]的命题1,其中的字母有所调整):

推论已知椭圆=1(a＞b＞0)的右焦点为F(c,0),过F点的直线l与E交于A,B两点,过点A作直线的垂线,垂足为C,则直线BC恒过定点

特别地,当a2=4,b2=3 时,c=1,直线BC恒过定点同理可得直线AH(H为过点B作直线l1的垂线的垂足)恒过定点即直线AH与BC相交于定点这就是2016年全国高中数学联赛湖南赛区预赛试题题13 第(2)小题的结论:

(1)求椭圆C的方程(答案:椭圆C的方程为1);

(2)连接AE,BD,试探求当直线l的倾斜角变化时,直线AE与BD是否相交于定点? 若是,请求出定点的坐标,并给予证明;否则,说明理由.

2.逆向探究:由原命题到逆命题的探究

命题1.1的逆命题是否成立? 即若|MD|=|DG|,直线BD与直线AC的交点是否在定直线上? 经探究,这个逆命题成立.可得

命题1.2已知椭圆过定点M(m,0)(0＜m＜a)且不与x轴重合的直线l交椭圆E于点A,B,定直线与x轴的交点为G,过点A作直线l1的垂线,垂足为C,若线段MG的中点为D,则直线AC与直线BD的交点在定直线l1上.

证明连结BC,设直线BC交x轴于点D1,据命题1.1 得|MD1|=|D1G|,即线段MG的中点为D1.又由线段MG的中点为D得点D1与点D重合,则直线BD与直线BC重合,由此可得直线AC与直线BD的交点在定直线l1上.证毕.

易知线段MG的中点D的坐标为当m=c时,可得命题1.2 的推论(即文[2]的推广1,其中的字母有所调整):

推论已知椭圆=1(a＞b＞0),点过点F的动直线l与椭圆E交于不同两点A,B,过点A作y轴的垂线l′,则直线l′与直线BD的交点T恒在准线上.

特别地,当a2=25,b2=9 时,c=4,,直线l′与直线BD的交点T恒在准线上.这就是2019届湖北省8 校高三第一次联考理科数学试题题20 第(3)小题的结论:

已知点F(4,0),过点F的动直线l与椭圆交于不同两点M,N,过点M作y轴的垂线l′,试判断直线l′与直线NH的交点是否恒在一条定直线上? 若是,求该定直线的方程;否则,说明理由.

3.横向探究:由椭圆到双曲线、抛物线的探究

以上命题揭示了椭圆的“类焦点”和“类准线”的一个关联性质,那么,双曲线、抛物线是否具有类似性质? 经探究,可分别得到:

命题2.1已知双曲线=1(a＞0,b＞0),过定点M(m,0)(m＞a)且不与x轴重合的直线l交双曲线E于点A,B,定直线与x轴的交点为G,过点A作直线l1的垂线,垂足为C,直线BC交x轴于点D,则|MD|=|DG|.

推论(即文[1]的命题2,其中的字母有所调整)已知双曲线=1(a＞0,b＞0)的右焦点为F(c,0),过F点的直线l与E交于A,B两点,过点A作直线的垂线,垂足为C,则直线BC恒过定点

命题2.2已知双曲线=1(a＞0,b＞0),过定点M(m,0)(m＞a)且不与x轴重合的直线l交双曲线E于点A,B,定直线与x轴的交点为G,过点A作直线l1的垂线,垂足为C,若线段MG的中点为D,则直线AC与直线BD的交点在定直线l1上.

推论(即文[2]的推广2,其中的字母有所调整)已知双曲线=1(a＞0,b＞0),点,F(c,0).过点F的动直线l与双曲线E交于不同两点A,B(可以在不同支),过点A作y轴的垂线l′,则直线l′与直线BD的交点T恒在准线上.

命题3.1已知抛物线E:y2=2px(p＞0),过定点M(m,0)(m＞0)且不与x轴重合的直线l交抛物线E于点A,B,定直线l1:x=−m与x轴的交点为G,过点A作直线l1的垂线,垂足为C,直线BC交x轴于点D,则|MD|=|DG|.

推论(即文[1]的命题3,其中的字母有所调整)已知抛物线E:y2=2px(p＞0)的焦点为F,过F点的直线l与E交于A,B两点,过点A作准线的垂线,垂足为C,则直线BC恒过定点(0,0).

命题3.2已知抛物线E:y2=2px(p＞0),过定点M(m,0)(m＞0)且不与x轴重合的直线l交抛物线E于点A,B,定直线l1:x=−m与x轴的交点为G,过点A作直线l1的垂线,垂足为C,O为坐标原点,则直线AC与直线BO的交点在定直线l1上.

推论(即文[2]的推广3,其中的字母有所调整)已知抛物线E:y2=2px(p＞0),点O(0,0),过点F的动直线l与抛物线E交于不同两点A,B,过点A作y轴的垂线l′,则直线l′与直线BD的交点T恒在准线

下面只证明命题3.1,其余可仿照椭圆的情形证明.

证明设直线l的方程为x=hy+m,与抛物线E的方程y2=2px(p＞0)联立,得y2=2p(hy+m),整理得y2−2phy−2pm=0.设A(x1,y1),B(x2,y2),C(−m,y1),据韦达定理,得y1+y2=2ph,y1y2=−2pm.又直线BC的方程为令y=0,可得直线BC与x轴交点D的横坐标

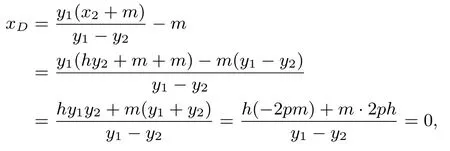
进而可得|MD|=|DG|.命题3.1 得证.

以上通过对一道2020年福建省质量检测试题的纵向、逆向、横向探究,得到了关于圆锥曲线的“类焦点”和“类准线”的一个关联性质及其推论,揭示了问题的内涵和本质.对一些典型试题,仅停留于会解是远远不够的,可以引导学生探究题目背后的知识背景和问题的核心本质,这样才能收到举一反三,以少胜多的学习功效,同时使学生的探究能力和数学学科核心素养得到培养和提升.