一种求解矩阵填充问题的交替共轭梯度最小化法
郭佳浩,闫喜红
(太原师范学院 数学系,山西 晋中 030619)
0 引言
数据缺失下的低秩填充问题是近几年研究热点之一,在机器学习[1]、模式识别[2]、模型缩减[3]等科学工程领域有着重要的作用.一个矩阵填充问题如果没有约束条件,可以有无穷多解,事实上需要填充的矩阵一般具有低秩或者近似低秩的结构.对于低秩矩阵,就可以通过有效的算法准确合理地恢复出原矩阵.由于Fazel在近似低秩矩阵[4]和Candes与Recht在矩阵填充方面做的开拓性工作[5],使得这一问题从理论和算法方面都得到了深入的研究[3,4,6-11].低秩矩阵填充最初是由Candes和Recht提出的,其目的是将仅部分元素已知的采样矩阵精确合理地填充成一个低秩矩阵.矩阵填充和低秩逼近技术依赖于低秩结构的元素之间的依赖关系.在已知矩阵部分元素的前提下,合理精确地寻找与已知项一致的最低秩矩阵,其数学模型可表示为:
(1)
其中Z0∈Rm×n是采样矩阵,Ω是已知样本元素下标集,PΩ是集合Ω上的正交投影.问题(1)是非凸的,直接求解非凸问题非常困难,因此很多学者用它的凸松弛模型取代(1),其凸松弛核范数模型如下:
(2)
其中,‖Z‖*是矩阵Z的核范数.相关的理论已经证明,只要奇异向量与正则基之间存在弱相关性,就可以通过求解上述凸松弛问题(2)得到(1)的解[5].针对凸松弛模型(2),有许多算法(如硬阈值算法、迭代阈值算法等)可以直接进行求解.但是这些算法的实现需要在每次迭代中计算部分奇异值分解(SVD).众所周知,计算奇异值分解(SVD)成本很高.为了避免求解奇异值的高计算成本,Haldar[12]和Wen[13]提出如下分解模型:
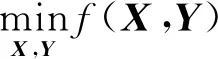
(3)
其中,Z=XY,X∈Rm×r,Y∈Rr×n,r≪min{m,n}.在模型(3)中,Z表示成X∈Rm×r和Y∈Rr×n的乘积,使得确保满足低秩的要求.两个针对模型(3)的特点,一个自然的求解方法就是交替最小化方法,如Power Factorization[12]和LMaFit[13].在这两种交替最小化方法中,变量X和Y交替更新,每一步要精确求解子问题得到X和Y.精确求解子问题的计算量较高.为此,文献[14]设计了交替最速下降法(ASD)和加速交替最速下降方向法(ScaledASD)来求解(3).在此算法中变量X和Y交替更新,且在每一步迭代过程中利用一步最速下降法更新X和Y, 从而提高算法的效率.众所周知,共轭梯度方向较最速下降方向效果好.因此,本文在文献[14]算法的基础上,每一步利用共轭梯度方法来更新X和Y,提出了求解模型(3)的新方法.
本文结构如下,在第一节中介绍了几种相关的交替最小化法;在第二节中,本文提出了4种交替共轭梯度法(ACG);在第三节中将ASD算法和共轭梯度算法进行了数值实验,并进行了比较,验证了交替共轭梯度最小化算法的有效性.
1 交替最小化法
交替最小化法,也称高斯-塞德尔或块坐标下降法.由于其简单性、低内存要求和灵活性被广泛用于求解优化问题.本文考虑的模型(3)的函数是具有两块变量X∈Rm×r和Y∈Rr×n的非凸函数,直接求解较难.注意到模型(3)中关于X和Y都是最小二乘子问题,一个自然的想法就是利用交替最小化方法求解,如算法1(PF)是一种将交替最小化方法应用于模型(3)的矩阵填充算法.
算法1幂因式分解算法(PF).
步一:取初始矩阵PΩ(Z0),初始点X0∈Rm×r,Y0∈Rr×n.
步二:重复计算以下步骤:


直到达到停机标准.
算法1中的每个子问题都是标准的最小二乘问题.作为一种典型的交替最小化方法,算法1的极限点必然是不动点[12].算法1中的最小二乘子问题的求解决定了每次迭代计算成本.为了降低每次迭代子问题的计算成本,文献[13]提出了如下模型:
(4)
其中,投影到Ω上的要求从(3)中的目标移动到线性约束.应用于模型(4)的交替最小化方法给出了低秩矩阵拟合算法(LMaFit).
算法2低秩矩阵拟合(LMaFit).
步一:取初始矩阵PΩ(Z0),初始点X0∈Rm×r,Y0∈Rr×n.
步二:重复计算以下步骤:
3)Zi+1=Xi+1Yi+1+PΩ(Z0-Xi+1Yi+1).
直到达到终止标准.
算法2中的每一步迭代中先固定Z,通过求解最小二乘问题,LMaFit不断地更新X和Y.注意LMaFit中的最小二乘子问题有显示表达式,而可以精确求解,降低了PF算法中的每次迭代计算成本.但是子问题求精确解,计算成本仍很高.为了改进计算效率,文献[14]采用单步沿梯度下降方向的直线搜索代替求解最小二乘法问题,并给出如下交替最速下降算法(ASD算法)[14].
算法3交替最速下降算法(ASD).
步一:取初始矩阵PΩ(Z0),初始点X0∈Rm×r,Y0∈Rr×n.
步二:重复计算以下步骤:
2)Xi+1=Xi-txifYi(Xi).
4)Yi+1=Yi-tyifXi+1(Yi).
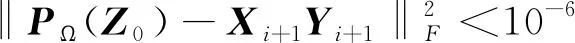
2 交替共轭梯度最小化法
共轭梯度法是各种优化算法中非常重要的一种,最早是由Hestenes和Stiefle[15]在解决大规模线性方程组问题时提出来的,在他们的基础上Fletcher和Reeves(1964)将其引入到了非线性最优化问题中,创立了非线性共轭梯度法.共轭梯度法是一个典型的共轭方向法,其中每一个搜索方向都是互相共轭的.该方法的基本思想是基于前一迭代点的搜索方向对当前迭代点的负梯度方向进行修正来产生新的搜索方向,换言之,搜素方向是当前迭代点的负梯度方向与前一搜索方向的线性组合即:
dk=-gk+βk-1dk-1,
其中,dk是当前点的搜索方向,gk是当前点的梯度,dk-1是前一迭代点的搜索方向.共轭梯度法是介于最速下降法与牛顿法之间的一种方法,它仅利用了一阶导数的信息,既弥补了最速下降法收敛慢的不足,又克服了牛顿法需要存储和计算Hesse矩阵并求逆的缺点.由于这种方法不需要矩阵存储、稳定性高、又有较快的收敛速度和二次终止性等优点.目前在实际问题中已经得到广泛的应用.根据参数βk-1的多种表述形式有如下四种常用的共轭梯度算法.
算法4共轭梯度法(ACG).
步一:取x0∈Rn和终止参数ε≥0.计算g0,d0=-g0.
步二:如果‖gk‖≤ε,算法终止;否则进行下一步.
步三:重复计算如下步骤:
xk+1=xk+αkdk,dk+1=-gk+1+βkdk,其中αk是步长,βk-1可由如下四种公式计算:


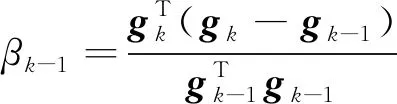
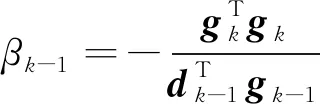
直到满足停机准则.
将此方法应用到模型(3)的子问题中,基于βi的四种计算方法,建立了交替共轭梯度法,其中,βi的四种计算方法如下:


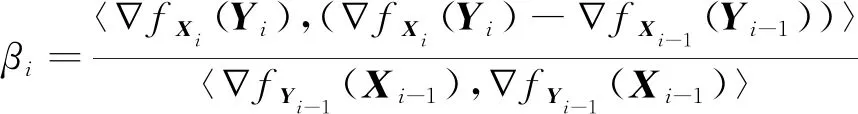

下面详细介绍四种交替共轭梯度法.
算法5交替共轭梯度法1(ACG-CW算法),β是由Crowder-Wolfe公式计算.
步一:取PΩ(Z0),X0∈Rm×r,Y0∈Rr×n和终止参数ε.
X1=X0-tx0fY0(X0),
Y1=Y0-tY0fX1(Y0),
令dx0=-fY0(X0),dY0=-fX0(Y0).
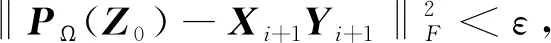
i=2,3,…

Xi+1=Xi+tXidXi,

算法6交替共轭梯度法2(ACG-FR算法),β是由Fletcher-Reeves公式计算
步一:取PΩ(Z0),X0∈Rm×r,Y0∈Rr×n和终止参数ε.
X1=X0-tx0fY0(X0),
Y1=Y0-tY0fX1(Y0),
令dx0=-fY0(X0),dY0=-fX0(Y0).
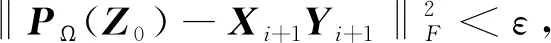
i=2,3,…
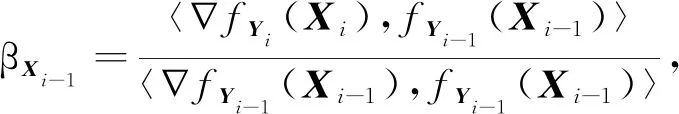
Xi+1=Xi+tXidXi,
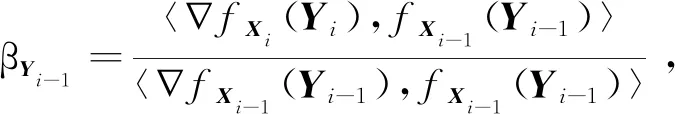
算法7交替共轭梯度法3(ACG-PR算法),β是由Polar-Ribiere公式计算.
步一:取PΩ(Z0),X0∈Rm×r,Y0∈Rr×n和终止参数ε.
X1=X0-tx0fY0(X0),
Y1=Y0-tY0fX1(Y0),
令dx0=-fY0(X0),dY0=-fX0(Y0).
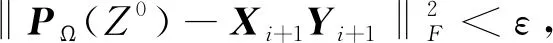
i=2,3,…

Xi+1=Xi+tXidXi,

算法8交替共轭梯度法(ACG-D算法),β是由Dixon公式计算.
步一:取PΩ(Z0),X0∈Rm×r,Y0∈Rr×n和终止参数ε.
X1=X0-tx0fY0(X0),
Y1=Y0-tY0fX1(Y0),
令dx0=-fY0(X0),dY0=-fX0(Y0).
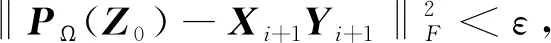
i=2,3,…
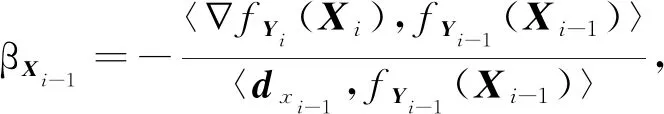
Xi+1=Xi+tXidXi,

3 数值实验
在本小节中,我们通过数值实验将文献[14]中的ASD算法与我们的ACG-CW算法、ACG-FR算法、ACG-PR算法、ACG-D算法进行比较.这里所有的数值实验均是在MATLAB(R2013a)中进行的,机器精度为10-64,机器类型为英特尔核2.4 GB.我们的矩阵也是在相同的实验环境中随机产生的,矩阵的维数从500到1 000,秩取10和15,停机精度为10-4,采样率为10%,运行时间以秒记录.最大迭代次数为1 000,数值结果如表1.
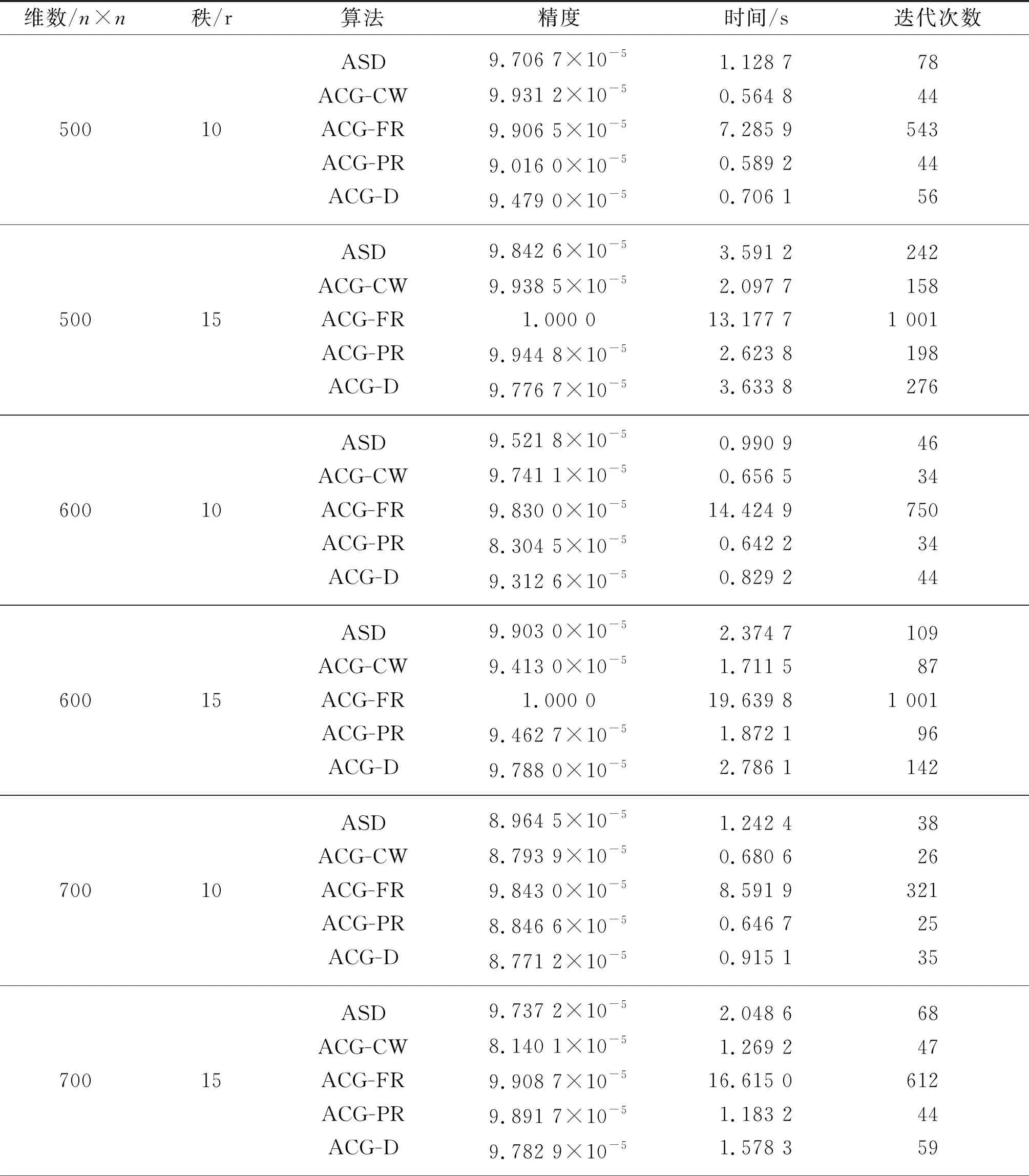
表1 ASD算法与ACG的四种算法的比较
通过表1中数值实验结果,四种共轭梯度算法中ACG-CW和ACG-PR比ASD的迭代次数少,计算时间短.ACG-FR算法和ACG-D算法的优势在于大大提高了精度.因此,矩阵填充的交替共轭梯度法从精度、迭代次数、运行时间方面优化了之前的交替最速下降法.
4 结论
本文针对矩阵填充这个热点问题,基于分解模型,建立一种求解矩阵填充问题的共轭梯度交替方向最小化算法.由于现有的算法大都需要计算矩阵的奇异值分解,计算量较大,计算成本较高,为了避免高成本计算,本文利用分解模型提出交替共轭梯度算法,且把此算法应用到随机产生的低秩矩阵填充问题中,数值结果表明了共轭梯度交替算法的可行性与优越性.

