2020年高考山东卷圆锥曲线试题研究*
广东省中山纪念中学(528454) 胡光裕 鞠火旺
一、呈现试题,分析求解
题目(2020年高考山东卷第22 题)已知椭圆C:的离心率为且过点A(2,1).
(Ⅰ)求C的方程;
(Ⅱ)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明: 存在定点Q,使得|DQ|为定值.
本题考查了椭圆方程的求法,直线与椭圆的位置关系中直线过定点问题,涉及到数形结合、分类讨论的思想;考查了学生的逻辑推理能力、转化与化归能力以及综合运算能力.

图1
试题设置了两问,梯度明显,具有很好的区分度.第(Ⅰ)问求椭圆方程,属于常规问题;第(Ⅱ)问可谓“新瓶装旧酒”,只要考生熟悉“手电筒”模型(过椭圆上一点A作AM⊥AN,直线AM、AN分别交椭圆于M,N两点),则直线MN恒过定点P,又点A(2,1)是椭圆上的定点,因此线段AP的长度为定值.于是在RtΔADP中,中线QD的长度等于斜边AP的一半,因此满足题目要求的定点Q存在,它就是斜边的中点.至此这道题就转化为证明直线MN恒过定点,这是本题的关键所在.
解(Ⅰ)C:过程从略.以下求解第(Ⅱ)问.
(1)若直线MN的斜率不存在,设其方程为x=x0,则M(x0,y0),N(x0,−y0),因为所以(x0−2,y0−1)·(x0−2,−y0−1)=0,即(x0−2)2+(1)=0,又代入解得或x0=2(舍),此时直线方程为x=
(2)若直线MN的斜率存在,设为y=kx+m,M(x1,y1),N(x2,y2),由得(1+2k2)x2+4kmx+2m2−6=0,由韦达定理又

故
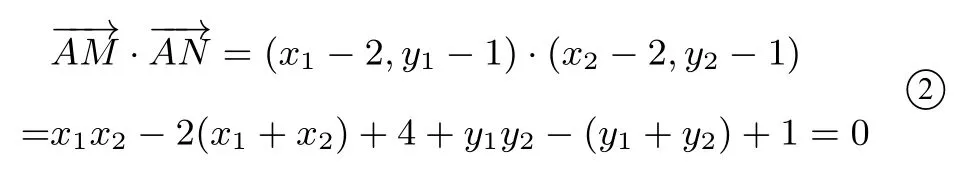
将①代入②得

又因为AD⊥MN,D为垂足,所以ΔADP为直角三角形,且∠D为直角,因此当点Q为斜边AP的中点时,|DQ|为定值,其值等于
二、推广结论,揭示本质
本题作为一道压轴题,第二问的本质是考察直线MN过定点.那么当点A是椭圆上的任意一点且对于任意常数当kAM ·kAN=δ时,直线MN是否仍过定点呢? 如图2 所示,在TⅠ-Nspire 中探究发现结论仍然成立,实际上,有如下的一般性的结论:
结论Ⅰ[2]已知点A(x0,y0)是椭圆b >0)上任意一点,直线AM、AN与椭圆C相交于M、N两点,若kAM ·kAN=δ,其中则直线MN过定点

图2
证明在文[2] 和文[3] 中,已经给出了结论Ⅰ详尽的证明,我们另辟蹊径,考虑用双直线系的方法[1]证明它.为此,不妨设直线AM的方程为y −y0=k1(x −x0),即(k1x −y)+(y0−k1x0)=0,同理直线AN的方程为(k2x −y)+ (y0−k2x0)=0,那么双直线方程[2][(k1x −y)+(y0−k1x0)][(k2x −y)+(y0−k2x0)]=0 是直线AM、AN上一切点所满足的方程,其图像见图3,整理此方程得

图3


注意到A(x0,y0)∈ C,于是=1,故有上式进一步简化为(k1+k2)(x −x0)(y −y0)−2δx0(x −x0)−2y0(y −y0)=0,由于双直线方程表示的曲线与椭圆共有A(x0,y0)、M、N三个交点,因此x=x0满足此式,从而得到
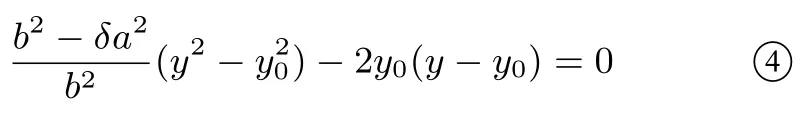
类似地,由y2=b2−及k1k2=δ,③式可整理为

综上所述,直线MN恒过定点

特别地,当AM⊥AN即kAM ·kAN=−1 时,直线MN仍过定点,故有如下推论Ⅰ成立.
推论Ⅰ已知A(x0,y0)是椭圆1(a >b >0)上任意一点,直线AM、AN与椭圆C相交于M、N两点,且AM⊥AN,则直线MN恒过定点
推论Ⅱ已知椭圆C:=1(a >b >0),点A(x0,y0)是椭圆上任意一点,直线AM、AN与椭圆C相交于M、N两点,且kAM · kAN=δ,其中过点A作AD⊥MN,垂足为D,则D点的轨迹是以为圆心,为半径的圆.

图4
证 明因为A(x0,y0)∈ C且由结论Ⅱ知是定点(当A点固定时),又AD⊥MN,于是点D的轨迹是以AP为直径的圆,记圆心O(x,y),半径为r,则

且
化学植筋技术,因为其所使用的设备简单,并且操作过程简易,效率高,投入少,在建筑行业中的使用越来越广泛。本文所述的水利工程中植筋技术的应用取得的使用效果非常良好,在今后的工程当中将会被广泛推广。

于是结论得证,点D的轨迹见图4.
三、横向拓展,深度剖析
结论Ⅱ已知椭圆C:=1(a >b >0),点A(x0,y0)是椭圆上任意一点,直线AM、AN与曲线C相交于M、N两点,若kAM+kAN=δ(其中δ /=0),则直线MN过定点
文[2]和文[3]中已给出了该结论的详细证明,类似结论Ⅰ,也可以用双直线系的方法证明之,这里从略.
推论Ⅲ已知A是椭圆C:=1(a >b >0)的右顶点,直线AM、AN与曲线C相交于M、N两点,若kAM+kAN=δ(其中δ /=0),则 直线MN过定点
证明由于点A(a,0)是椭圆的右顶点,故只需在结论Ⅲ中取x0=a,y0=0 便得直线MN过定点此外,在这种特殊情况下,我们也可以简证如下.
设AM的方程为y=k1(x −a),即k1x −y −k1a=0,同理AN的方程为k2x −y −k2a=0,于是过A、M、N三点的双直线方程为[(k1x −y)−k1a][(k2x −y)−k2a]=0,展开整理得


由于双直线与椭圆共有A、M、N三个交点,其中xA=a,而直线MN不过点A,所以x /=a,因此⑥式可化简为k1k2(x −a)−(x+a)−δy=0,该式对任意k1、k2∈ℝ 恒成立,为此取x=a得×2a −δy=0,解得这表明直线MN过定点T
四、应用举例,回归真题
例题(2017年高考全国Ⅰ卷理科第20 题)已知椭圆=1(a >b >0),四 点P1(1,1),P2(0,1),中恰有三点在椭圆上.(1)求椭圆的方程;(2)如图5 所示,设直线l不经过点P2且与椭圆C相交于A、B两点,若直线P2A与直线P2B的斜率之和为−1.证明: 直线AB过定点.

图5
证明(1)椭圆的方程为+y2=1,过程从略;(2)设直线P2A的方程为y=k1x+1,即k1x −(y −1)=0,同理直线P2B的方程为k2x −(y −1)=0,构造过P2、A、B三点的双直线方程[k1x −(y −1)][k2x −(y −1)]=0,即


由于双直线与椭圆共有P2、A、B三个交点,其中yP2=1,而直线AB不过点P2(0,1),因此y /=1,从而4k1k2(1+y)−x+(1−y)=0 对任意的k1、k2恒成立,于是取y=−1,代入得−x+2=0,解得x=2,这表明直线AB恒过定点(2,−1).
变式条件不变,若直线P2A与直线P2B的斜率之积为证明: 直线AB过定点.
证明注意到k1k2=δ,将⑦式与椭圆联立,同上可得

对任意的k1、k2恒成立,为此取x=0,代入得4δ(1+y)+(1−y)=0,解得y=这表明直线AB恒过定点
此外,本文重点讨论的2020年山东卷第22 题,类似结论Ⅰ的证明方式,同样可以得到直线MN恒过定点这里就不再重复了.
从上面的计算过程中不难发现,用双直线方程和椭圆方程联立求解要比采用常规的处理方式(韦达定理)简单;同时,这种方法充分展现了双直线方程的理论价值: 在“手电筒”模型(过椭圆上一点A作直线AM、AN分别交椭圆于M,N两点)中,通过消元(得到的③式k1·k2x2−(k1+k2)(x −x0)(y −y0)+y2−2y0y −2k1·k2x0x++k1·k2=0)很好地解释了为什么只有当直线AM和AN的斜率之积或者斜率之和为定值时,直线MN才可能过定点.
此外,当两直线AM和AN的斜率之差或者商为定值时,直线MN并不过定点,而是形成包络线[4].
在双曲线和抛物线中也有非常类似的结论[5],限于篇幅,我们就不再一一赘述了.

