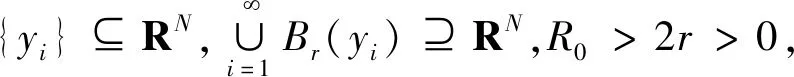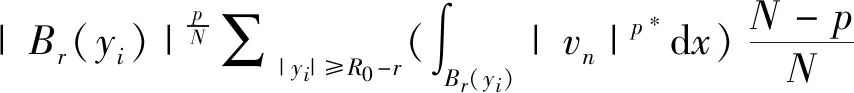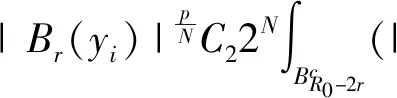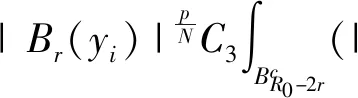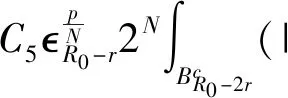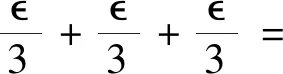一类Sobolev空间紧嵌入定理
林振生
(1.福建工程学院 计算机科学与数学学院,福建 福州 350118;2.福建师范大学 数学与信息学院,福建 福州 350117)
为纪念前苏联科学家 Sobolev,学者们将一类函数空间命名为 Sobolev空间,它是寻找椭圆方程解存在性常用的基本工具[1]2,[2]1。有关 Sobolev 空间有大量的研究工作及应用场景[3-5]。郭玉霞等人[5]研究了带有某类深井位势的双调和方程极小能量解的存在性。Liu等人[4]在更一般位势假设下,研究某类非线性SchrÖdinger方程解的存在性,提及一类比普通深井位势更弱的位势函数,工作空间具有一定的紧性嵌入性质。但未给出该结论的证明。这结论也出现在文献[6]引理3.4,Zou[6]45利用命题1.13(有界区域上的Sobolev 嵌入定理)及命题1.16(Gagliardo-Nirenberg 不等式)给出这一紧嵌入定理的详细证明。而为能利用锥上的上同调环绕变分方法解决一类带有位势函数的p-Laplace方程非平凡解的存在性问题,Liu[3]给出更弱意义下的 Sobolev 空间紧嵌入定理。近十年来,带不同位势函数的Sobloev空间及其应用一直是学者们关注的问题,是否存在比文献[4-6]中位势函数更弱的位势函数?如果存在,那么在研究p-Laplace方程非平凡弱解存在性时,这类更弱位势函数的Sobolev空间是否也存在紧嵌入定理?本文力图论证带更弱位势函数的一类Sobolev函数空间存在紧嵌入定理。
1 问题描述及主要结果
过去学者们常使用满足如下(V0)、(V1)条件的位势函数V(x):
在深井位势函数环境下, 郭玉霞等[5]人研究了带深井位势的双调和方程极小能量解的存在性。而在文献[7]中,Bartsch等人也在(V0)、(V1′)假设下,研究下列非线性SchrÖdinger方程解的存在性
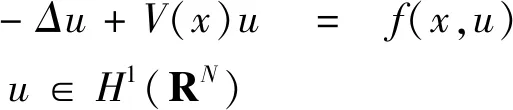
(1)
其中,(V1′)对于任意的b∈R,m({x|V(x)≤b})<+
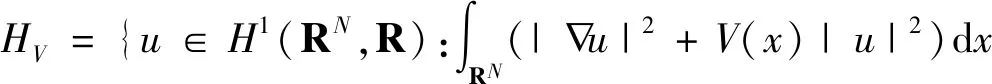
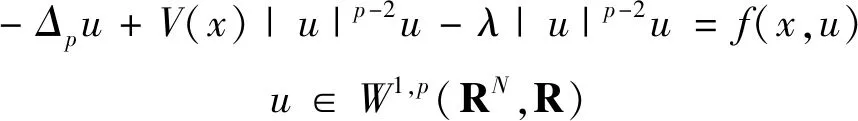
(2)
Bartsch等在文献[8]中提出一类带有(V2)条件的位势函数:
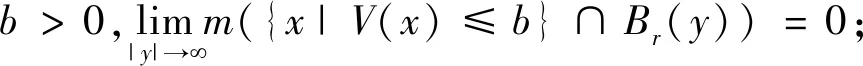
而Liu等在文献[4]第三节中研究一类带有(V2)条件的位势函数的非线性SchrÖdinger方程解的存在性,但未给出紧嵌入定理的证明。以下给定两个条件记号(V1″)、(V2′):
(V1″)对于任意的b∈R,{x|V(x)≤b}是有界的;
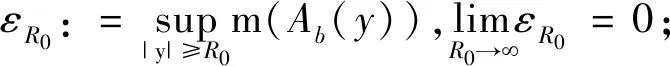
其中,Ab(y):={x|V(x)≤b}∩Br(y)。
可得:条件(V1)与(V1″)等价;条件(V2)和(V2′)也等价;条件(V1′)比(V1″)更弱;条件(V2′)比(V1′)更弱。
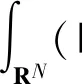
假设位势函数V(x)满足(V0)、(V2)两个条件,论证带有这类更弱位势函数的一类Sobolev空间存在紧嵌入定理。
定理1.1假设(V0)、(V2)成立,那么,X→→Lt(RN),对于一切的2≤p≤t 由于(V0)条件的假设及X空间的定义,借鉴文献[9]附录A,可知X是一个自反、可分的Banach空间。同时,存在连续嵌入结论:X→Lt(RN),对于一切的 2≤p≤t 注记1.1 假设(V0)、(V1′)成立,那么,X→→Lt(RN),对于一切的2≤p≤t 注记1.2 假设(V0)、(V1)成立,那么,X→→Lt(RN),对于一切的2≤p≤t 注记1.1是文献[3]引理2.1,由于定理1.1中V(x)条件更弱,因此它是更一般的结论。除此之外,定理1.1允许p≥2且V(x)条件也更弱,推广了引理3.4[6]45,这正是注记1.2。同时发现,存在满足(V1)条件却不满足(V2)条件的函数,如:V(x)=|x|2,V(x)=C+|x|2,其中C是一个正的常数。而由于定理1.1条件更弱,且不仅仅包含p=2的情形,还包含p>2,面临新的困难,需要新的处理技巧及新的工具。 除特别说明外,Ci(i∈N)表示不同的常数。描述空间两者关系时,→表示连续嵌入;→→表示连续紧嵌入;⇀表示弱收敛;N表示全体自然数组成的集合;R表示全体实数组成的集合;RN表示N维欧几里得空间;|·|p表示Lebesgue 空间Lp(RN)的标准范数。 给出两个准备引理,分别是插值不等式(HÖlder不等式)及有界区域上的紧嵌入定理(Rellich-Kondrachov定理): 引理2.1[2]27假设1≤r (3) 定理1.1的证明。 假设{un}是X中一有界序列,un⇀u在X中成立,则un→u在Lt(RN),对一切的2≤p≤t 其中,vn:=un-u。由于{vn}是Lp*(RN)中有界序列,而vn→0在Lp(RN)中成立,推得vn→0在Lt(RN)中成立。也就是说对于一切的2≤p≤t 以下证明:un→u在Lp(RN)成立。 (4) 再由引理2.2,有W1,p(BR0)→Lp*(BR0)。于是,存在一个正数C1,使得对于u∈W1,p(BR0),有 |u|Lp*(BR0)≤C1‖u‖W1,p(BR0) 联立这个连续嵌入不等式以及式子 (4) 及{vn}有界性,可推得 (5) 除此之外,还有 (6) 因为(V0)、(V2)成立,{vn}是X中的有界序列。因此,结合式(5)和(6),对于任意>0,容易推得以下结果 对于足够大的b、R0成立。 故,un→u在Lp(RN)中成立,证毕。 注记1.1的证明: 由于条件(V2)比条件(V1′)更弱,仿照定理1.1的证明,容易得到该注记的证明。 注记1.2的证明: 由于条件(V2)比条件(V1)更弱,仿照定理1.1的证明,也同样容易得到该注记的证明。2 基本引理
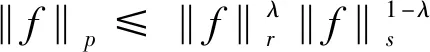
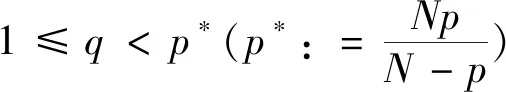
3 主要定理证明