带双参数的拟五次Said-Ball 曲线及其应用*

王成伟 张卷美

1. 北京服装学院，北京市 100029

2. 北京电子科技学院，北京市 100070

三次Ball 曲线[1－2]于1974 年被A.A.Ball 定义以来，有许多学者深入地研究了Ball 曲线。Said[3]推广了Ball 曲线，形成了Said-Ball 曲线。Ball 曲线的许多性质跟Bézier 曲线是比较类似的[4－5]，但是Ball 曲线的计算效率要比Bézier 曲线高。 若控制多边形固定不变，Ball 曲线和Bézier 曲线都有形状不能改变的缺陷，因此许多学者就提出了在Ball 扩展曲线中嵌入形状参数的方法[6－11]。 文献[6－9] 通过嵌入一个形状参数对三次Ball 曲线进行了扩展， 文献[8－10]分别扩展了四次和五次Said-Ball 曲线，它们的扩展曲线中只有一个形状参数，因此用一个形状参数来改变曲线的形状是有局限性的。 文献[11－12]分别讨论了含有两个形状参数五次Said-Bal和拟六次Said-Ball 曲线的扩展问题。

本文讨论了拟五次Said-Ball 曲线，在基函数构造时，增加了两个形状参数λ、μ，基函数具有对称性。 本文讨论的拟五次Said-Ball 曲线，与文献[11]的构造方法不同，文献[11]中的基函数有5 个，其实就是四次Said-Ball 曲线的扩展；而本文中的基函数有6 个，也就是五次Said-Ball 曲线的扩展。 五次Said-Ball 曲线和文献[10]中的第2 种扩展曲线都是本文拟五次Said-Ball 曲线的特例，具有一定的广泛性。 还给出两条相邻的拟五次Said-Ball 曲线段拼接的条件，实例显示本文所构造的曲线是有效的。

1 拟五次Said-Ball 曲线的构造

1.1 构造基函数以及其性质

定义1 令

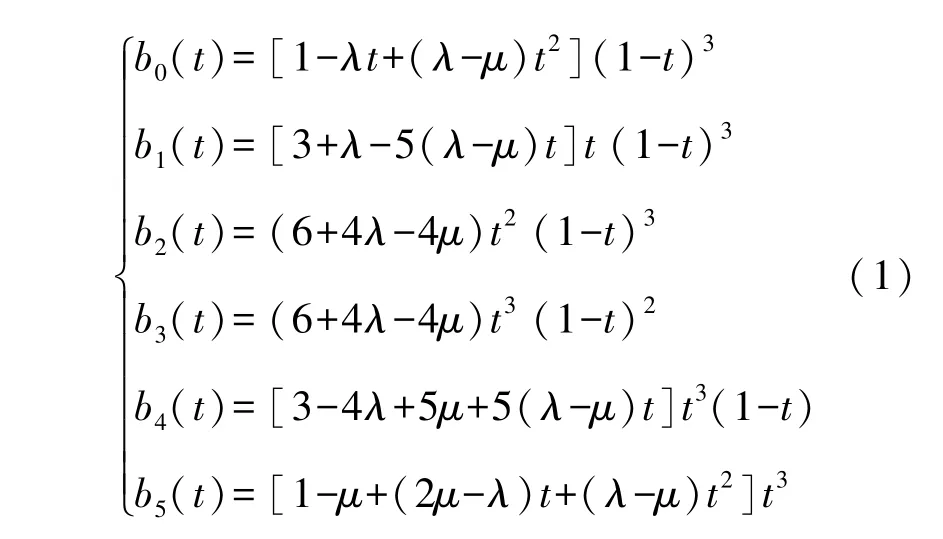
其中，t∈[0，1]、λ∈[－0.5，0.75]、μ∈[0，1]。 则(1)式称为带双参数λ和μ的拟五次Said-Ball 的基函数。

λ＝0.75、μ＝1 时基函数所绘的图形见图1。

图1 拟五次Said-Ball 基函数所绘制的图形

拟五次Said-Ball 的基函数拥有性质如下:

性质1 非负性及权性

性质2 对称性

对于任意的t∈[0，1]， 总有bi(t)＝b5－i(1－ t)，i＝0，1，2，3，4，5。

性质3 端点性质

b′0(1)＝b″0(1)＝b′1(1)＝b″1(1)＝b′2(1)＝b″2(1)＝b′3(1)＝0。

性质4 单峰性

在闭区间[0，1]上，固定λ∈[－0.5，0.75]和μ∈[0，1]，每一个的基函数都有唯一一个的最大值。

性质5 退化性

拟五次Said-Ball 基函数，当λ＝0、μ＝0 时，就退化变为五次Said-Ball 曲线的拥有基函数；当λ＝2β、μ＝1 时，就是参考文献[10]中的第2种曲线所拥有的基函数。

性质6 对参数λ、μ 的单调性

当t∈[0，1]，b0(t) 与b5(t) 都是分别关于λ、μ 的单调递减的，b2(t) 与b3(t) 都是关于λ的单调递增的，b1(t) 与b4(t) 都是关于μ 的单调递增的，b2(t) 与b3(t) 都是关于μ 的单调递减的。

1.2 拟五次Said-Ball 曲线的构造及性质

定义2 设控制顶点Pi∈Rd，d＝2，3，i＝0，? 1，2，3，4，5，对任意λ∈[－0.5，0.75]、μ∈[0，1]，令

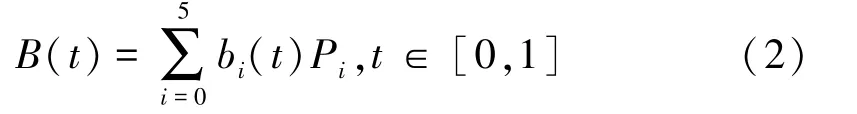
则(2)式称为带有双参数λ、μ 的拟五次Said-Ball 曲线。

显然，拟五次Said-Ball 曲线，当λ＝0、μ＝0时，就是五次Said-Ball 曲线；当λ＝2β、μ＝1 时，就是参考文献[10]中的第2 种扩展曲线。

图2 表示的是双参数λ、μ 取值不同，形成的拟五次Said-Ball 曲线，从下至上(λ，μ) 分别取(－0.5，0)， (0.1，0.5)， (0.75，1)。

图2 3 条拟五次Said-Ball 曲线

根据性质1－6，我们可以得到拟五次Said-Ball 曲线的如下性质:

性质7 凸包性

凸包性是指当控制多边形为凸时，拟五次Said-Ball 曲线为凸的且整条曲线段落在其控制多边形的内部。

根据性质1，这条性质就可以得到。

性质8 对称性

由 控 制 多 边 形P0P1P2P3P4P5和P5P4P3P2P1P0所生成的拟五次Said-Ball 曲线，它们的形状是一样的，但方向是相反。

根据性质2，有:

性质9 端点性质

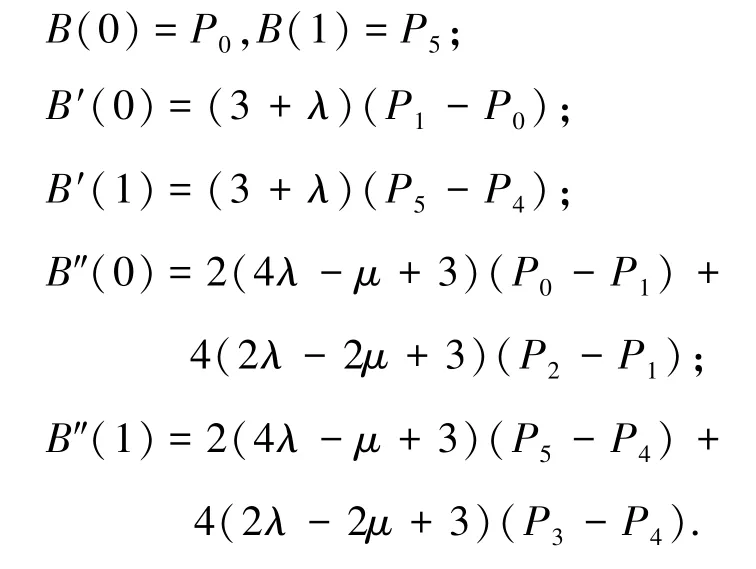
1.3 参数对曲线形状的影响

(1) 固定参数λ＝0.5，当μ 变动时，形成的曲线如图3(a)所示，其中曲线从下到上分别为μ＝0，0.5， 1 的情况。 从图3(a)中可知当λ 固定不变，μ 值越大，曲线与控制多边形就越接近。

(2) 固定参数μ＝0.5，当λ 变动时，所产生的曲线如图3(b)所示，其中曲线从下至上分别为λ＝－0.5，0.1，0.75 的情况。 从图3(b)可知，当μ 值不变，λ 越大曲线与控制多边形就越接近。

2 λ 与μ 在几何上的意义

将(1)式的拟五次Said-Ball 基函数改写如下:

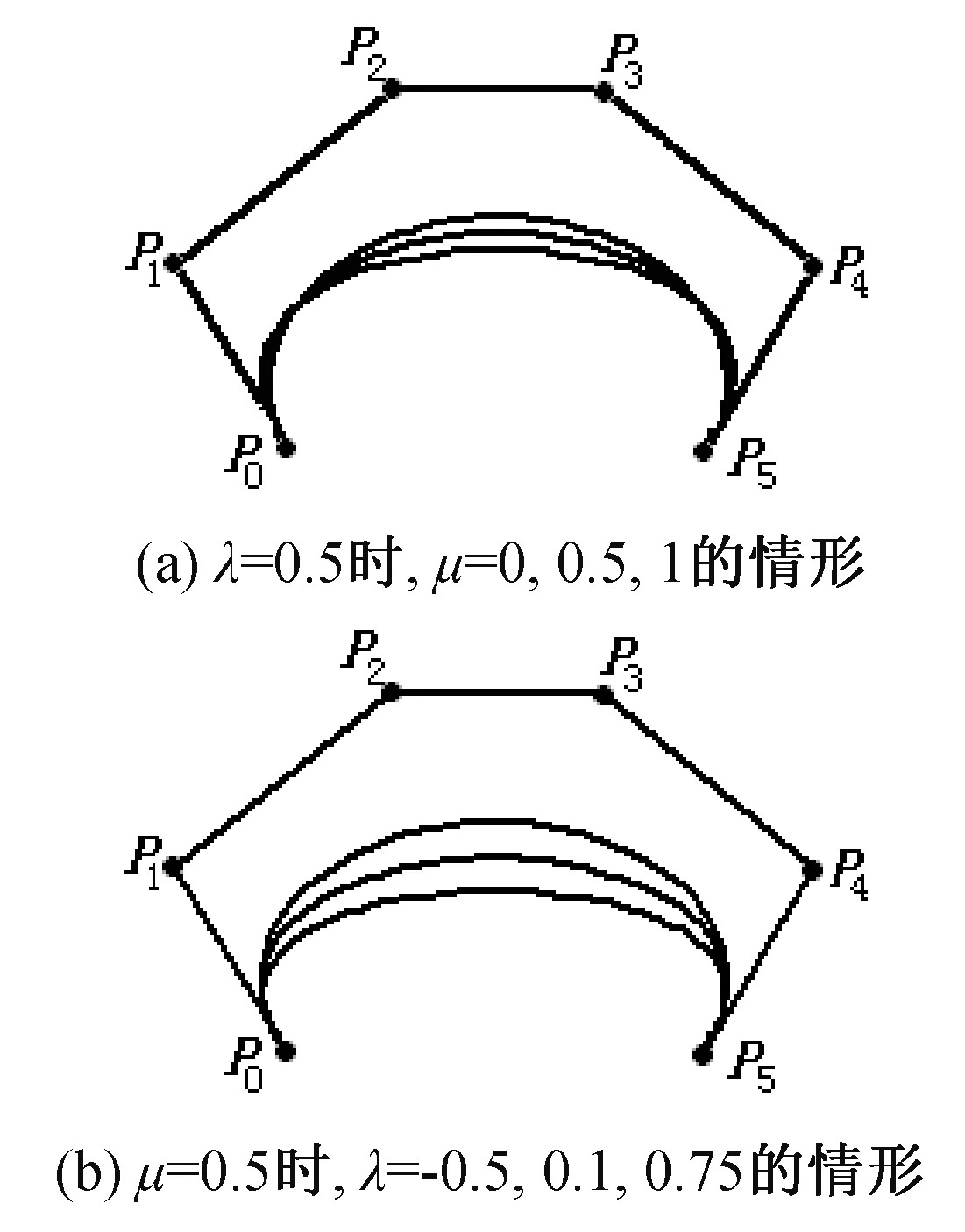
图3 形状参数对曲线的影响

用矩阵b＝MB表示(3)式，其中

若记P＝(P0P1P2P3P4P5)， 则可用矩阵B(t)＝PMB表示拟五次Said-Ball 曲线。 记五次Bézier 曲线的控制顶点为V＝(V0V1V2V3V4V5)，令B(t)＝VB，拟五次Said-Ball 曲线就能被五次Bézier 曲线表示。 则由以上分析可得出，用V＝PM表示它们控制顶点之间的关系，即

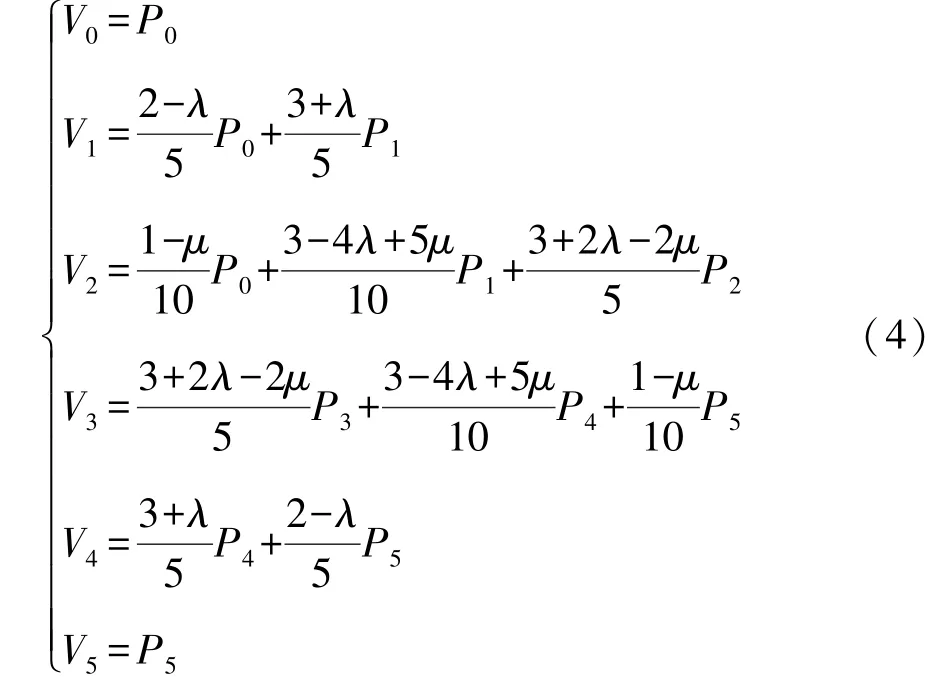
由(4)式可知

3 两条曲线的拼接

即

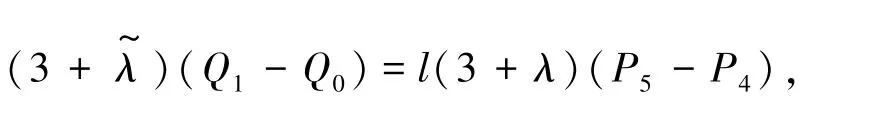
则有:

即有

4 应用举例

4.1 花瓣图形

图4(a)所示，由拟五次Said-Ball 曲线绘制的开曲线形成花瓣图形，参数(λ，μ)从里到外依次为(－0.5，0)，(0，0.4)，(0.4，0.7)， (0.75，1)。 若首末两控制顶点相同时，这样就形成了一条封闭曲线。 图4(b)所示是花瓣由闭曲线形成，参数(λ，μ)从里到外分别为(－0.5，0)，(0，0.4)，(0.4，0.7)， (0.75，1)。

图4 拟五次Said-Ball 曲线绘制的花瓣图形

4.2 衣身基本纸样设计

采用带双参数拟五次Said-Ball 曲线来设计衣身基本纸样，如图5 所示。 可调整形状参数λ、μ，衣身基本纸样设计曲线的形状就会发生相应改变，可以满足不同的个体的要求。

图5 衣身基本纸样设计

5 结束语

本文构造的含有两个形状参数的拟五次Said-Ball 曲线，固定控制顶点时，可以调整曲线的位置和形状，能形成包括五次Said-Ball 曲线，以及文献[10]中的第2 种曲线在内的许多条曲线。 从上面实例可看出，本文所构造的带有双参数拟五次Said-Ball 曲线，更能满足曲线的设计要求。