发展逻辑推理能力需“知行合一”

戴婷婷

摘要：思考复习课上的困惑，提出发展逻辑推理能力需要知行合一.在完善知识结构方面，提出建立下游命题系统和上游命题系统，提炼基本图形;在形成解题策略上，提出把握图形之间的关系，聚合发散性成果和反思解题过程.

关键字 逻辑推理;联想;转化

初中是发展逻辑推理能力的关键期，平面几何是其发展的最佳载体.很多人爱好数学都是从学习平面几何开始的.学生喜欢几何图形的丰富多变，同时又畏惧平面几何的证明，表现为证明思路难以形成和容易想当然，追根究底还是逻辑推理能力上的欠缺.因此，如何通过平面几何有效发展逻辑推理能力值得数学教师深入思考与实践.

1 复习课上的困惑

笔者曾在复习课中让学生证明如下问题：

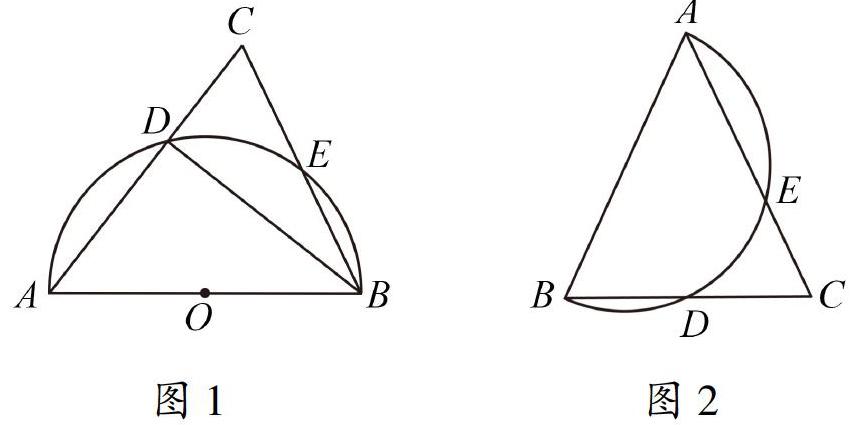
如图1，在△ABC中，AB=AC，以AB为直径的半圆分别交边AC，BC于点D，E，连接BD.求证：点E是BD的中点.

此题来源于教材，原题如下：

如图2，等腰三角形ABC的顶角∠BAC为50°，以腰AB为直径作半圆，交BC于点D，交AC于点E.求BD，DE和AE的度数.

教学困惑 复习课上的证明题只是将原题的图形换一个方向，结果很多学生就想不到证明思路.原题的图形是等腰三角形的底边朝下的标准形式，学生容易联想等腰三角形三线合一的性质.换方向后，学生失去了几何直觉，会想到连结DE去证明BE=DE.如果学过圆内接四边形，学生容易证得∠CDE=∠ABC，进而得到∠C=∠CDE，再得出∠BDE=∠DBE.但现在还没教过，学生想连结DE，利用直角三角形斜边上的中线等于斜边的一半的性质，但一直无法说明点E是BC的中點.为何在课堂上讲过例题，总结过方法，在练习中仍想不出解题思路呢？为什么学生一直想着利用弦等推弧等，却想不到圆周角等转化成弧等？

教学思考 改变图形的方向是一个不容忽视的变式，它足以让学生蒙蔽于表象，想不起先前的解题经验.学生的思维方向较单一，往往利用已有的经验去解题.原题在课堂上让学生证明△CDE是等腰三角形，并且发现斜中点模型.因此，学生首先想到的是连结DE，但发现利用现有的知识不好证明.另外，对数学定理的掌握程度决定了学生优先选择的思维方向.学生对圆心角定理的逆定理比圆周角定理的推论掌握得好，并且弦的位置离弧的位置最近，所以先想到证明弦等.而且学生缺少解题策略，往往走入了死胡同还要一条路走到黑.因此，学生的逻辑推理能力亟待加强，不仅需要知识的储备，方法经验的积累，更需要策略上的指导.

2 完善知识结构

2.1 建立下游命题系统[1]

逻辑推理的一个重要方向是由因导果，即由问题的条件推出相应的结论.这就需要储备与这个条件相关的定理，才能在解决问题时从知识储存库中提取定理，联想对应的结论.学生的知识往往较为零散，需要有意识地进行梳理，可以借助思维导图等工具总结一个条件所能推出的所有结论，这样才能让思维发散，形成多条解题路径.

如例题中的条件“AB=AC”，会触发我们联想等腰三角形的所有性质，由“等腰三角形的底角相等”推出∠ABC=∠C，由“等腰三角形三线合一”想到连结AE，得出高线，角平分线和中线.条件“以AB为直径”让人想到“直径所对的角是直角”，得到∠ADB=90°，或连结AE得到∠AEB=90°.再结合刚才“等腰三角形三线合一”推出BE=CE，∠BAE=∠CAE.再由中间结论“∠BAE=∠CAE”联想到“在同圆或等圆中，相等的圆周角所对的弧相等”，推出点E是BD的中点.只要审题时浮想联翩，读完已知条件的时候，发现结论早已证明完毕.

2.2 建立上游命题系统[1]

解题的另一个重要方向是执果索因，即由问题的结论倒推需要先证明什么.这也需要有意识地对定理进行梳理，借用思维导图总结推出一个结论可以由哪些条件推得.这样在实际解题的时候，就能把结论转化为中间结论，不断转化，直到和已知联系在一起.

如例题中的结论“点E是BD的中点”，促使我们从知识储备库里提取结论是弧等的定理.（1）若想到垂径定理，则需要先证明OE⊥BD，或OE平分BD.根据前面的推理得出的中间结论“∠ADB=90°”，则只需证明OE∥AD即可.要证明OE∥AD，联想平行线的判定方法如“同位角相等，两直线平行”，“内错角相等，两直线平行”，“同旁内角互补，两直线平行”，三角形的中位线和平行四边形的性质.再结合中间结论“∠ABC=∠C”，思考∠OEB与∠ABC的关系，发现由半径相等构造等腰三角形即可得出.（2）若想到“在同圆或等圆中，相等的圆周角所对的弧相等”，即可把结论转化为证明∠BAE=∠CAE.再结合“等腰三角形三线合一”的性质，就能形成解题路径.（3）若联想到圆心角定理的逆定理，则可把弧等转化为证明BE=DE，或∠BOE=∠DOE.若要证明BE=DE，则需先证明∠C=∠CDE.由中间结论“∠C=∠ABC”，思考∠CDE与∠ABC的关系，联想“圆内接四边形的对角互补”即可证明.若要证明∠BOE=∠DOE，则需证明OE∥AD，连结OD，得出∠OAD=∠ADO.证明OE∥AD，还需先证明OE是中位线.由此发现，执果索因如果结合已知条件推出的中间结论，会更容易形成解题路径.

2.3 提炼基本图形

基本图形是心理学上的一种图式.人的短时记忆只有7±2的容量，为了提高头脑的工作效率，可以把定理或解题经验浓缩成基本图形来记忆.基本图形包含了图形的条件和结论，识别出基本图形，便能直接从条件推导出结论，缩短了解题路径的长度.

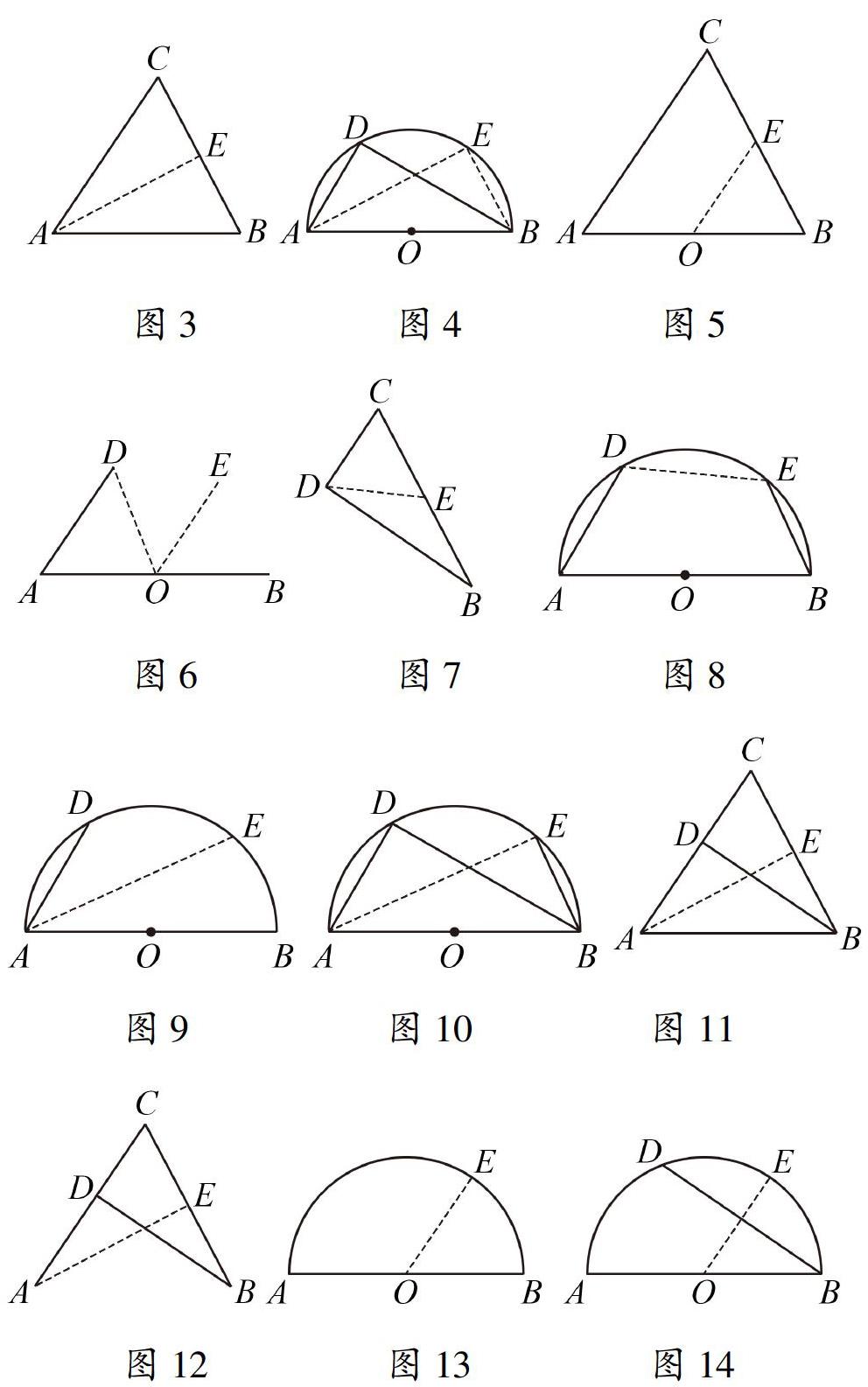
如例题的图形中包含了等腰三角形三线合一模型如图3，直径所对的圆周角是直角模型如图4，中位线模型如图5，双平模型如图6，斜中点模型如图7，圆内接四边形模型如图8，等弧所对的圆周角相等模型如图9，同弧所对的圆周角相等模型如图10，等积法模型如图11，公共角相似三角形模型如图12，半径相等构等腰模型如图13，垂径定理模型如图14.观察出基本图形，就容易将问题的条件转化成中间结论，或将最终结论转化成中间结论.

3.1 把握图形之间的关系

我们教师平时喜欢在解题方法上进行引导，如启发学生思考由条件联想到什么？要证明结论得先证明什么？然而，学生遇到新问题时又常常无从下手.所以，学生更缺乏的是具体问题具体分析的能力，即读图的能力.复杂图形总是由基本图形组合而成，其中的元素常常具有双重角色，读懂了便容易在两种角色之间互相转化.

如例题中的图形是由圆和等腰三角形组合而成，点A，B既是等腰三角形的顶点，又是圆上的点，点E既是底边上的中点又是圆上一点.线段AB既是等腰三角形的腰，又是圆的直径，BD是圆上的一段弦又是等腰三角形腰上的一段高.∠A和∠ABC既是等腰三角形的内角，又是圆周角.读图后，便容易将一个元素放入两个背景图形中考虑.如求线段BD的长就不仅考虑在等腰三角形中用等积法或勾股定理，也要考虑在圆中可以用垂径定理求弦长.计算过程中易于在两个不同背景图形中切换，提高思维的流畅性.

3.2 聚合发散性成果

大多数学生都能从条件推出些中间结论，也都能从最终结论倒推出中间结论，却少有人能真正打通解题路径.这首先与学生的知识结构有关，不少学生思维路径单一，没有联想到与条件相关的其他定理，思维方向比较偏就难以找到中间结论的联系点.所以，平时要让学生把数学定理掌握扎实，养成浮想联翩的习惯.要能以条件和结论为中心，发散地思考出相关的内容.

其次，要根据解题方向聚合发散性成果.从结论出发往往更有目的性，要善于将结论不断转化，直到和中间结论接轨为止.在转化时，要用思维自觉地监控和控制自己的解题行为，在挑选策略或思维受阻时用元认知提示语[2]提示：“这个思考方向能最终解决问题吗？”“沿着哪条思路能达到解题目标？”“要暂停，试试其他解题方向吗？”“离最终解决问题还有多远？”“重新阅读条件，是不是漏掉了哪个条件？”通过元认知提示语不断地调节思维的方向，最终到达目的地.

3.3 反思解题过程

摸索解题路径的过程是一笔宝贵的财富，反思思维过程能得到很多数学直觉和解题策略上的经验.一是总结不同条件组合下，不同图形之间最重要的联系纽带是什么，与之相关的定理有哪些.如例题是等腰三角形与圆的组合，等腰三角形三线合一的性质就是思维的切入点.二是证明一个结论往往有哪些解题路径，把这个证明过程存入经验储备库中，以后遇到类似的问题，就可以转化来解决.如例题是证明弧等，下次除了想到弦等推弧等，也会想到圆周角相等推弧等.三是反思思维受阻时的做法，总结最佳的处理方式，完善解题策略.如例题中想证明BE=DE受阻时，若要坚持这个方向，要再认真观察图形结构，看看能否将问题转化.实在无法解决时，不妨换一个方向思考，证明弧等除了先证明弦等外，还有没有其他方法.

发展逻辑推理能力，不仅需要八方联系的严密的知识结构，同时还需要浮想联翩和寻找正确路径的解题策略.在“知”与“行”中不断感悟，方能造就强大的逻辑推理能力.

参考文献

[1]陳永明.数学习题教学研究[M].上海：上海教育出版社，2014：33-37.

[2]涂荣豹.数学教学设计原理的构建——教学生学会思考[M].北京：科学出版社，2018：60-62.