基于确定性下的尺规作图

1 试题呈现

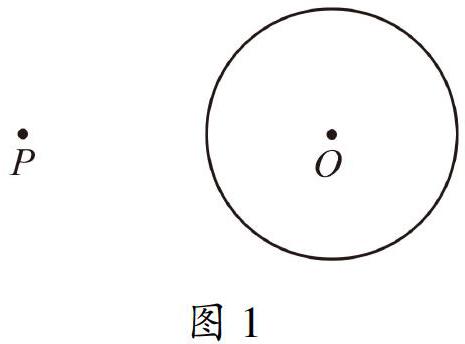
（2021南京）如图1，已知P是⊙O外一点.用两种不同的方法过点P作⊙O的一条切线.要求：（1）用直尺和圆规作图;（2）保留作图的痕迹，写出必要的文字说明.

2 试题探究

对于这样一道熟悉的问题，也是课堂教学的真实情境再现，学生通过初中三年的几何学习，将一些基本的几何模型通过本题较好的呈现，体现了试题的评价功能，将学生熟悉的素材以发散性的形式进行考查，体现了思维的多样性.本题的素材也是源于新版《义务教育课程标准》中的案例，为教学提供了新的导向.下面我们将从理解题意、拟定方案、执行方案、回顾反思对试题进行探究.

2.1 理解题意

分析题目的条件，⊙O是定圆，点P是⊙O外一定点，需要在⊙O上寻找一个定点Q，使得PQ是切线，即∠PQO=90°.

2.2 拟定方案

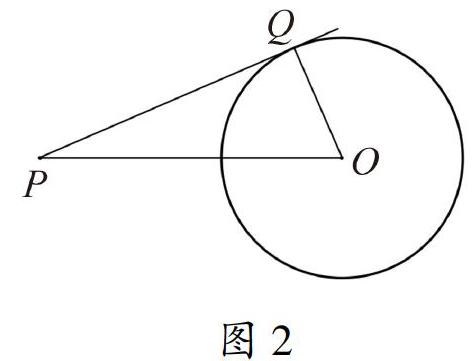
我们通过构造示意图，如图2，观察∠PQO=90°，对于这个直角模型你能联想到什么？如何构造相应的几何模型来实现∠PQO=90°？

联想1（定弦定角） 由于PO是定线段，∠PQO=90°，它们都是确定元素，因此点Q的轨迹是圆弧.定弦定角的数学模型学生非常熟悉，很容易联想到轨迹，因此以PO为直径构造圆，与⊙O的交点即为所求，从而确定切线.联想2（HL全等） 由于PO长度固定，半径OQ已知，∠PQO=90°，因此Rt△POQ是确定的，基于三角形确定的情形下，我们可以利用尺规作图构造出这个直角三角形，其实这就是判定两个直角三角形全等的条件“HL”.通过截取直角边，进一步得到切线长.上述两个作法对于学生是容易得到的，教学中，我们希望学生能够发散思维，在想到2个解法之后能再想一步，还可以怎么做？又是如何想到的？

联想3（三线合一） 从直角三角形可以联想到等腰三角形，根据等腰三角形的“三线合一”再得到直角三角形.转化思维，不妨在原图形的基础上构造一个更大的图形来实现本题最初的想法.线段PO是等腰三角形的腰，OQ是这个等腰三角形底的一半，故等腰三角形确定，因此图形如何构造就豁然开朗.基于联想3的再思考，我们可以从等腰三角形构造这个直角，也可以借助菱形的对角线互相垂直来实现这个构图的想法，此时的图形就“更大”了.

联想4（特殊位似） 根据联想3，从图形的大小启示我们，间接构图，从位似的视角来构造直角三角形.特别地，利用中位线构造图形更加容易，此刻的三角形是确定大小和形状.

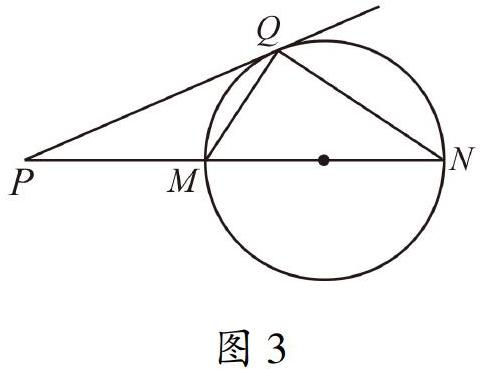
联想5（一般相似） 根据联想4相似的视角，利用切线和割线构成的三角形相似，如图3，得到PQ2=PM·PN.因为PM与PN长度确定，因此切线长PQ确定.基于这样的比例式，多视角认识相似，那么构图的方法就比较丰富了.

联想6（垂径定理） 借助圆的垂径定理进行构图，垂径定理可以得到垂直，再结合圆的相关知识进行解答.联想7（三高相交） 图2的构图让我们联想到OQ是△POQ的高，根据三角形的“三条高所在直线交于一点”的结论，如果能够构造出一个三角形的另外两条高，那么OQ⊥PQ就自然生成.如何构造三角形？怎样构造会容易想到？借助“三条高所在直线交于一点”的结论，不断尝试画图，这种逆向的思考会让更多的学生感悟到数学的奇妙.

2.3 执行方案

方法一 根据联想1作图，如图4，以OP为直径构造⊙M，⊙M与⊙O的交点为Q，PQ即为所求.类似的，我们也可以截取MQ=MO=MP，从而得到∠PQO=90°实现作图.

方法二 根据联想2作图，如图5，以Q′为直角顶点构造∠O′Q′P′=90°，截取O′Q′=r，截取线段O′P′=OP，根据全等三角形的性质可得线段P′Q′=PQ.以P为圆心，P′Q′长为半径作弧交⊙O于点Q，PQ即为所求.类似的，如图6，构造PQ=AB，PQ即为所求.

方法三 根据联想3作图，如图7，以P为圆心，PO长为半径作弧，以O为圆心，2r长为半径作弧，两弧交点为A，连接AO.AO交⊙O于点Q，PQ即为所求.类似的，如图8，构造菱形实现作图.

方法四 根据联想4作图，如图9，延长PO至点A，使得PO=OA，以O为圆心，PO长为半径作弧，以A为圆心，2r长为半径作弧，两弧交点为D，连接PD，PD与⊙O交于点Q，PQ即为所求.类似的，如图10.

方法五 根据联想5作图，如图11，以PC为直径作⊙A，PC与⊙O交于B，过点B作DB垂直于PC，交⊙A于点D，连接PD，以P为圆心，线段PD长为半径作弧，交⊙O于点Q，线段PQ即为所求.类似的，我们扩大图形，如图12，延长BP至点A′，使得A′P=AP，同理可得切线PQ.

如图13，在⊙O上任取一点A，连接PA，过A作∠OAB=∠OPA，易得OA2=OB·OP，

过点B作BQ⊥OP，交⊙O于点Q，因此OQ2=OB·OP，所以∠PQO=90°，则可得切线PQ.

如图14，在⊙O上任取点B，连接PB，交⊙O于另一点A，过C作∠OCD=∠BPO，交OB于点D，易得OB2=OD·OP，在OP上取点E使得OE=OD.过点E作EQ⊥OP，交⊙O于点Q，因此OQ2=OE·OP，所以∠PQO=90°，则可得切线PQ.

進一步的改造上述方法，如图15，构造∠PAC=∠POB，交PO于点C，过点C作CQ⊥OP，交⊙O于点Q，因此∠PQO=90°，则可得切线PQ.

如图16，在上述的方法中，由于垂足点是确定位置的，因此可以尝试连线形成交点从而确定切点弦，此法的最大优势是只用直尺进行作图.

方法六 根据联想6作图，如图17，以O为圆心，OP为半径构造大⊙O，任意取小圆半径OA，

过点A作CD⊥OA，分别交大⊙O于C，D两点.以P为圆心，CD为半径构造⊙P，⊙P与大⊙O交于E点，连接PE交小⊙O于点Q.则可得切线PQ.

如图18，任意作线段PB，交⊙O于C，B两点.过点O作OA⊥PB，垂足为点A，以A为圆心，AP为半径构造⊙A.过点B作BE⊥PB，交⊙A于E，以P为圆心，BE为半径作弧，交⊙O于点Q，则可得切线PQ.

方法七 根据联想7作图，如图19，20，我们先看看思维的过程.

图21从图19到图20的演变中，我们能感受到三高所在直线交于一点的巧妙，那么垂直相切就显而易见.如图21，延长PO交⊙O于点B，过点B作直线l垂直于PB，垂足为B.在l上找一点C，使得OC=PO，作PC的垂直平分线交l于点E，连接PE交⊙O于点Q，则可得切线PQ.

2.4 回顾反思

2.4.1 关注模型思想

对于本试题，我们从多个角度建立直角模型，从而构建出初中数学中基本的几何模型.联想1从定线段、定角这个角度思考，构建定弦定角的数学模型.联想2从三角形确定性角度思考，以全等为抓手，构建直角三角形.联想3关注转化的思想，将确定的直角三角形转化成为等腰三角形截取得到，换个角度看问题，这边风景独好.联想4从特殊的位似思考，或者说利用中位线来解决问题，熟悉的背景，不一样的感悟.联想5的多种相似构造，彰显几何内功，从一些结论出发倒推相似得直角，将几何模型运用的炉火纯青.联想6关注圆中的垂径定理的灵活使用，让方法更加多元，将相似与圆的多个结论融合在一起.联想7从学生熟悉而又陌生的“三高交于一点”展开思考，熟悉是因为小学画图时就知道此结论，陌生是学生不一定会构图，作图的魅力是从念头开始，不断尝试和思考构造模型，证明不言而喻.

从拟定方案到执行方案，我们不是一味的追求多解和巧解，而是希望这个“直角”能够带给学生多角度的思考和深层次的再思考，用一道试题构建几何学习的整体框架，加深对每一个知识点的理解，从而加强模型思想的渗透.

2.4.2 关注课堂教学

这道试题在教师新授课或者复习课時都会有所涉及，属于一道“老题”，但老题背后却反应的是教师的教和学生的学.教师在课堂教学时要关注通性通法的讲解，要舍得花时间让学生去体验，去思考，去书写，去交流，去质疑等环节，要关注到学生之间的差异，从而体现到方法上的差异，进一步呈现出思维上的差异，教师要及时给予鼓励和引导，让学生成为学习的探究者.学生在课堂学习时要主动参与，独立思考，敢于尝试，学会聆听教师和同伴的讲解，当遇到多种方法解题时，掌握通性通法，接受并学习不一样的方法，同时关注不同方法之间存在差异的原因，学会反思，学会交流和学会创新.

2.4.3 关注考试评价

南京中考试题近年来关注两种方法的解答，这在全国都不是很多见，而两种方法背后承载着教师和学生对于数学的理解，呈现的是学生对于不同数学模型的理解和应用，具有较好的选拔功能.两种方法的考查也指引着课堂教学的变革，课堂不是教师的一言堂，要让更多的孩子参与到课堂来，鼓励因材施教和分层教学.例如本试题的教学，教师要放手给学生在课堂中尝试并探究各种作法，引导学生交流和互相评价，关注学生的原始生成，适时引导和帮助，让不同的孩子在数学上有不同的发展.另外，试题中出现了“保留作图的痕迹，写出必要的文字说明”，说明在评价中关注到了用数学的语言去表达作图的想法，同时也倒逼作法的精准性，加强学生对于问题的理解.

正如波利亚所言：没有一道试题可以解决的十全十美.希望同学们能够将“理解题意，拟定计划，执行计划，回顾反思”的解题四步法深入内心，从确定性的角度思考问题，这样的问题解决才会更让人心动.

作者简介 王强（1987—），男，江苏南京人，硕士，伊犁州优秀援疆教师，伊宁市优秀教师，南京市优秀青年教师，南京市秦淮区数学学科带头人.