魅力无穷的赵爽“弦图”

高顺华

[真题呈现]

例1（2020·湖南·娄底）由4个直角边长分别为a，b的直角三角形围成的赵爽“弦图”如图1所示，该图根据大正方形的面积c2等于小正方形的面积（a - b）2与4个直角三角形的面积2ab的和证明了勾股定理a2 + b2 = c2，还可以用来证明结论：若a > 0，b > 0且a2 + b2为定值，则当a b时，ab取得最大值.

[追根溯源]

例2（八年级上册第5页“做一做”）为了计算图2中大正方形的面积，小明对这个大正方形适当割补后得到图3和图4.（1）将所有三角形和正方形的面积用a，b，c的关系式表示出来;（2）图3、图4中正方形ABCD的面积分别是多少？你们有哪些表示方式？与同伴交流.（3）你能分别利用图3、图4验证勾股定理吗？（解答过程略）

[破解策略]

例1首先介绍了用赵爽“弦图”来证明勾股定理的思路，然后提出了新问题：若a > 0，b > 0且a2 + b2为定值，问当a，b之间有什么样的数量关系时，ab取得最大值.

由于a2 + b2为定值，我们不妨设a2 + b2为k，则c2 = a2 + b2 = k. 由赵爽“弦图”可知，2ab = c2 - （a - b）2 = k - （a - b）2，即ab = [k-（a-b）22]. 很明显，当a = b时，（a - b）2取最小值0，因此当a = b时，ab取得最大值，最大值为[k2]. 故应填“ = ”.

由上可见，对于最大（小）值的问题，我们常常将其转化为两个数差的平方，再借助于完全平方数的非负性来处理.这里是利用代数方法来解决几何问题，体现了数形结合的思想.

[原题延伸]

变式1：将赵爽“弦图”的四个直角三角形重新摆放

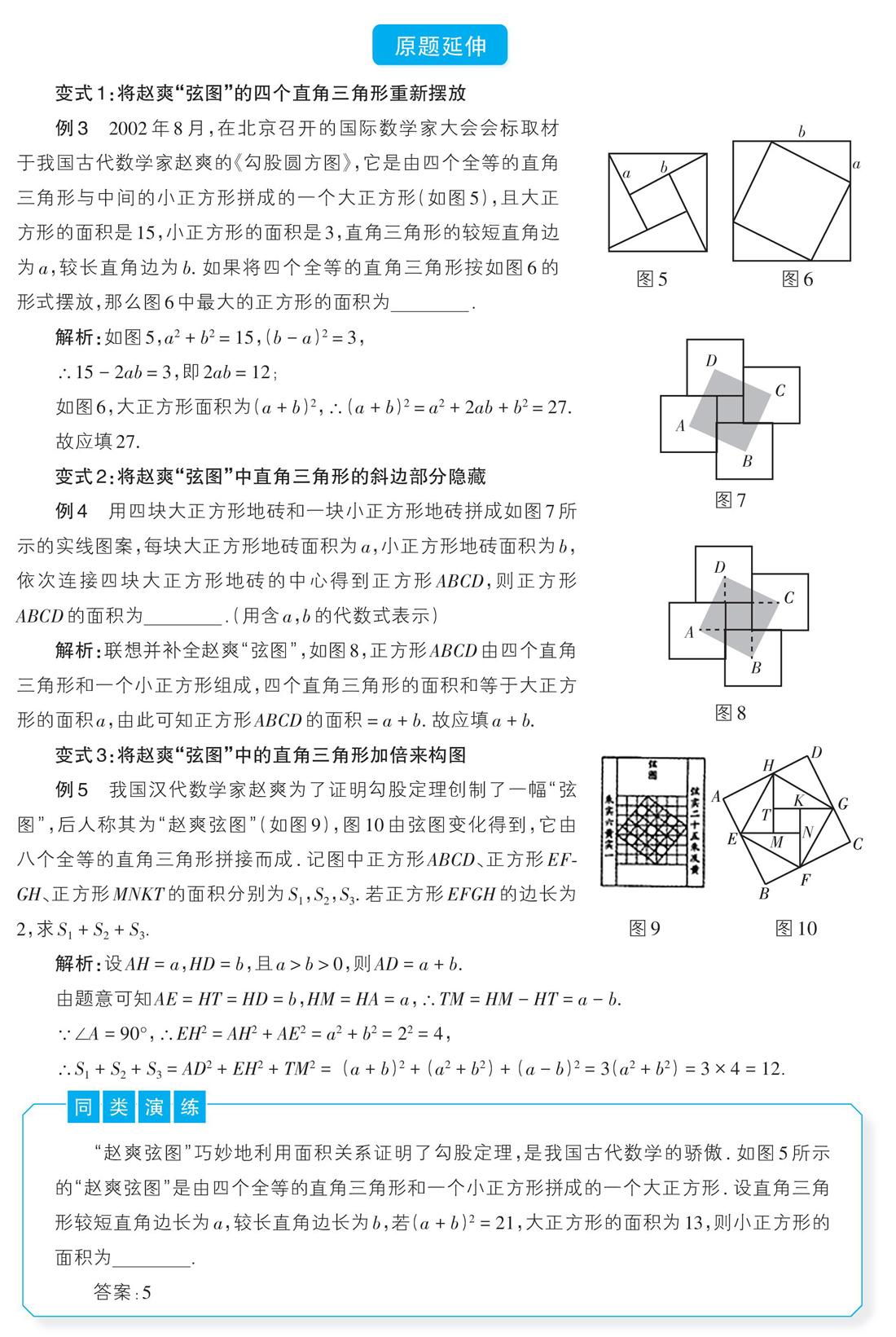
例3 2002年8月，在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形（如图5），且大正方形的面积是15，小正方形的面积是3，直角三角形的較短直角边为a，较长直角边为b. 如果将四个全等的直角三角形按如图6的形式摆放，那么图6中最大的正方形的面积为_________.

解析：如图5，a2 + b2=15，（b - a）2=3，

∴15 - 2ab=3，即2ab=12;

如图6，大正方形面积为（a + b）2，∴（a + b）2=a2 + 2ab + b2=27.

故应填27.

变式2：将赵爽“弦图”中直角三角形的斜边部分隐藏

例4 用四块大正方形地砖和一块小正方形地砖拼成如图7所示的实线图案，每块大正方形地砖面积为a，小正方形地砖面积为b，依次连接四块大正方形地砖的中心得到正方形ABCD，则正方形ABCD的面积为_________.（用含a，b的代数式表示）

解析：联想并补全赵爽“弦图”，如图8，正方形ABCD由四个直角三角形和一个小正方形组成，四个直角三角形的面积和等于大正方形的面积a，由此可知正方形ABCD的面积=a + b. 故应填a + b.

变式3：将赵爽“弦图”中的直角三角形加倍来构图

例5 我国汉代数学家赵爽为了证明勾股定理创制了一幅“弦图”，后人称其为“赵爽弦图”（如图9），图10由弦图变化得到，它由八个全等的直角三角形拼接而成. 记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1，S2，S3. 若正方形EFGH的边长为2，求S1 + S2 + S3.

解析：设AH = a，HD = b，且a>b>0，则AD = a + b.

由题意可知AE = HT = HD = b，HM = HA = a，∴TM = HM - HT = a - b.

∵∠A = 90°，∴EH2 = AH2 + AE2 = a2 + b2 = 22 = 4，

∴S1 + S2 + S3 = AD2 + EH2 + TM2 =  （a + b）2 + （a2 + b2） + （a - b）2 = 3（a2 + b2） = 3 × 4 = 12.

同类演练

“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲. 如图5所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形. 设直角三角形较短直角边长为a，较长直角边长为b，若（a + b）2 = 21，大正方形的面积为13，则小正方形的面积为_________.

答案：5