不确定结构时域响应分析的多项式维数分解法
赵 岩, 刘 凡, 孙晓旭
(大连理工大学 工业装备结构分析国家重点实验室 工程力学系,大连 116024)
1 引 言
不确定性因素广泛存在于各工程领域,通常应用的确定性模型只是实际结构的一种近似模型化方式,以确定性分析严格作为结构设计标准将会带来一定的风险。采用随机结构模型是实际结构更为合理的模型化方法,目前,考虑不确定性因素在结构中的传播及合理度量不确定性因素对结构响应的影响已经成为动力学研究的重要课题[1-3]。
在关于不确定性分析的研究工作中,最早应用的摄动技术是比较流行的方法,在实际应用中通常采用二阶截断展开,对于更高阶情形的求解将会变得非常复杂。此外,摄动法一般只适用于小尺度变异的随机问题,成为其固有的缺陷[4]。吴锋等[5]提出了快速摄动法,较好地解决了摄动法的复杂展开计算问题。蒙特卡洛方法MC(Monte Carlo method)是处理不确定动力学问题的另一种有效方法,其基于样本分析的策略能够有效应用于线性和非线性问题等各研究领域[6,7];其较为明显的不足之处在于收敛效率问题,为了得到可靠的计算结果,需要较高的样本数量[4]。目前,针对小样本的MC方法成为研究的一个主要方向[8,9]。
对于不确定结构动力学,谱随机方法植根于概率和测度空间的丰富数学基础之中,近年来成为处理不确定问题的重要手段。Cameron-Martin定理指出,在L2空间中任意二阶随机过程可以由正交多项式序列予以均方逼近,成为谱随机方法的核心出发点。基于多项式逼近的Galerkin映射方法成功应用于动力学问题分析。由于需要求解的方程组规模远大于原始随机问题,当涉及随机因素较多时,矩阵维度会显著增加,该方法只能用于简单的分析模型[10,11]。维数分解法[12,13]采用一组变量维数逐次增加的成员函数对原高维随机函数进行分解,是一种有限、分层且收敛的展开,实现了降维目的。之后,Rahman将成员函数进行Fourier展开,提出了多项式维数分解法,即PDD(Polynomial dimensional decomposition)方法[14]。该方法给出了原随机函数关于随机变量的简单映射关系,能够根据展开系数快速求得原随机函数的统计矩,已广泛应用于灵敏度分析[15]、不确定性设计[16]和随机动力系统频域稳态分析[17]等,显示出良好的应用前景。
本文将上述PDD方法推广用于不确定结构的时域响应分析,采用参数概率模型来描述不确定性,建立随机结构动力学方程。将结构不确定时域响应表达为不确定参数的函数,进一步将关心的不确定时域响应进行维数分解,并利用正交多项式进行Fourier展开。采用降维积分方法进行展开系数的计算,并最终进行不确定结构响应统计量随时间演变过程的分析。数值算例中,通过具有解析解的不确定单自由度动力响应分析验证所提出方法的正确性,进而采用具有不确定参数的多自由度桁架结构进行了方法的一般性应用,并同MC方法进行对比,验证所建立方法的有效性。
2 具有不确定参数结构的运动方程
在实际的工程结构中,由于不确定的材料物理参数和不可避免的加工制造误差等广泛存在的不确定性,使得结构的刚度和质量等参数也具有不确定性。假定结构中所有的不确定参数均为服从特定概率密度分布的独立随机变量,并假定外荷载与结构的不确定参数相互独立。此时,具有不确定参数结构在外荷载作用下的运动方程可表示为
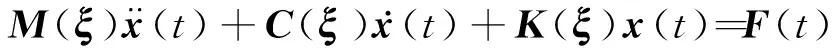
(1)
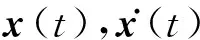
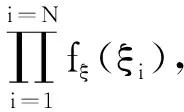
x(t,ξ)=G(t,ξ1,ξ2,…,ξN)
(2)
由于结构中存在不确定参数,使得结构的时域响应向量x(t,ξ)的每一个元素在任意时间t处都是关于不确定参数ξ的函数。对于大型复杂结构而言,往往只关心结构部分节点的响应,假设x(t,ξ)是x(t,ξ)的某一个观测自由度,将其表示为关于ξ的函数
x(t,ξ)=g(t,ξ1,ξ2,…,ξN)
(3)
本文利用PDD方法对式(3)的结构响应函数在每个时间步处进行维数分解和Fourier展开,进一步利用展开系数计算得到结构响应的均值和标准差。
3 时域响应分析的PDD方法
3.1 多项式维数分解法
将结构时域响应x(t,ξ)进行维数分解并取P元近似,可表示为[14]
(4)
式(4)可视为对多元随机函数x(t,ξ),采用一组变量维数逐次增加的成员函数进行分层近似,且这种分层近似在每一时间步t内进行。在式(4)中
(5)
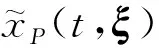
将式(4)的成员函数进行Fourier展开,并取前m阶截断,将其表示为展开系数与正交多项式基底的乘积形式
(6)
式中P取1,2,3时分别对应一元、二元和三元展开系数。式(6)的展开系数可按式(7)计算
(7)
式中Ψj(ξi)表示第i个随机变量ξi的第j阶正交多项式基底,关于展开系数和正交多项式基底的内容可参见文献[14]。利用式(6)的Fourier展开后,可将原来没有显示映射关系的成员函数近似表达为简单的函数映射关系,再根据式(4),便能够得到结构响应函数x(t,ξ)的显式函数映射关系。
在对结构时域响应进行维数分解和Fourier展开后,响应的均值和方差可按式(8,9)计算[18]。
E[x(t,ξ)]=x0(t)
(8)
(9)
相应地,可由式(9)得到结构时域响应标准差SD(Standard deviation)的计算公式。
3.2 降维积分方法
在计算式(5)的x0(t)和式(7)的Ci1…iPj1…jP(t)时,需要进行N维积分,当随机变量维数较大时,计算成本高昂,对此本文采用降维积分方法[14]。令c={c1,c2,…,cN}T为随机变量ξ的均值,将x(t,ξ)的N-(R-q)个随机变量用c相对应的均值代替,得到x(t,ξ)的R-q阶近似为
xR -q(t,ξ)=x(t,c1,c2,…,cq1-1,ξq1,cq1+1,…,
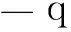
(10)
此处,P≤R≤N(q=0,1,…,R)。如当R=1时,0维分量函数(对应q=1)对于给定的时间t是一个常量x(t,c),一维分量函数(对应q=0)对于给定的时间t是N个一元函数x(t,ξ1,c2,…,cN),x(t,c1,ξ2,c3,…,cN),…,x(t,c1,c2,…,cN -1,ξN)。定义函数x(t,ξ)的R元近似
(11)
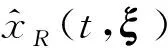
3.3 计算量分析
4 数值算例
给出2个数值算例,分别为具有不确定参数的单自由度系统和10杆桁架结构,用于验证本文提出的PDD方法的精确性和计算效率。在单自由度系统算例中,系统仅含有1个不确定参数,主要用于研究PDD方法中多项式基底数目对标准差计算精度的影响。在10杆桁架算例中,结构中存在12个不确定参数,主要用于研究不同R值对均值的影响,以及研究不同R,P和m值对标准差计算精度的影响。算例1中,解析解和MC模拟结果将作为PDD方法计算结果的参照。算例2中,MC模拟结果将作为PDD方法计算结果的参照。
4.1 单自由度系统
单自由度无阻尼系统的自由振动方程可表示为[1]
(12)
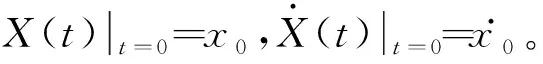
分别采用MC和PDD两种方法计算系统位移响应的均值和标准差,分析时间为0 s~15 s,时间步长取0.01 s。MC方法的样本数量取105,PDD方法中多项式基底数目取12,采用解析积分计算均值和展开系数。根据文献[1]给出的系统位移响应均值以及标准差的解析表达式计算得到的结果,作为本文PDD方法的参照。
图1给出了分别由PDD方法和MC方法计算得到的系统位移响应均值曲线,可以看出,PDD方法计算得到的系统位移响应均值与解析解及MC模拟结果吻合良好。实际上,在该算例中只有一个随机变量,由PDD方法的展开系数计算式(5)可知,当采用解析积分时,PDD方法计算得到的均值与解析解是完全一致的。值得注意的是,对于算例中的随机系统,其响应的均值呈现出衰减的趋势,当时间t→∞时,响应的均值为0。无阻尼确定参数系统的响应不会随时间衰减,这表明确定系统响应和不确定系统响应有显著不同[1]。
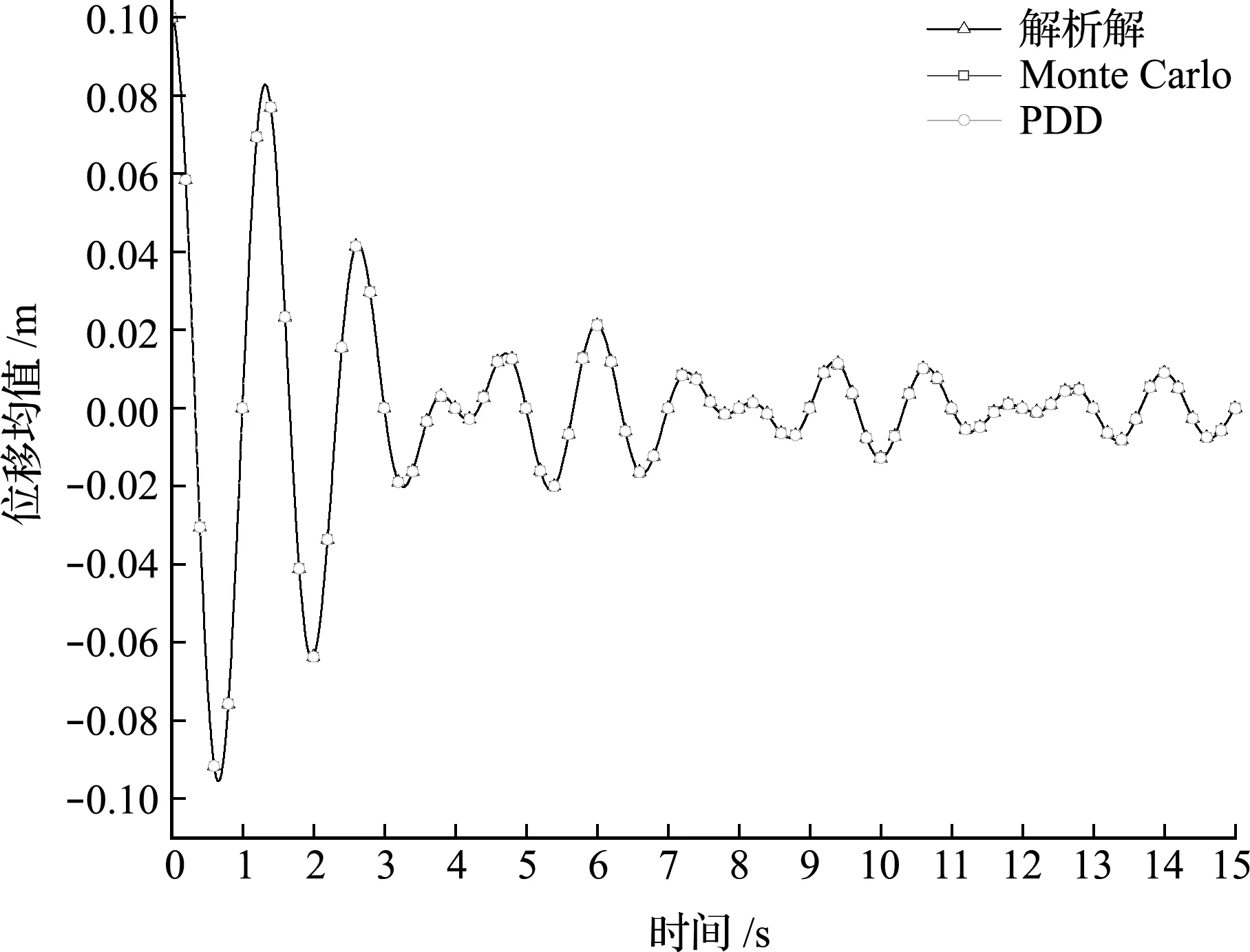
图1 位移响应均值
图2给出了PDD方法和MC方法计算得到的系统位移响应标准差。可以看出,当基底数目很少时,PDD方法计算得到的标准差在初始的一段时间里能够和MC模拟结果以及解析解相吻合,但随着时间的增大,吻合程度逐渐变差。当增加基底数目时,PDD方法计算得到的标准差在更长的一段时间内与MC模拟结果及解析解相吻合。由此可知,在PDD方法中可以通过增加基底数目以获取更加精确的计算结果。由系统响应均值和二阶原点矩的解析表达式可知,当t→∞时,响应方差会逐渐收敛于稳定值,因此可以只计算相对足够长的一段时间内的标准差即可。在此算例中,PDD方法取合适的基底数目(如m=12)便足够,不需要取无穷多项。
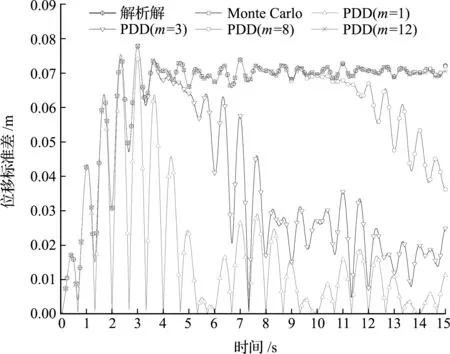
图2 位移响应标准差
4.2 10杆桁架
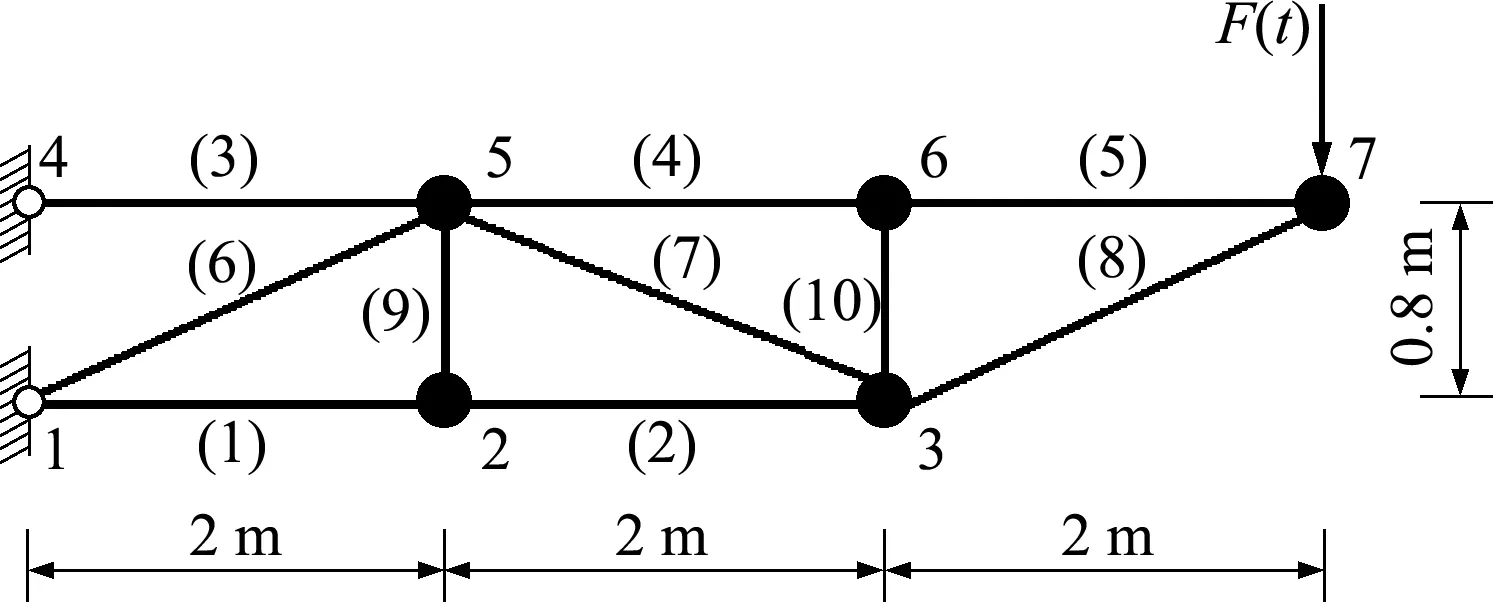
图3 10杆桁架

表1 桁架随机变量参数
图4给出了采用PDD方法和MC方法计算得到的杆3轴向应力均值。可以看出,PDD方法计算得到的结构响应均值曲线与MC方法结果吻合良好,即使取R=1,也能得到与MC方法相吻合的结果,这表明PDD方法具有足够的精确性。
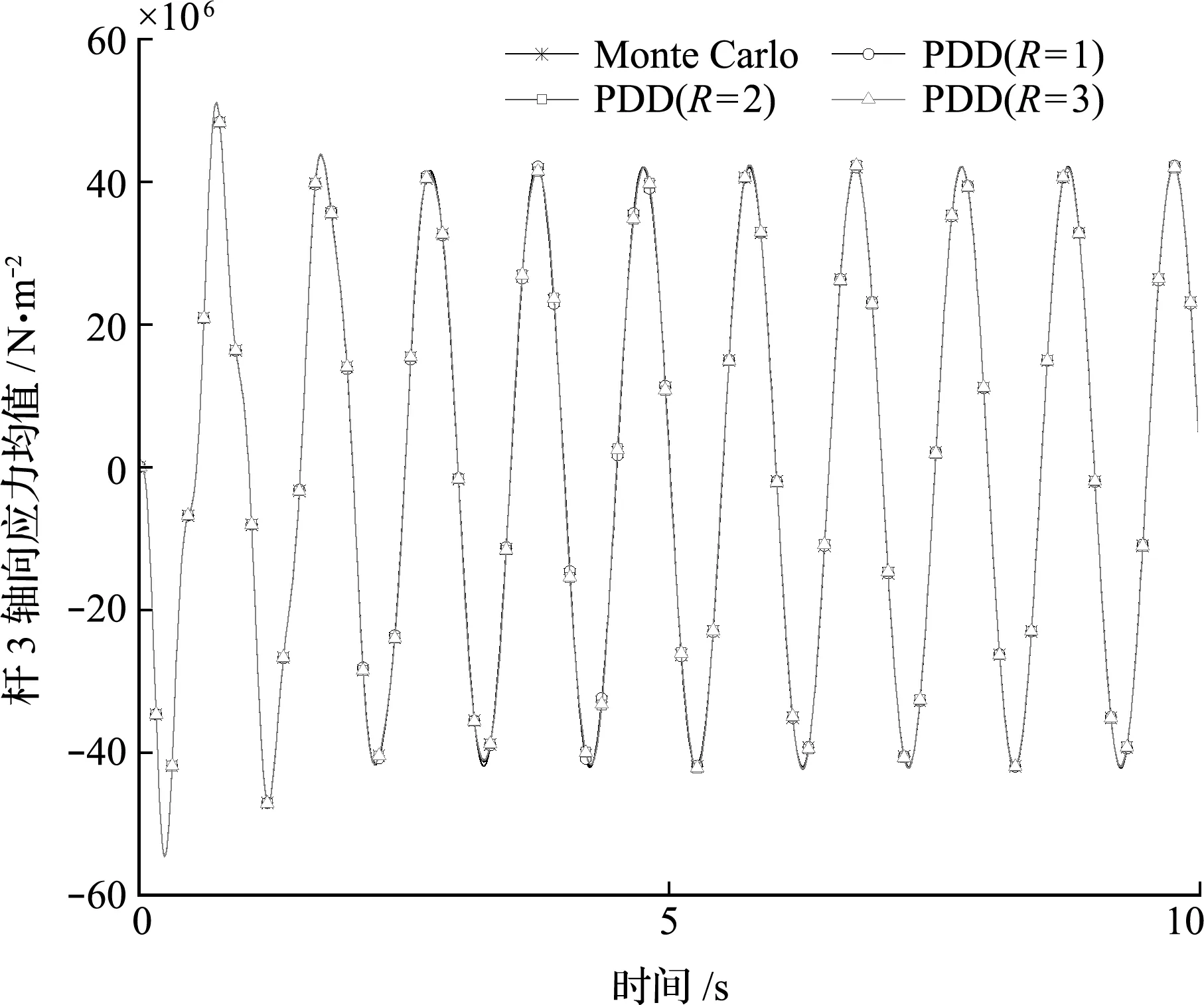
图4 杆3轴向应力均值
图5给出了PDD方法和MC方法计算得到的结构响应标准差。在PDD方法中,P分别取1,2和3用于对比不同P值对结构响应标准差的影响。可以看出,当P=1时,PDD方法计算得到的响应曲线与MC方法模拟结果稍有偏差,但随着P的增大,PDD方法计算结果与MC方法结果吻合程度更好,表明在PDD方法中可以通过增大P的取值来提高计算精度。
图6和图7分别给出了PDD方法在不同R和P值(R=P)以及不同多项式基底数目m时,计算得到的结构响应标准差与MC方法模拟结果的对比曲线。可以看出,在PDD方法中,增大R,P或m的值均能够提高计算精度。在该算例中,取R=P=2时便能够得到与MC方法非常吻合的计算结果。
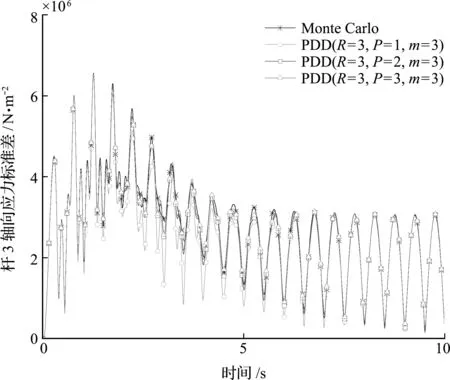
图5 不同P值时的杆3轴向应力标准差
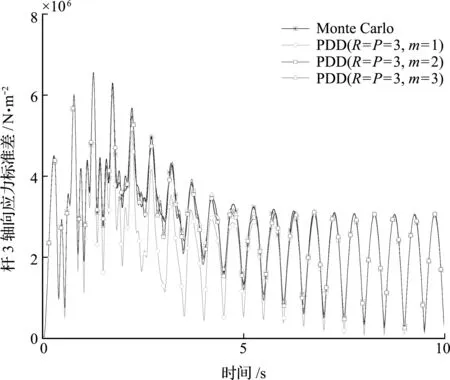
图6 不同m值时的杆3轴向应力标准差
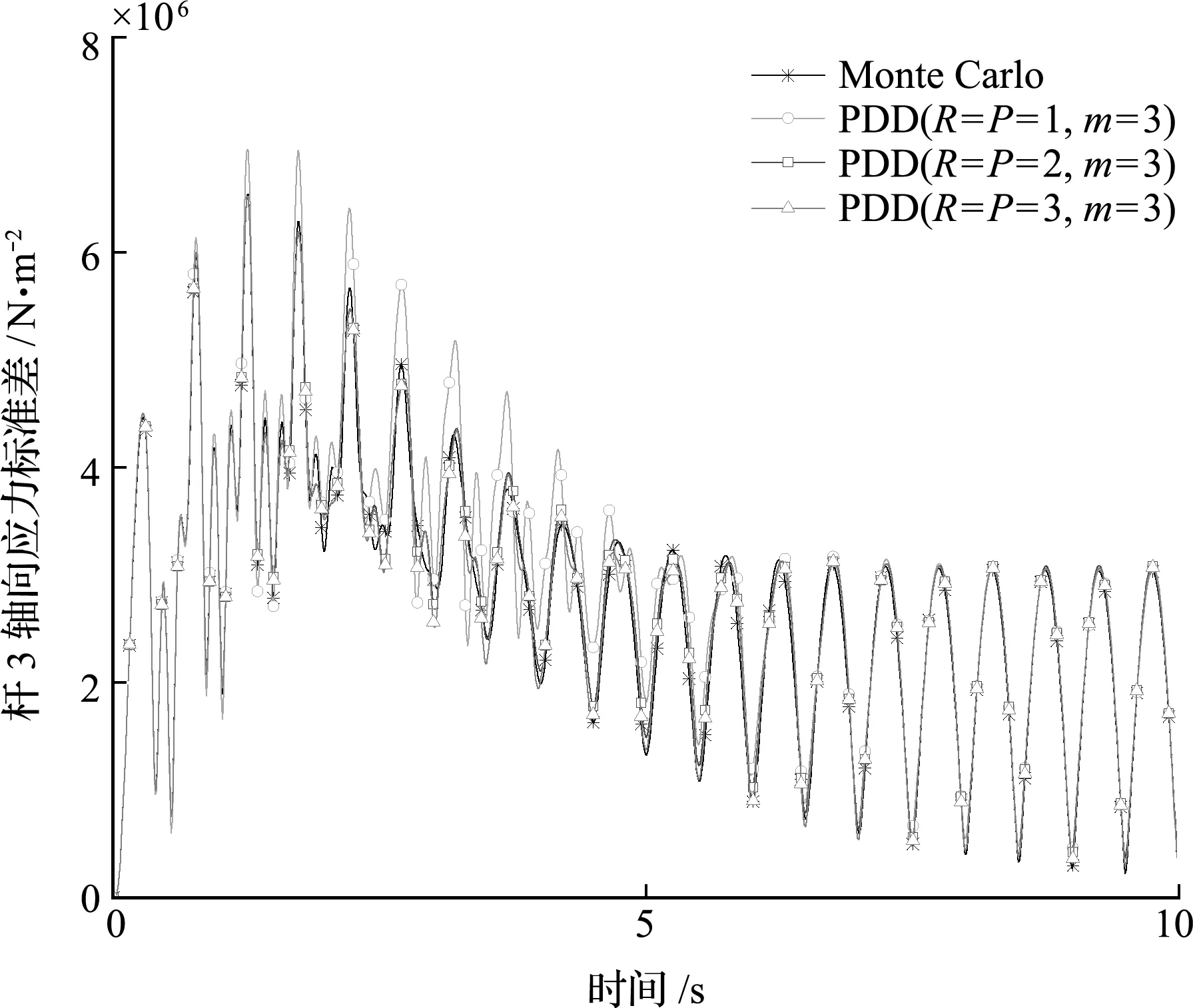
图7 不同R值和P值时的杆3轴向应力标准差
表2给出了PDD方法与MC方法所需的时域响应分析次数,由表中数据可知,PDD方法所需时域响应分析次数远少于MC方法。虽然本文给出了R=P=3的PDD方法计算结果,但实际上取R=P=2时便有与MC方法相当的精度,而PDD方法所需的时域分析次数仅为289次,不到MC方法所需次数的3%,采用PDD方法可节省大量的分析时间。对比PDD方法不同R和P值时的分析次数可知,随着降维积分变量数目的增加,动力学响应分析所需的次数也会增加,在应用PDD方法时,可以使P与R取相同的值,这样既能提高精度,且不会增加额外的计算量。

表2 时域响应分析次数
PDD方法中,在每个积分节点处进行的时域响应计算与确定参数结构的时域响应计算的基本原理是一致的,其计算精度和效率依赖于选取的时域积分方法和积分时间步长。常用的时域积分方法如Newmark法和精细积分法等在PDD方法中均能适用。
5 结 论
本文针对具有不确定参数结构时域响应求解问题提出了PDD方法。首先将结构时域响应表达为关于结构不确定参数的函数,然后采用一组变量数目逐次增加的成员函数对结构响应函数进行维数分解,并对成员函数进行Fourier展开,利用正交多项式基底给出成员函数的近似表达,并给出了由展开系数计算结构响应均值和标准差的表达式。提出的方法将复杂且非显式的函数映射关系表达为显式的函数映射关系。此外,该方法利用了降维积分法,将原来的高维问题转化为更低维度的问题,适用于多维和高维问题的分析。数值算例结果表明,提出的方法具有足够的精确性,且比MC方法更加高效,为具有不确定参数复杂结构动力学响应分析提供了一种准确和有效的求解方法。

