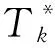复杂网络中k-单圈图的若干性质

姚 明，苏 静，姚 兵

(1.兰州石化职业技术学院信息处理与控制工程学院，甘肃 兰州 730060；2.北京大学信息科学技术学院，北京 100871；3.北京大学高可信软件技术教育部重点实验室，北京 100871；4.西北师范大学数学与统计学院，甘肃 兰州 730070)

1 预备知识

在当今的网络世界里，无标度网络几乎处处可见，如演员网络、语言网络、万维网等[1].Genio等[2]已经证明所有无标度网络都是稀疏的.因此，通过构造方法可以得到对于任意实数M>0，存在一个无标度图N(t)和一个数β≥M，使得|E(N(t))|～β·|N(t)|.本文研究k-单圈图变量的动机来自许多仍待解决的猜想[3]，图的许多来自Graffiti猜想[4]的不变量，以及实际应用中需要大量的优质网络模型.

设k为非负整数，G是连通图.如果G中恰好包含k个圈，且这k个圈的任何两个圈之间没有公共边，那么称图G为k-单圈图.特别地，树是0-单圈图.k-单圈图也叫仙人掌图，仙人掌图的每个块是一个圈或是一条路，或者说，仙人掌图的每条边都包含在至多一个圈中.如果k-单圈图G含有不在圈上的边，则G不是欧拉图.

本文考虑没有自环和重边的有限无向图.文中未定义的术语均来自文献[5].对整数n>m≥0，约定[m，n]={m，m+1，…，n}.在图G中与顶点u相邻的点的集合记为N(u)，因此，顶点u的度数degG(u)等于基数|N(u)|.称N(u)和N[u]=N(u)∪{u}分别为顶点u的邻集和闭邻集.类似地，一个顶点子集S⊂V(G)的邻集N(S)是集合V(G)的子集，使得每一个x∈N(S)顶点都与S中的一个顶点相邻.度数为1的顶点称为叶子.符号L(G)表示图G的叶子集，nd(G)表示G中度为d的顶点的数目.特别地，nd(G)=0表示G是一个孤立点或者G中没有度为d的顶点.

设P=u1u2…um是图G的一条路.若degG(u1)≥3，degG(um)≥3，且degG(ui)=2(i∈[2，m-1])，则称P是一条纯路.若degG(u1)≥3，degG(um)=1，且degG(ui)=2(i∈[2，m-1])，则P被称为悬挂路.类似地，如果一个圈G中的|V(C)|-1个顶点在图G中的度均为2，则称它为悬挂圈.本文将用到以下三类连通图的2个引理：

图1 三类连通图

上式指明，树中每一个2度顶点与树的叶子数量无关.

引理2[6-7]设T是一棵n个顶点的树，则Diam(T)≤n-n1(T)+1.

定理1 设G是一个含有p个点q条边的连通图，其中p≥3，q≥2.那么

(1)

证明如果连通图G是树，则它满足引理1中的公式，且q=p-1，可得到公式(1).设连通图G含圈，取它的某个圈上的一条边u1u2，给连通图G添加2个新顶点v1，v2，将顶点vi分别与顶点ui(i=1，2)用边连接，然后删去边u1u2，得到的图记为G1，得到图G1的过程称为减圈运算.不难看到，图G1是连通的，它的圈数目比图G的圈数目少1，且有

n1(G1)=n1(G)+2，nd(G1)=nd(G)(d≥3)，

|V(G1)|=p+2，|E(G1)|=q+1.

若图G1仍然含有圈，进行上述减圈运算，得到连通图G2，使得

n1(G2)=n1(G1)+2=n1(G)+4，nd(G2)=nd(G)(d≥3)，

|V(G2)|=|V(G1)|+2=p+4，|E(G2)|=|E(G1)|+1=q+2.

如此进行下去，直到连通图Gk不再含有圈，即它是树.注意到

n1(Gk)=n1(G)+2k，nd(Gk)=nd(G)(d≥3)，

|V(Gk)|=p+2k，|E(Gk)|=q+k.

根据引理1的公式得

进一步，有

由于q=p-1+k，结论得证.

根据平面图的欧拉公式和定理1的公式(1)，可得下面推论：

推论1 设φ(H)是连通平面图H的面数，则H满足

(2)

2 主要结论及其证明

k-单圈连通图G的点路圈图H为顶点集V(H)中的每一个顶点对应G中的一个圈，或者一条悬挂路，或者一条纯路，或一个大割点u(割点u使得不连通图G-u至少包含3个分支).2个顶点X，Y∈V(H)在点路圈图H中是相邻的，如果它们对应的圈X=Cm，Y=Ct(或者路X=Pm，Y=Pt，或一个圈X=Cm和一条路Y=Pt，或一个割点X=u和一个圈Y=Cm，或一个割点X=u和一条路Y=Pt)在G中总有|V(X)∩V(Y)|=1.图2给出连通图Gi的点路圈图Hi(i=1，2，3).

图2 连通图Gi的点路圈图Hi(i=1，2，3)

定理2 设G是一个连通图，整数k≥0，则：

(ⅰ)G是k-单圈图的充分必要条件为

(3)

(ⅱ)G是k-单圈图，当且仅当它的点路圈图是一棵树.

证明(ⅰ) 令ni=ni(G)，i=1，2.假设G是一个k-单圈图，根据k-单圈图的定义，存在边uivi(i∈[1，k])，使得G-{uivi|i∈[1，k]}是一棵树.构造一棵树：给图G添加新的顶点xi，yi(i∈[1，k])，分别用边连接顶点xi与ui，连接顶点yi与vi；然后删除边uivi(i∈[1，k])，所得的图记为H.显然，H是一棵树，且有Δ(H)=Δ(G).注意到

|V(H)|=|V(G)|+2k，n1(H)=n1+2k，nd(H)=nd(G)，d∈[2，Δ(T)].

根据引理1，有

(4)

这意味着公式(3)成立.

假设G满足公式(3)，如果G是树，使得

因此，有2=2(1-k)≤0，矛盾.假设G包含m≥1个圈，用上面的方法可以构造一棵树，使得

因此，2(1-m)=2(1-k)，从而m=k.

根据公式(2)和(3)，得到下面的结论：

定理3 设G是一个含有n≥3个顶点的k-单圈图，φ(G)是图G的面数，则φ(G)=k+1.

定理4 设G是一个n≥4个顶点的连通k-单圈图.对d∈[δ(G)，Δ(G)]，nd=nd(G)，则有k=|E(G)|-n+1以及下列性质：

(ⅰ) 2|E(G)|≤3(n-1).

(ⅲ)n≤2(k-1)+2n1+n2.

(ⅳ) 若对d∈[2，s]有nd=0，s≥2，则

sn≤2(k-1)+(s+1)n1+ns+1.

(5)

证明(ⅰ) 因为G的生成树有n-1条边，则k=|E(G)|-n+1.三角形是最小的圈，从而有

3k≤|E(G)|=k+(n-1)，

解得

2k≤n-1，2|E(G)|=2(k+(n-1))≤3(n-1).

(ⅱ) 利用定理1证明中的减圈运算以及

由平面图的性质得

再根据公式(3)，有2(1-k)+(n-n1-n2)≤n1.结论(ⅲ)的界由圈或者圈的每个顶点都有叶子的k-单圈图而获得.

(ⅳ) 设对d∈[2，s](s≥2)，有nd=0.使用公式(3)，可以得到

S={(vi，mi，vi+1，1)|i∈[1，k-1]}，

将(s-3)个新顶点与S中的每个顶点连接起来，得到图H.显然，

其中d∈[2，s].从而，H是一个k-单圈图并且满足不等式(5).

(1) 若n1(G)=0和|V(H*)|=k成立，H*的每个叶子都至少贡献两个G中度为2的顶点，因而得n2(G)≥2n1(H*)+n2(H*).更精确地，因为n1(H*)≥2和n2(H*)≥k成立.则有n2(G)≥k+2.