一类具有收获项的双时滞May合作系统的Hopf分支

王月月，吕堂红，周林华

(长春理工大学数学与统计学院，吉林 长春 130022)

0 引言

合作是物种之间的基本关系之一，在过去的几十年里，学者们对于合作模型进行了广泛研究[1-5].1976年May首次提出两种群合作模型，分析发现如果不对模型系数加以限制，其解可能无界.为了克服解的无界情形，May进一步考虑了种群内部密度制约因素，提出修正模型.此后对于May合作系统的研究多基于修正模型，如Cui等[6]提出并研究了非自治的May合作模型，给出了保证系统存在唯一的全局吸引的正周期解的充分性条件；Wei等[7]提出并探讨了具有捕获项的May合作系统，分析了系统正平衡点的存在性和稳定性.

2014年，杨坤等[8]研究了如下形式的具有避难所的May合作系统：

(1)

其中：x1，x2代表两个种群的密度；r1，r2分别表示两种群的内禀增长率；c1，c2分别表示两种群的种内竞争强度；bi表示xi种群与另一种群的合作系数；00，ci>0，i=1，2.假定x1种群具有避难所，此时数量为mx1的x1种群躲入避难所，(1-m)x1数量的x1种群与x2种群进行合作.其研究结果表明具有避难所的种群x1的平衡密度会随着避难所的增大而增大，而没有避难所的种群x2的平衡密度则随着对方种群避难所的增加而降低.

在实际问题中，影响种群密度的因素有很多.一方面，为了控制对生物资源的过度开发人类采取了多种措施，如设立保护区、制定法律法规保证适度开采等，希望既可以维持种群的持续生存，又能使经济得到较好发展.另一方面，时滞效应几乎存在于每种生物关系中，对于系统的稳定性产生极大的影响.因此，本文在模型(1)的基础上，考虑人为开采与捕捞作用，分别引入收获项e1x1和e2x2，考虑种群x1具有成熟期和孕育期[9]分别引入时滞τ1和τ2，提出如下具有避难所和收获项的双时滞May合作系统：

(2)

其中：τ1表示x1种群的成熟期；τ2表示x1种群的孕育期；eixi表示xi种群的收获项，ei>0，i=1，2；其他参数意义同模型(1).对于May合作系统的研究，学者们很少考虑到模型(2)，对于此模型的动力学行为研究也不多见，而这正是本文关注的焦点.

1 正平衡点的存在性

考虑到种群的生物学意义，本节讨论系统(2)正平衡点E*的稳定性状况.

定理1 如果r1>e1且r2>e2，则系统(2)有唯一正平衡点

证明如果系统(2)存在平衡点，则应满足方程组

(3)

由(3)式中的第2个方程可得

(4)

将(4)式代入(3)式中的第1个方程，有

(5)

其中：

P1=(r2-e2)r1b1b2c1(1-m)+r2b2c2(1-m)[r1(1-m)+r1a1c1]；

P2=[r1(1-m)+r1a1c1](r2+r2a2c2)+(r2-e2)r1a2b1c1-
(r1-e1)(1-m)b2[(r2-e2)b1+r2a1c2]；

P3=(e1-r1)[(r2-e2)a2b1+a1(r2+r2a2c2)].

不难发现，当r1>e1且r2>e2时，定理1成立.

2 局部稳定性和Hopf分支

系统(2)在正平衡点E*处的Jacobi矩阵为

(6)

其中：

则系统(2)的特征方程为

λ2+Aλ+B+(Cλ+D)e-λτ1+Ee-λτ2=0.

(7)

其中：

针对时滞的不同组合，考虑以下5种情形：

情形1τ1=τ2=0.此时系统(2)的特征方程(7)变为

λ2+(A+C)λ+B+D+E=0.

(8)

又因为A+C>0，根据Routh-Hurwitz准则，若假设：

(H1)B+D+E>0.

则系统(2)的正平衡点E*是局部渐近稳定的.

情形2τ1>0，τ2=0.此时系统(2)的特征方程(7)变为

λ2+Aλ+B+E+(Cλ+D)e-λτ1=0.

(9)

令λ=iω1(ω1>0)是该方程的根，代入到(9)式有

(10)

两边分别平方相加可得

(11)

p1=A2-C2-2(B+E)，q1=(B+E)2-D2.

(H2)p1>0，q1>0.

则(11)式无正根，因此方程(11)的所有根均具有负实部.进一步假设

(H3)q1<0.

(12)

(13)

对(9)式关于τ1求导，有

(14)

经计算得

(15)

如果(H5)成立，从而得到横截性条件

于是有如下结论：

定理2 对于系统(2)，当τ1>0，τ2=0，且(H1)成立时：

(1) 如果(H2)成立，则当τ1≥0时，系统(2)的平衡点E*是局部渐近稳定的.

(2) 如果(H5)成立，则存在一个τ10，使得当τ1∈[0，τ10)时，平衡点E*是局部渐近稳定的；当τ1>τ10时，平衡点E*不稳定；当τ1=τ10时，系统(2)发生Hopf分支.

情形3τ1=0，τ2>0.此时系统(2)的特征方程(7)变为

λ2+(A+C)λ+B+D+Ee-λτ2=0.

(16)

令λ=iω2(ω2>0)是该方程的根，代入到(16)式有

(17)

从而

(18)

p2=(A+C)2-2(B+D)，q2=(B+D)2-E2.

经计算p2>0，q2>0，则有

定理3 对于系统(2)，当τ1=0，τ2>0时，在(H1)条件下平衡点E*仍然保持局部渐近稳定.

情形4τ1=τ2=τ>0.

定理4 对于系统(2)，τ1=τ2=τ.当τ∈[0，τ30)时，平衡点E*是局部渐近稳定的；当τ>τ30时，平衡点E*是不稳定的；此外在τ=τ30处，发生Hopf分支.其中

(19)

证明同情形2.

情形5τ1>0，τ2>0.

考虑(7)式中τ1在稳定的区间，τ2作为参数.设λ=iω4为(7)式的根，代入到(7)式有

(20)

消去τ2，有

(21)

(H6) (21)式有有限个正根.

(22)

i=1，2，…，j，k=0，1，2，…

令

对(7)式关于τ2求导，有

(23)

经计算有

(24)

其中

T=2ω*cosω*τ*+Asinω*τ*+(C-τ1D)sinω*(τ*-τ1)-τ1Cω*sinω*(τ*-τ1).

又因为ω*E<0，假设

(H7)T<0.

则

由上述讨论，可得：

定理5 对于系统(2)，固定τ1∈[0，τ10)，若(H1)，(H6)和(H7)成立，则当τ2∈[0，τ*)时，平衡点E*是局部渐进稳定的；若τ2>τ*，平衡点E*不稳定；当τ2=τ*，系统(2)发生Hopf分支.

3 Hopf分支方向及其稳定性

研究在τ1=τ2=τ=τ30条件下，运用Hassard的中心流形定理和规范型理论，得到决定系统(2)的Hopf分支性质的表达式.

令u(t)=(u1(t)，u2(t))T∈R2，其中u1(t)=x1(τt)，u2(t)=x2(τt)，τ=τ30+μ，μ∈R，则系统(2)在C=C([-1，0]，R2)上变为一般的泛函微分方程

(25)

其中Lμ：C→R2，F：R×C→R2分别由以下形式给出：

(26)

F(μ，φ)=(τ30+μ)(F1(μ，φ)，F2(μ，φ))T.

(27)

这里：

φ=(φ1，φ2)∈C([-1，0]，R2)，

其中：

因此，由Riesz表示定理，能找到一个有界变差的二阶矩阵η(θ，μ)：[-1，0]→R2使得

(28)

这里

δ(θ)是Dirac-delta函数.

对于φ∈C1([-1，0]，R2)，定义

对于ψ∈C1([-1，0]，(R2)*)，定义A=A(0)的伴随算子A*：

双线性型：

设A和A*对应于特征根iω3τ30与-iω3τ30的特征向量分别为q(θ)和q*(s)，于是

A(0)q(θ)=iω3τ30q(θ)，A*(0)q*(s)=-iω3τ30q*(s).

通过计算，可以得到：

这里

利用文献[10]给出的算法，并用与文献[11-12]类似的计算过程，可以得到用于确定Hopf分支方向以及分支周期解稳定性的系数：

其中W20(θ)，W11(θ)的计算结果如下：

这就意味着

(29)

令C1(0)由(29)式给出，

(30)

易得出μ2，β2，T2的值.因此有

定理6 当τ=τ30时，(30)式的各个表达式中心式决定了分支周期解在中心流形上的性质，因此得出下面的结论：

(1)μ2确定Hopf分支的方向.如果μ2>0(μ2<0)，则Hopf分支是超临界的(次临界的).

(2)β2确定分支周期解的稳定性.如果β2<0(β2>0)，则分支周期解是稳定的(不稳定的).

(3)T2确定分支周期解的周期.如果T2>0(T2<0)，则分支周期解的周期增加(减少).

4 数值模拟

为了验证上面分析所得的理论结果，选择适当的参数，考虑以下系统：

(31)

当τ1>0，τ2=0时，条件(H1)和(H3)满足，通过计算有ω10≈0.900 8，τ10≈1.942 3，横截性条件满足.因此当τ1=1.8<τ10≈1.942 3时，平衡点E*是渐近稳定的(见图1)；当τ1=2>τ10≈1.942 3时，平衡点E*失去稳定性(见图2).

图1 当τ1=1.8<τ10≈1.942 3，τ2=0时，系统(31)的波图和相图

图2 当τ1=2>τ10≈1.942 3，τ2=0时，系统(31)的波图和相图

当τ1=τ2=τ时，B2-(D+E)2≈-1.165 2<0，系统有正根，通过计算可得ω3≈0.862 9，τ30≈2.190 9，C1(0)≈0.000 1-0.001 2i，μ2≈-0.000 1，β2≈0.000 2，T2≈0.002 4.

由定理6可知，系统(31)的Hopf分支是次临界的，分支周期解是不稳定的且分支周期增大.当τ=1.9<τ30≈2.190 9时，平衡点E*是渐近稳定的(见图3)；当τ=2.2>τ30≈2.190 9时，平衡点E*失去稳定性(见图4).

图3 当τ1=τ2=τ=1.9<τ30≈2.190 9时，系统(31)的波图和相图

图4 当τ1=τ2=τ=2.2>τ30≈2.190 9时，系统(31)的波图和相图

当τ1>0，τ2>0时，固定τ1=2.1，通过计算可得ω*≈908 6，τ*≈2.794 6.

(H7)T≈-2.801 2<0.因此当τ2=2.0<τ*≈2.794 6时，平衡点E*是渐近稳定的(见图5)；当τ2=3.2>τ*≈2.794 6时，平衡点E*失去稳定性(见图6).

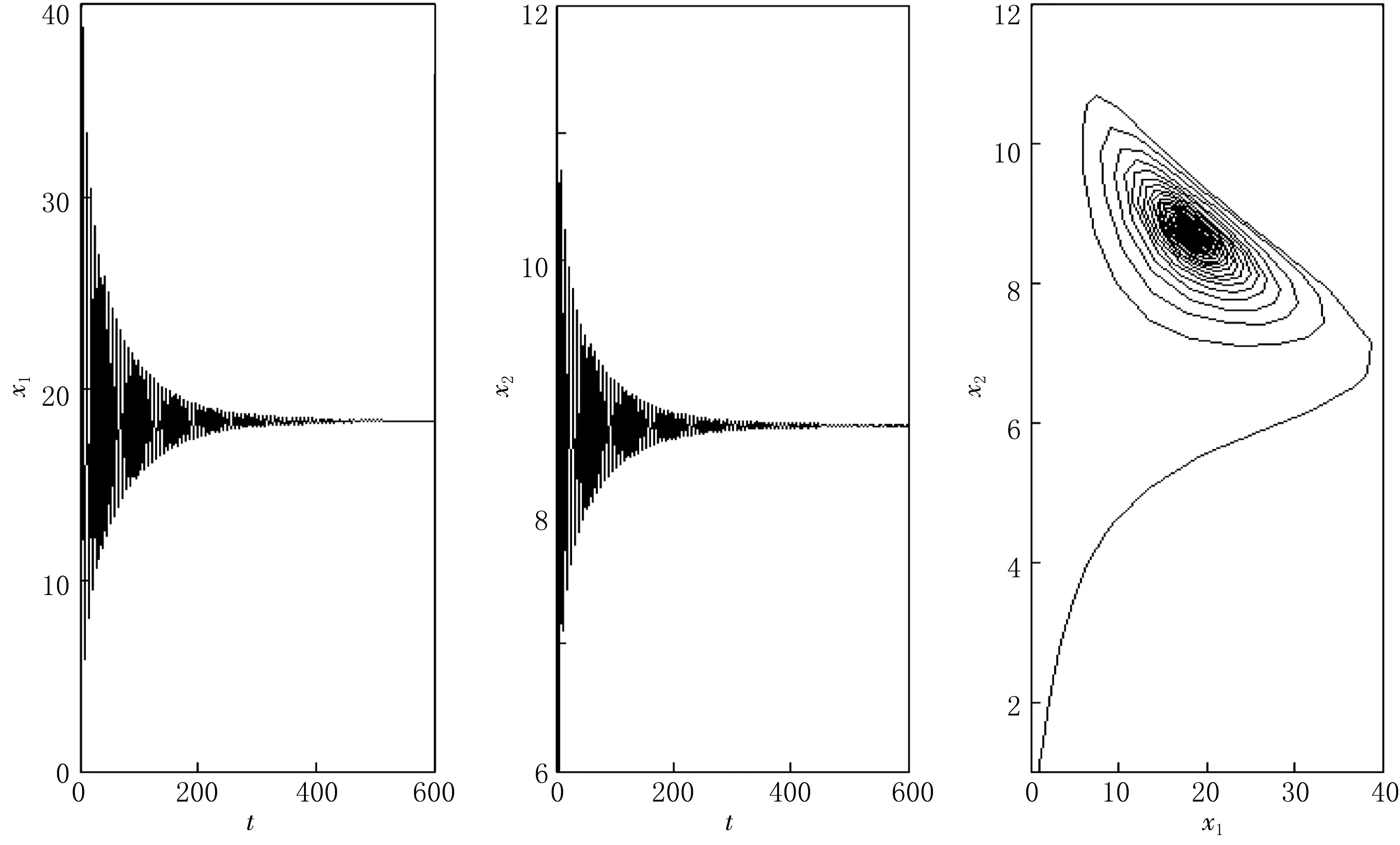
图5 当τ1=2.1，τ2=2.0<τ*≈2.794 6时，系统(31)的波图和相图

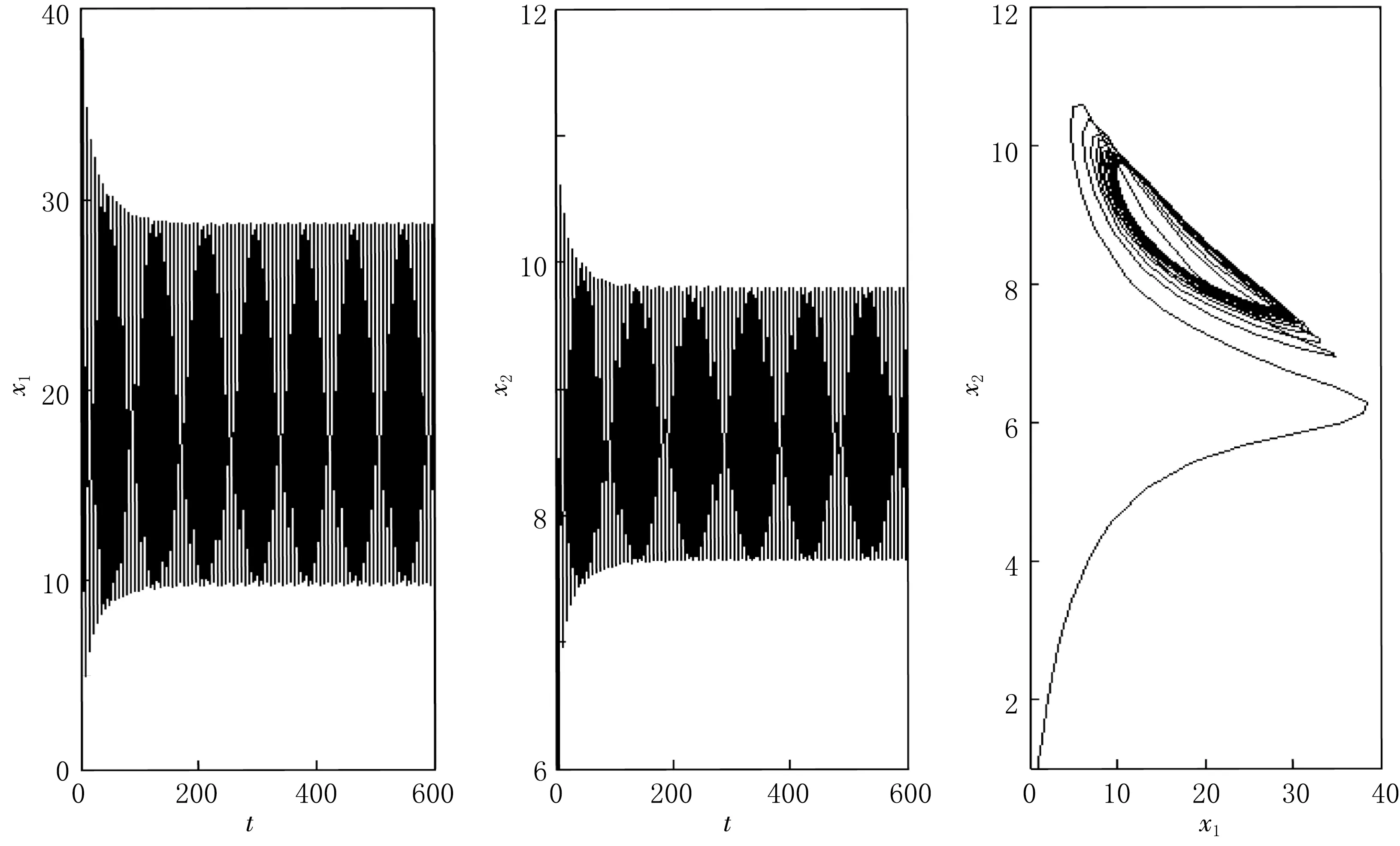
图6 当τ1=2.1，τ2=3.2>τ*≈2.794 6时，系统(31)的波图和相图

5 结论

本文研究了一类具有收获项的双时滞May合作系统.研究结果表明：当种群x1中只存在成熟期时滞τ2时，时滞变化对系统稳定性没有影响；当种群x1中只存在孕育期时滞τ1，或者当种群x1的两个时滞都存在时，种群的时滞变化对其生长具有很大影响.从图2、图4与图6中可以看出适当的延迟可以促进系统稳定性，而从图1、图3与图5中可以看出当时滞通过其临界值时，会破坏系统的稳定性，模型就会经历Hopf分支，产生周期解，甚至导致生态系统的失控与混乱.本文的研究有助于理解自然界中的一类种群合作关系，为相关部门及管理者规范对此类生物资源的开采、利用行为提供理论参考.