基于改进双向渐进法的轻量化设计方法

王颖　张争艳　雷焱阳　唐瑀　孙立新

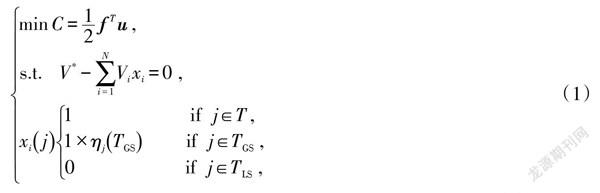
摘要 双向渐进法是近年来结构拓扑优化领域的一个热点，针对现有结构拓扑优化方法容易出现的网格依赖性和局部极值等数值不稳定现象，以及计算速率慢的问题，提出一种双重过滤增删的双向渐进法，简称为DBESO方法。该方法通过对典型的Michell结构、短悬臂结构和MBB梁结构进行不同过滤增删次数的计算，得出二次增删过滤为最佳的过滤增删次数，即在执行灵敏度过滤和单元的增删的基础上，将结果存入中间变量再对灵敏度过滤及单元的增删进行计算，并且设定一个判定结构性能的指标进行收敛。在MATLAB编程环境下，通过二维短悬臂结构和三维简支梁结构的拓扑优化算例，证明DBESO方法在保证力学性能不变的情况下，有效地提高结构轻量化的收敛速率，更好地抑制双向渐进方法的网格依赖性和局部极值等数值不稳定现象。

关 键 词 双向渐进法;轻量化;中间变量;灵敏度;MATLAB

中图分类号 TB21     文献标志码 A

Lightweight design method based on improved BESO method

WANG Ying， ZHANG Zhengyan， LEI Yanyang， TANG Yu， SUN Lixin

Abstract The Bi-directional evolutionary structural optimization method is a hot topic in the field of structural topology optimization. To solve the problem of slow iteration rate and numerical instability such as mesh-dependency and local minima in the existing structural topology optimization method， the paper proposes a Bi-directional evolutionary structural optimization method of double sensitivity filter and double addition and deletion （ DBESO）. In this method， through the different addition and deletion filtering of typical Michell structure， short cantilever structure and MBB beam structure were calculated. It is concluded that the second addition and deletion filtering is the best filtering addition and deletion times. The sensitivity filter and the element addition and deletion are calculated again through an intermediate variable after the implementation of the sensitivity filter and the element addition and deletion. And set an index to determine the performance of the structure of the convergence condition. By the topology optimization example of two-dimensional short cantilever beam and three-dimensional simply supported beam structure in MATLAB programming environment，verify under the condition of ensuring the same mechanical performance， the convergence rate of the lightweight structure is effectively improved and the numerical instability of the Bi-directional evolutionary structural optimization method is preferably eliminated.

Key words BESO; lightweight; intermediate variable; sensitivity; MATLAB

结构轻量化是目前研究轻量化方法的主要方向之一，其最大的分支之一是连续体结构轻量化。由于连续体结构广泛应用于工程中，因此对该理论的研究也较为广泛[1]。连续体结构轻量化主要包括尺寸优化、形状优化和拓扑优化。在尺寸和形状优化中，主要对截面特性和设计域边界进行优化。拓扑优化除了对设计域边界进行优化外，还规定了连续体结构中空腔的数量、尺寸和位置，并在工业领域，例如航空航天和汽车领域都存在有巨大的潜力[2-4]。近20年来连续体结构拓扑优化获得快速发展，成为工程创新设计的强有力工具。各种拓扑优化方法，例如密度法/各向同性实体材料惩罚法（solid isotropic material with penalization， SIMP）[5]、渐进结构优化法（evolutionary structural optimization， ESO）[6]、独立连续映射法 （independent continuous mapping method， ICM）[7]，基于几何边界描述的水平集方法（level set method， LSM）[8]，以及最近發展的移动可变形组件法（moving morphable components， MMC）[9]，都用来解决各种结构拓扑优化设计问题[10]。

其中，双向渐进结构优化方法（BESO）是在ESO方法和AESO方法综合的基础上提出的，不仅可以删除灵敏度值较低的单元，而且在结构的灵敏度值较高区域周围可以适当的添加单元，完善了ESO方法移除多余的单元后不能添加的缺陷。在近些年的BESO算法研究中，许多学者以目标函数灵敏度为基础，从不同的角度对单元灵敏度进行了改进[11]。Huang等[12]采用了考虑灵敏度历史迭代信息的方式，提高了灵敏度计算的精度。Huang等[13]利用插值策略提出了带有惩罚参数的灵敏度修正方法。Huang等[14-15]和Nguyen等[16]分别提出了基于增加位移约束和基于非线性材料的灵敏度计算公式。Ghabraie等[16]通过提高泰勒级数更准确地计算了单元灵敏度。孙艳想[17]研究了一种平滑处理技术的双向渐进结构拓扑优化。然而对于BESO方法容易出现的网格依赖性、局部极值等数值不稳定现象以及迭代速率慢的问题，目前还没有得到良好的解决。

综上所述，针对BESO优化算法计算过程中会导致数值不稳定现象，增删过程中易出现误差以及迭代速率较慢的问题，基于平滑处理技术的双向渐进法（SBESO），提出双重过滤增删的双向渐进方法（DBESO）。该方法是在灵敏度过滤和增删后重复进行灵敏度过滤和增删，并且设定一个测试结构性能的指标来进行收敛迭代，从而提高算法迭代的运算速率，消除数值不稳定现象，保障优化结果的稳定性和正确性。

1 优化模型的建立及灵敏度分析

1.1 数学模型的建立

改进的DBESO方法是在体积约束条件下，以最大静刚度为目标函数，优化问题的数学模型描述为

式中：[f]是结构的载荷矢量;[u]是结构的位移矢量;[C]是结构的平均静柔顺度;[V?]是结构的约束体积;[Vi]是每个单元的体积;[N]是结构离散后总的单元个数;[xi]是设计变量;[ηj（TGS）]是权重函数，选用的是线性函数[ηj（TGS）=αj+β]，将[TGS]区域的设计变量分划为0-1之间连续的数值，实现了算法计算过程中的平滑性和稳定性。

1.2 灵敏度分析

基于材料插值模型，使目标函数两边同时对[xi]进行求导，推导得出灵敏度计算公式为

式中，p表示为惩罚因子。当xi=1时，灵敏度数值的计算与p没有关系;当[xi=1×ηj（TGS）]时，p越大，单元的灵敏度数值也越接近于0;当xi=0时，灵敏度值为0。

2 DBESO方法的改进策略

2.1 灵敏度过滤方法

由于灵敏度过滤方法易实现且具有高效率性，所以本文的滤波技术采用灵敏度过滤方法。首先计算单元节点灵敏度的数值，节点灵敏度可以表示为

式中：[M]是与[j]节点有关的单元总数目;[ωi]表示[i]单元的权重因子，可以用下式表示：

式中，[rij]表示[i]单元中心到[j]节点的距离。当单元[i]越接近节点[j]时，[ωi]的数值越大，说明[i]单元的灵敏度对[j]节点的灵敏度影响越大。

然后，将节点的灵敏度值转换为单元的灵敏度值，设定某一单元为[i]单元，其灵敏度是通过以[i]单元中心为圆心，[rmin]为过滤半径的区域Ω内节点灵敏度的计算而获得的。Ω区域不随网格的大小的变化而变化，并且Ω区域应该包含至少一个单元。Ω区域的每个节点灵敏度都会影响[i]单元的灵敏度，因此，[i]单元的灵敏度可以表示为

式中：[K]表示Ω区域中的节点数;[ωij]代表权重因子。

2.2 单元的增加和删除策略

本文采用的增加删除策略是基于SBESO方法进行不断地改进而得到的。首先，对所有单元的灵敏度进行排序，划分成[n]个小组。然后根据灵敏度的大小设置阀值[αthdel]和[αthadd]，按照阀值把结构所有单元划分在3个区域[T]，[TGS]和[TLS]。如果满足[αi≤αthdel]，该单元归为[TLS]区域，如果满足[αi>αthadd]，该单元归为[T]区域，如果满足[αthdel<αi≤αthadd]，该单元归为[TGS]区域。最后，对[T]区域中的单元进行单元的添加，[TLS]区域中的单元完全移除，[TGS]区域的单元按照权重函数[ηj（TGS）]进行修改再判定是否增删。即将单元灵敏度划分成[n]个小组，定义[n]组中的p%单元完全被移除和增加，（1-p%）单元的移除和重新返回通过一个线性函数来实现如图1所示，单元密度的高低用一个权重函数[η（j）]来表示，[0≤η（j）≤1]。该函数用以判断[TGS]区域所有单元灵敏度的重要程度，当单元的灵敏度越大，那么对应的权重函数也就越大。这就表明，在下一次迭代中这些单元有可能会重新恢复到结构中，而当单元灵敏度越小，对应的权重函数就越小，下一次迭代中这些单元可能完全从结构中移除。

2.3 DBESO方法的改进策略

灵敏度过滤方法是当前处理棋盘格现象、局部极值和网格依赖性等数值不稳定现象的最有效手段，但依旧无法根除数值不稳定现象，只能在抑制该现象方法的基础上进行不断改进，更好地抑制该现象的出现。而单元的增删是对单元灵敏度进行排序，进而进行单元的增删。由于需要不断地添加和删除，所以出现误差的可能性较高。

本文针对上述问题，提出在一次迭代中进行多次过滤增删的方法，用以加强迭代过程中对数值不稳定现象的抑制作用，减少单元增删的误差。

由于进行多次过滤增删过多次会引起迭代速率减慢，局部极值变多的现象，需要通过研究设定最优过滤增删次数。由此设计1次、2次、3次等多次过滤增删，对其进行基于SBESO方法的优化迭代得到的结果进行对比，选用典型的Michell结构、短悬臂结构和MBB梁结构，几何尺寸分别为[L×D=96  mm×48  mm]、[L×D=80 mm×50 mm]和[L×D=120 mm×60 mm]，[F=100 N]，具體模型和作用力位置和方向如图2所示，其他初始条件不变，对3个数值算例的3种优化结果总结如表1所示。

通过表1可以看出，对Michell结构、短悬臂梁结构和MBB梁结构进行优化，最优结果随着灵敏度过滤增删次数的不断增加，网格依赖性的抑制作用明显得到了加强。通过3种数值算例的平均柔顺度变化曲线可以看出，在2次灵敏度过滤增删的情况下局部极值问题较好的得以解决。对于平均柔顺度值来说，随着灵敏度过滤增删次数的增多而越来越大，2次过滤增删的情况下柔顺度值还较为稳定，与1次灵敏度过滤增删相似，但3次灵敏度过滤增删的情况下，平均柔顺度值差距较大。并且，通过计算运算时间，可以得出单次运行时间在2次过滤增删时比1次过滤增删时增大了1%～6%，在3次过滤增删时比1次过滤增删时增大了6%～10%，可以看出，2次过滤增删对计算速率影响较小，所以选用2次过滤增删为最优的过滤增删次数。

综上所述，选用双重过滤增删的策略，设定中间变量[x?]，用来储存第1次过滤增删后的变量情况;然后将中间变量[x?]代入灵敏度计算公式中，按步骤进行第2次过滤增删;最后继续进行优化迭代的其他步骤。

2.4 收敛准则

虽然双重过滤增删会使其在迭代中数值不稳定现象得到很好的抑制，但在收敛速度方面并没有提高，所以需定义一个结构性能指标，来监控性能是否满足要求并且可以提高迭代速率。对于优化算法来说，由于体积和柔顺度是结构性能好坏的展现，所以，定义了一个和体积与柔顺度2个参数有关的性能指标来对结构性能进行监控。结构性能参数I的表达式如下：

式中：[Vi]是第[i]个迭代步骤结构的体积;[Vk+1]是第[i+1]个迭代步骤结构的体积。可以看出，[I]值越大，结构的性能越好。所以，用[I]来对该算法进行收敛。得出收敛准则为

式中：[Ii]是当前迭代步的性能指标;[Ii-1]是上一迭代步的性能指标;error是收敛因子。在结构满足式（8）的收敛准则时，结构获得最优拓扑结构，停止迭代。

3 改进DBESO方法优化流程

图3为双重过滤增删BESO（DBESO）方法的迭代流程图。由图3可以得出改进的双重增删过滤BESO（DBESO）优化方法的迭代流程为：

1）设定初始参数，建立有限元模型，设定负载和边界约束条件;

2）采用灵敏度公式计算每一个单元的灵敏度，进行灵敏度过滤和更新;

3）按照灵敏度的大小设定增删阀值，然后将单元依据灵敏度大小划分在3个区域T，TLS，TGS;对T区域中的单元进行添加，对TLS区域中的单元进行移除，按照权重函数[ηj（TGS）]对TGS区域的设计变量进行增删判定;

4）将增删结果设为中间变量[x?];

5）用[x?]进行灵敏度再过滤和更新，然后进行单元的再增删;

6）计算下一步迭代体积并更新单元设计变量;

7）计算性能指标，判定结构性能。

8）重复步骤2-7，在结构达到目标体积和满足收敛准则时，终止迭代。

4 改进DBESO方法数值算例验证

4.1 二维数值算例短悬臂梁结构

定义优化设计模型为二维短悬臂梁结构，其几何参数为[L×D=80  mm×50  mm]，材料的特性为杨氏模量为[2×105  MPa]，泊松比为0.3。边界约束条件和载荷如图2b）所示，左端固定，右端中点承受向下恒定载荷[F=100  N]。对结构采用80×50四节点有限元平面应力单元来离散结构，采用的权重函数为线性函数[ηj（TGS）=αj+β]。初始参数为：[V?=0.5]，[er=0.02]，[rmin=5 mm]，[penal=3]，[p=0.8]。

本文将该短悬臂梁进行120×76以及160×100的网格划分，结果如图4所示，对比图中结果，对于改进后DBESO方法网格数为80×50、120×76以及160×100的计算出的优化结果的网格是一样的，所以改进后的方法明显地减少了网格依赖性。对于改进前SBESO方法网格数为120×76以及160×100计算出的结果明显比网格数80×50计算出的结果网格数要多，网格依赖性严重，并且随着网格划分数的增大，优化结果的网格数越来越多。由此可以看出，改进后DBESO方法对于抑制网格依赖性等数值不稳定现象有了明显的提高。

为了验证改进后DBESO算法的优点，本文将基于改进前平滑的SBESO方法和改进后双重增删过滤的DBESO方法对该算例进行计算。在材料参数和约束条件不变的情况下，2种方法最终优化结果如图5和图6所示。并将2种方法结果以及不同网格划分下的结果进行总结对比，如表2所示。

观察图4、图5、图6和表2，可以得出以下结论。

1）对于平均柔顺度而言，在相同网格划分的情况下，改进前后2种方法的最终柔顺度值相近，改进前的平均柔顺度曲线有明显的数值波动，数值稳定性较差。改进后的平均柔顺度曲线比改进前的更为平滑，无明显的数值波動，较为平稳。

2）对于计算效率来说，在保持平均柔顺度相近的情况下，对于80×50网格划分的情况，改进后DBESO方法迭代速率提高了29%;对于120×76网格划分情况，改进后DBESO方法迭代速率提高14.4%;对于160×100网格划分情况，改进后DBESO方法迭代速率提高14.7%。

3）对于网格依赖性来说，相对于改进前优化方法，改进后方法在抑制网格依赖性方面有了明显的提高，减小了对零件的性能影响。

对于二维结构来说，改进的DBESO方法在提高计算效率方面以及抑制局部极值和网格依赖性等数值不稳定现象均有明显的优化。

4.2 三维数值算例简支梁结构

定义优化简支梁的尺寸为[50  mm×20   mm×4   mm]。模型如图7所示，其底面4个顶点为简支约束，顶面正中心施加垂直向下均布载荷[F=10 N]，密度[ρ=1 g/mm3]。将设计域划分为50×20×4的网格，材料特性有：[E=1  GPa]，泊松比[μ=3.0]，所需的参数为：[V?=0.5]，[er=0.02]，[rmin=3 mm]，[penal=3]，[p=0.9]。

本文将该短悬臂梁进行66×26×6以及60×24×4的网格划分，结果如图8所示，对比图中结果，对于改进后DBESO方法网格数为50×20×4、66×26×6以及60×24×4的计算出的优化结果的网格是一样的，所以改进后的方法明显地减少了网格依赖性。对于改进前SBESO方法网格数为66×26×6以及60×24×4计算出的结果明显比网格数50×20×4计算出的结果网格数要多，网格依赖性严重，并且随着网格划分数的增大，优化结果的网格数增多。由此可以看出，改进后DBESO方法对于抑制网格依赖性等数值不稳定现象有了明显的提高。

在MATLAB编写好的改进优化算法中，首先编写好该算例的有限元模型、边界条件、受力情况和位移约束情况，然后对改进前的SBESO方法和改进后的DBESO方法执行优化计算，得到改进前后最优结果图如图8所示，改进前后的平均柔顺度与迭代次数的曲线图如图9所示，改进前后的性能指标与迭代次数的曲线图如图10所示，对在不同网格划分下的两种方法结果总结如表3所示。

观察图8、图9、图10和表3，可以得出以下结论。

1）对于平均柔顺度而言，在相同网格划分的情况下，改进前后方法的最终柔顺度值相近，改进前的平均柔顺度曲线有明显的数值波动，数值稳定性较差，改进后的平均柔顺度曲线比改进前的更为平滑，无明显的数值波动，较为平稳。

2）对于计算效率来说，在保持平均柔顺度相近的情况下，对于50×20×4网格划分的情况，改进后DBESO方法迭代速率提高了1.8%;对于60×24×4网格划分情况，改进后DBESO方法迭代速率提高0.6%;对于66×26×6网格划分情况，改进后DBESO方法迭代速率提高9.5%。

3）对于性能指标来说，改进后的曲线比改进前的更为平滑，无明显的数值波动，较为平稳，改进前的曲线有明显的数值波动，数值稳定性较差，且迭代前后性能指标最终值相近。

4）对于网格依赖性来说，相对于改进前SBESO方法，改进后DBESO方法在抑制网格依赖性方面有了明显的提高。

对于三维结构来说，改进的DBESO方法在抑制局部极值和网格依赖性等数值不稳定现象有了明显的优化，且计算速率也有了小的提高。

5 结论

本文在现有SBESO方法的基础上，提出了双重过滤增删的DBESO方法。该方法是在原有过滤增删的基础上经过计算验证后，将结果存入中间变量，再进行双重过滤增删，并且在收敛时设定1个对结构进行性能判定的指标来进行收敛，用于提高收敛速率。通过二维短悬臂和三维简支梁结构作为数值算例进行计算，得出结果与现有的SBESO方法进行对比，验证了该DBESO方法的优越性和可行性。

1）对于网格依赖性问题，相较于SBESO方法明显的网格依赖性问题，可以看出改进后的DBESO方法更好的抑制了网格依赖性的问题。

2）对于局部极值现象，相较于SBESO方法的大的局部极值波动，改进后DBESO方法的迭代曲线更为平顺，几乎不存在局部极值问题。

3）对于计算结果与效率问题，相较于SBESO方法，改进后的DBESO方法的计算效率有了明显提高。

4）对于应用的广泛性来说，在二维和三维结构的优化中，改进的DBESO方法比SBESO方法在提高迭代速率和抑制网格依赖性、局部极值等数值不稳定问题方面有了明显的优化。

结果证明了改进的DBESO方法在二维结构和三维结构都明显优于原算法，更好地解决了数值不稳定导致的网格依赖性和局部极值等问题，且在迭代效率方面也有了提高。

参考文献：

[1]    宋武林. 三维连续体双向渐进结构拓扑优化[D]. 哈尔滨：哈尔滨工程大学，2017.

[2]    徐文鹏，苗龙涛，刘利刚. 面向3D打印的结构优化研究进展[J]. 计算机辅助设计与图形学学报，2017，29（7）：1155-1168.

[3]    LEDERMANN C，ERMANNI P，KELM R. Dynamic CAD objects for structural optimization in preliminary aircraft design[J]. Aerospace Science and Technology，2006，10（7）：601-610.

[4]    SHOBEIRI V. Topology optimization using bi-directional evolutionary structural optimization based on the element-free Galerkin method[J]. Engineering Optimization，2016，48（3）：380-396.

[5]    BENDS?E M P，SIGMUND O. Topology Optimization：Theory，Methods，and Applications[M]. Berlin，Heidelberg：Springer，2004.

[6]    XIE Y M，STEVEN G P. A simple evolutionary procedure for structural optimization[J]. Computers & Structures，1993，49（5）：885-896.

[7]    隋允康，葉红玲，彭细荣，等. 连续体结构拓扑优化应力约束凝聚化的ICM方法[J]. 力学学报，2007，39（4）：554-563.

[8]    WANG M Y，WANG X M，GUO D M. A level set method for structural topology optimization[J]. Computer Methods in Applied Mechanics and Engineering，2003，192（1/2）：227-246.

[9]    GUO X，ZHANG W S，ZHONG W L. Doing topology optimization explicitly and geometrically—A new moving morphable components based framework[J]. Journal of Applied Mechanics，2014，81（8）：081009.

[10]  SIGMUND O，MAUTE K. Topology optimization approaches[J]. Structural and Multidisciplinary Optimization，2013，48（6）：1031-1055.

[11]  劉娟. SIMP算法和BESO算法的关键技术研究[D]. 桂林：桂林电子科技大学，2016.

[12]  HUANG X，XIE Y M. Convergent and mesh-independent solutions for the bi-directional evolutionary structural optimization method[J]. Finite Elements in Analysis and Design，2007，43（14）：1039-1049.

[13]  HUANG X，XIE Y M. Bi-directional evolutionary topology optimization of continuum structures with one or multiple materials[J]. Computational Mechanics，2008，43（3）：393-401.

[14]  HUANG X，XIE Y M. Evolutionary Topology Optimization of Continuum Structures[M]. Chichester，UK：John Wiley & Sons，Ltd，2010.

[15]  HUANG X D，XIE Y M. A further review of ESO type methods for topology optimization[J]. Structural and Multidisciplinary Optimization，2010，41（5）：671-683.

[16]  NGUYEN T，GHABRAIE K，TRAN-CONG T. Applying bi-directional evolutionary structural optimisation method for tunnel reinforcement design considering nonlinear material behaviour[J]. Computers and Geotechnics，2014，55：57-66.

[17]  孙艳想. 基于BESO方法的结构动力学拓扑优化研究[D]. 哈尔滨：哈尔滨工程大学，2017.

收稿日期：2019-03-23

基金项目：国家自然科学基金（61802108）;河北省自然科学基金（E2017202296）

第一作者：王颖（1993—），女，硕士研究生。通信作者：孙立新（1964—），男，教授，Sunlixin100@126.com。