基于GeoGebra的一道课本习题的探究

王恩普

数学是研究数量关系和空间形式的一门科学，既有着无可替代的代数表达形式，又具备着更为直观的几何表达形式，而我们面对一些复杂的数形关系和复杂多变的几何位置关系时，很难抽象出其本质，难以被感官直接感知，更难被理解和深化，而信息技术，恰恰是解决这个问题的最好手段之一，它可以帮助我们探索规律启发思路，为解决问题提供直观，便于我们进一步解决问题，下面我们通过一道课本习题来谈一谈GeoGebra如何助力我们揭秘“真身”.

1 问题呈现

苏教版选修2-1第33页第11题：

准备一张圆形纸片，在圆内任取不同于圆心的一点F，将纸片折起，使圆周过点F（如图1），然后将纸片展开，就得到一条折痕，（为了看清楚，可把直线，画出来），这样继续折下去，得到若干折痕，观察这些折痕围成的轮廓，它是什么曲线？

对于这个问题，跟学生交流的时候，由于操作中的条件限制，不是反映的很清楚，毕竟这个轮廓是要在大量的直线中形成的，而不去动手，又无法在头脑中有这样的想象，毕竟，这是个动态的过程，如果我们连基本的轮廓都不清楚，更无法准确说明它是什么曲线了，其实这时候部分学生还认为，折痕围成的轨迹是图1中的线段CD的中点的轨迹，面对这些无法感知的困难，来看看GeoGebra（以下简称GGB）给我们带来了什么.

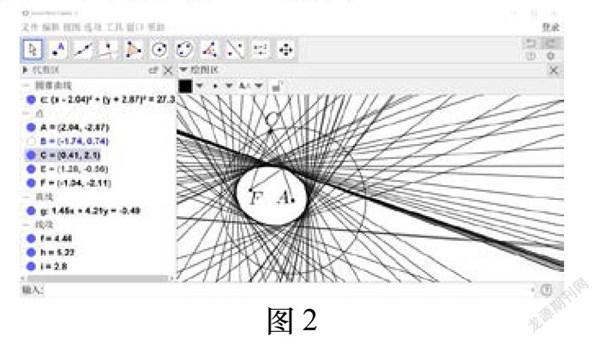
2 感知结果

如图2，在GGB中，我们进行下面的步骤：

步骤1首先点击上方的工具栏中的第五个工具箱，在工具箱中选择“圆（圆心和一点）”在绘图区画一个圆，在代数区显示为圆c，默认以C为圆心，B为半径.（也可以先用工具栏中的的第二个工具箱中的“描点”工具，在绘图区画出两个点A，B，这时候在下面的指令区输入：circle（A，B），即可得到以A为圆心，B为半径的圆）

步骤2由于B点是控制圆的半径的变量，我们可以选择隐藏，只需要在代数区中点B前面的蓝点点击一下便可隐藏，然后再选用“描点”工具在圆内画一个定点F.

步骤3这里需要说明的是，原题中的翻折过程中的直线，就是圆上动点和定点F所成線段的中垂线，所以我们在圆上再取个动点，注意圆上的动点是这样构造的，点击第二个工具箱的右下角的小箭头，选择其中的“对象上的点”，点击绘图区的圆周，即可得到图中的点C.（此方法得到的点只能在圆周上移动，也可使用指令：描点（c）.即可构造圆c上的动点）

步骤4选择第三个工具箱右下角的下拉箭头选择“线段”，再点击绘图区的点C和点F，构造线段C.再选择第四个工具箱中的“中垂线”，在绘图区点击线段（F，即可作出线段C的中垂线.

步骤5在绘图区右键点击中垂线，选择“跟踪”，这时候我们在圆上拖动点C，就会发现多条折痕包围成了图2中的形状——椭圆，

人工折纸怎么也达不到的视觉感知，GGB完成了，而且过程操作简单，清晰直观，也让我们可以比较容易的下结论，真正做到了“可见”.

3 结论证明

有了上面的结果，接下来我们可以大胆的将证明的方向指向椭圆，求轨迹的问题就转化为证明椭圆就是我们所求轨迹，且图中的A，F分别是椭圆的两个焦点，下面给出证明过程，

证明首先，记圆心为A，半径为r，定点为F，C为圆上的动点，由图3知所求轨迹上的任一点应该是椭圆与每一条中垂线的切点.设切点为Q，且设E是线段（F的中垂线上的任一点，则EC= CF，所以EF+ EA= EC+ EA，由题意知E在椭圆外（或上），所以EF+ EA≥EC+ EA，当且仅当E在椭圆上时取等号，同时当A，E，C三点共线时EC+EA最小，且此时EC+ EA=r，即EF+ EA=r，则有此时的E即为此时的切点Q，综上有QF+ QA=r，所以Q点的轨迹为以E，A为焦点的椭圆，

点评如果我们直接去证明所求轨迹是椭圆时，是比较困难的，但是如果我们知道了是一个怎样的椭圆时，然后结合椭圆的定义，再来说明图中呈现的椭圆即为所求，此处便豁然开朗了.

4 尝试探索

探索1原题中的F为圆内异于圆心的一点，如果F就在圆心，按照同样的折法，折痕围成一个怎样的轮廓呢？我们来看下GGB给我们呈现的结果：

从图4中可以清晰地发现，所求轨迹是以原来的圆心为圆心，r/2为半径的圆，这里的证明相对简单、清晰，此处就不再给出证明过程，由此，我们发现随着P点位置的变化，题中的轮廓也发生了变化，而当F点的位置移到圆上的时候，由于无法围成一个轮廓，此处不再讨论，

探索2原题中的定点F如果位于圆外时，按照同样的折法，折痕围成一个怎样的轮廓呢？按照题设的条件，GGB展示结果如图5：

从图5不难看出，结果呈现的是以F，A为焦点的双曲线，如果是以题中的折痕形成的轮廓来看，是圆内部的上述双曲线的一支，下面我们来证明为什么此时的双曲线即为所求的轮廓（靠近焦点A的那一支）.

证明如图6，首先，记圆心为A，半径为r，定点为F，C为圆上的动点，由图知所求轨迹上的任一点应该是双曲线与每一条中垂线的切点，设切点为Q，且设E是线段CF中垂线上的任一点，则EC= EF，所以EF - EA= E（： - EA，由题意知E在双曲线外（或上），所以EF - EA≤EC - EA，当且仅当E在双曲线上时取等号，同时当A，E，C三点共线时，EC - EA最大，且此时EC - EA=r，即EF - EA=r，则此时的E即为切点Q，综上有QF - QA=r，所以g点的轨迹为以E，A为焦点的双曲线的一支（靠近A点）.

点评上述证明过程是类比前面证明椭圆的过程，通过中垂线的性质，构造出到两定点的距离之差，进而利用双曲线的定义验证所观察的结论，这些问题解决的前提是GGB给我们提供的直观感知，

探索3苏教版选修2-1第14题：

将一张长方形纸片ABCD的一只角斜折，使点D总是落在对边AB上，然后展开纸片，得到一条折痕，（为了看清楚，可把直线，画出来），这样继续下去，得到若干折痕，观察这些折痕围成的轮廓，它是什么曲线？

和上面一样，我们先通过GGB来观察折痕所围成的轮廓，由图7知，轮廓是以D为焦点，AB为准线的抛物线，同样，我们来验证结论的正确性，

如图8，过E作线段AB的垂线，交线段ED的中垂线于点F，显然FD= FE，则点F在以D为焦点，AB为准线的抛物线上;另一方面，在中垂线上任取异于点F的G点，记G到AB的距离为d，则有GD= GE>d，所以G点不在抛物线上，而折痕与抛物线只有一个交点，即为F.综上可知，这些折痕围成的轮廓是以D为焦点，AB为准线的抛物线，

点评借助于GGB，我们看到了形的特征，进而我们又在“数”上给与了验证，让我们从中又感受了数形结合的数学思想.

5 技术释疑

在问题提出中提到有学生认为折痕是由线段CF的中点形成的轨迹，通过上面的图形验证以及结论证明，我们知道文首问题的最终轨迹并非来自于中点，那么又会产生新的疑问：随着C点的移动，线段CF中点的轨迹是什么呢？

图9和图10仅仅选取了点F在圆内和圆外的两种形式，可以看到随着C点的移动，CF中点最终形成的轨迹都是AF的中点为圆心，初始圆半径的一半为半径的圆，只是F点的位置决定了圆的位置，这里的证明比较容易，只需要取AF的中点和E相连，再连接A（，这里就不再进行证明，

点评在这样的探索中我们不仅真正地了解了折痕围成的轮廓，还认识了中点的轨迹，让我们很清晰地辨识出它们之间的差异.

6 结束语

当然我们还可以借助于GGB进行更多的探索，如果把文中的圆换成椭圆，或者换成双曲线，或者换成抛物线，折痕又是什么呢？在数学的学习过程中，我们会遇到许许多多的“不可见”，它们无法被感知，无法被呈现，而GGB正是发挥了它们的可视化优势，揭秘“真身”，揭示本质，突破数学因高度抽象概括的特性而带来的“难以意会、无法言传”之障碍，为我们的数学学习以及探索提供了极大可能，