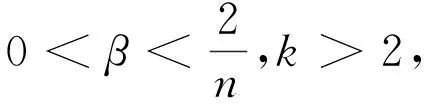一类具有奇异灵敏度和逻辑源的趋化
——消耗模型经典解的全局存在性

林金霞

(西华师范大学数学与信息学院，四川南充 637009)

其中Ω是Rn(n≥2)中的一个光滑有界区域，参数χ>0，μ>0，k>2，γ>0，r∈R,函数f(u)∈C1(R).在齐次Neumann边界条件下，对于弱消耗情况下的趋化模型，本文将证得其经典解的全局存在性.

0 引言

本文考虑如下具有奇异灵敏度和逻辑源的趋化-消耗模型：

(1)

1970年Keller和Segel[1]建立了经典的生物趋化模型，主要用于刻画细胞对趋化-交叉扩散产生的奇异反应的聚集行为.接下来将介绍一些关于细胞趋化模型的相关结果，

(2)

下面是一些关于具有奇异灵敏度的生物趋化模型的相关结论：

(3)

再次回到趋化-消耗模型：

{ut=Δu-χ∇·(uφ(v)∇v)+κu-μuk,x∈Ω，t>0

(4)

本文将考虑模型(1)，其主要目的是研究弱消耗对解的全局存在性的影响.本文假设参数χ>0,μ>0，r∈R，对于任意的s>0，函数f满足

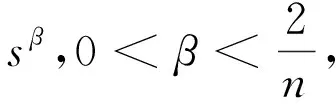
(5)

初始值满足

(6)

本文的主要结果如下：

定理1 假设Ω∈Rn(n≥2)是一个具有光滑边界的有界区域，在初始值满足(6)的条件下，当χ>0，μ>0，k>2，γ>0，r∈R，函数f满足(5)时，模型(1)的经典解全局存在.

1 相关引理

先介绍解的局部存在性.

引理1 假设q>n，f满足(5)式.那么对于任意满足(6)式的初始值(u0,v0)，都存在Tmax∈(0,∞]和如下一对唯一确定的函数对(u,v)

和

是模型(1)在区域Ω×(0,T)上的解，且使得当Tmax<∞时有

‖u(·,t)‖L∞(Ω)+‖v(·,t)‖W1,q(Ω)→∞,t→Tmax

(7)

此外，对于任意x∈Ω,t∈(0,T)存在：

u≥0,0

(8)

证明：通过运用适当的不动点框架和标准的抛物正则性理论[17-18]可以得到模型解的局部存在性，唯一性和(7)式的延拓性的结论.因为初始值满足(6)式，则可以利用类似于文献[19]的方法得到u≥0.因为u的非负性，则通过对模型(1)的第二个式子运用比较原则可以得到0

其次介绍本文会用到的一些不等式

(9)

为了证明定理，将给出以下一些先验估计.

引理3 假设(u,v)是模型(1)的一个解，指数k>2，那么存在常数m0,M1>0使得

(10)

和

(11)

成立.

证明：对模型(1)中的第一个等式进行积分并对其运用Hölder不等式可以得到

新乡贤统战：基层统战工作的整合拓展与全新模式——以浙江省县以下实践为案例 ……………………………………………… 许 军（4·76）

(12)

2 定理证明

(13)

以上假设易知w≥0.

接下来将通过证明w具有一个依赖于时间的上界，从而证得v有一个依赖于时间的下界.

引理5 令n≥2，函数f满足(5)式，则存在常数K3>0，使得

v≥C(t)=‖v0‖L∞(Ω)e-K3(1+t),(x,t)∈Ω×(0,Tmax).

证明：由模型(13)的第二个式子和(5)式可得

接下来对上式利用热半群估计[16]可知存在一个常数c1>0，使得

因此可以很容易证得‖v(·,t)‖L∞(Ω)≥‖v0‖L∞(Ω)e-c3(1+t),t∈(0,Tmax).

那么引理5就得证了.

引理6 令n≥2，函数f满足(5)式，则对任意的p>1都存在常数C0,C(T)>0使得

(14)

证明：结合模型(1)的第一个式子，对(up)t在Ω上积分可得

对上式运用Young不等式和引理5可推出，存在常数C(T)>0使得

通过整理有

(15)

(16)

(17)

首先，利用文献[22]中的方法对(17)式右边的第一项进行估计可得，存在常数c>0使得

(18)

然后，利用分部积分，Young不等式，不等式|Δv|2≤n|D2v|2和引理1对(17)式右边的最后一项进行估计

(19)

将(18)式和(19)式代入到(17)式中整理可得

(20)

引理7 令n≥2，函数f满足(5)式，那么对任意的p>0都存在一个常数C1>0使得

(21)

其中C0和C(T)均同于引理6中的C0和C(T).

证明：首先利用Young不等式对(21)式不等号左边的第一项进行估计可得，存在常数ε,c1,c2>0使得

(22)

(23)

联合(22)式和(23)式可得

(24)

其中c5=c2+c4.由引理1和引理2可得

令C1=c5，则引理7得证.

引理8 令n≥2，函数f满足(5)式，那么对于任意的p>1，都存在常数c6>0使得

‖u(·,t)‖Lp(Ω)+‖∇v(·,t)‖L2p(Ω)≤c6,t∈(0,T).

证明：结合引理7和引理8的式子可以推出

(25)

因为p>1，通过利用引理4和(10)式可得，存在常数c7,c8>0使得

(26)

将(26)式代入到(25)式可得

(27)

其中c11=C1+c10.则引理8得证.