时间分数阶Allen-Cahn方程的重心插值配点法
黄蓉, 翁智峰
(华侨大学 数学科学学院, 福建 泉州 362021)
基于自由能的概念来描述界面且已经被应用于许多带有界面问题的多相流系统中.最初的Allen-Cahn方程是以自由能的积分表示,是一种求解界面问题的数学模型,被广泛应用于平均曲率-流量[1]、晶体生长[2]、图像处理[3]、人群扩散现象[4]和材料科学[5]等研究中.近年来,分数阶算子的发展促进了非局部问题的迅速发展,将整数阶Allen-Cahn方程扩展到分数阶Allen-Cahn方程,已经引起众多学者的关注.汤涛等[7]首次证明了时间分数阶梯度流的能量耗散性和数值稳定性的分析;王宏等[8]采用快速Caputo算法结合傅里叶谱方法求解时间分数阶Allen-Cahn方程;杜强等[9]提出分数阶Allen-Cahn方程的凸分裂数值格式;刘欢等[10]基于SOE思想近似Caputo分数阶导数,提出时间分数阶Allen-Cahn的一种有限差分高效格式;张楠等[11]分别运用稳定化方法和SAV策略结合向后微分公式(backward differentiation formula,BDF)构造了时间分数阶Allen-Cahn方程和Cahn-Hilliard方程的高阶算法.任金城等[12]基于Laplace变换近似Caputo型分数阶导数, 从而求解偏微分方程; 汪精英等[15]利用Laplace变换与算子分裂法、差分法求解分数阶Allen-Cahn方程.采用Laplace变换近似分数阶导数,可有效地减少由于分数阶导数的历史记忆性所引起的储存量.
近年来,重心插值配点法作为一种新型的无网格计算方法,被广泛应用于求解各类微分方程.重心插值配点法成功地应用于求解平面弹性问题[17]、Fredholm方程[18]、整数阶Allen-Cahn方程[19-20].重心插值公式具有良好的数值稳定性,它能以机器精度任意逼近光滑函数,将Lagrange插值公式改进,并定义重心权,可得到重心Lagrange公式.重心插值公式具有计算量小、操作方便、易于编程、高精度、稳定性好等优点.重心插值配点格式求解微分方程的理论分析相对少.最近,文献[13-14]用重点插值配点法分别求解分数阶电报方程和热传导方程,并给出理论分析.
基于此,本文将分数阶Allen-Cahn方程通过Laplace变换近似为整数阶方程,在时间与空间方向均采用重心插值配点法求解整数阶方程,非线性项选取Newton迭代格式求解,并给出相容性误差分析.
1 分数阶Allen-Cahn方程的数值解
1.1 一维分数阶Allen-Cahn方程
考虑Caputo类型的时间分数阶Allen-Cahn方程,即
(1)
(2)
式(2)中,Γ(·)是Gamma函数.
Allen-Cahn方程的基本能量泛函E(u)为
(3)
E(u)关于时间t求Caputo型分数阶导数,即

(4)
显然,E(u)关于时间t具有非增长性,该方程满足能量耗散定律.
1.2 将分数阶方程通过Laplace变换转变为整数阶方程
一维Allen-Cahn方程中的分数阶导数可利用Laplace变换逼近,即
(5)
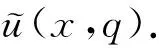
将qα在区间(0,1]作线性插值,并代入式(5),即
(6)
对式(6)采用Laplace逆变换,并代入式(1),推出整数阶方程,即
(7)
(8)
1.3 重心插值配点法求解Allen-Cahn方程

(9)

(10)
(11)
1.3.2 重心有理插值 考虑重心有理插值配点法的基函数.给定n+1个插值节点a=x0 (12) 将Zk(x)以Lagrange公式改写,即有 (13) (14) 由式(12)~(14)可推出重心有理插值公式,即 (15) 1.3.3 重心插值配点法求解Allen-Cahn方程 考虑整数阶Allen-Cahn方程的重心插值配点法计算格式,其方程变形为 (16) 式(16)中:(x,t)∈[a,b]×[0,T],G(u)=u(u2-1). 区域Ω=[a,b]×[0,T],在空间[a,b]上取m+1个节点a=x0 考虑上述热传导方程,先固定t,考虑变量x,则u(x,t)在节点x1,x2,…,xm上的重心插值公式为 (17) 类似,固定x,考虑变量t,则u(x,t)在节点t1,t2,…,ts上的重心插值公式为 (18) 式(18)中,φj(t)为t方向上的插值基函数. 由式(17),(18)可知,u(x,t)在节点{(xi,tj),i=0,1,…,m,j=0,1,…,s}上的重心插值为 (19) 考虑u(x,t)对变量x,t求l+k阶偏导数,即有 (20) 上述偏导数在节点(xr,tp)处的函数近似值为 (21) 因此,式(16)的重心插值配点法的计算格式为 上式可改写成微分矩阵形式,即 (23) 设函数u(x,t)运用重心Lagrange插值法逼近的数值解为pm,s(x,t),定义误差函数e(x,t)=u(x,t)-pm,s(x,t).引用文献[13]中的重要定理. 引理1若u(x,t)∈C(n+1)(Ξ),Ξ=[a,b]×[0,T],n=max{m,s},定义的e(x,t)成立.即 (24) (25) 根据引理1可推出定理1. (26) 证明非线性项G(u)满足利普希茨条件,则存在常数K>0,成立 |G(u(x,t))-G(u(xm,ts))|≤K|u(x,t)-u(xm,ts)|. (27) 由式(1),(8)可知 (28) 由引理1可知:R1=ut(x,t)-ut(xm,ts)=et(x,ts)+et(xm,ts),可推出 (29) 同理,可得 (30) 阿玉奇是土尔扈特汗国开创者书库岱青之孙、朋楚克之子,生于1642年,卒于1724年2月19日,享年81岁,执政50余年。阿玉奇汗是土尔扈特历史上著名的汗王,他执政期间,由于他卓越的统治才能、高超的外交策略,以及辉煌的武功战绩,不仅造就他本人一生的丰功伟业,使他成为当时遐迩闻名的游牧汗国领袖,同时也将土尔扈特国推向前所未有的鼎盛阶段。托忒文历史文献《卡尔梅克诸简史》中曾对阿玉奇汗作过如下评述:他一生“帮助了许多国家和部落,没有让卡尔梅克人衰弱和受欺。让他强盛者尊重他,与他相衡者惧怕他。名义上是俄罗斯臣民,但一切事情均由自己做主,所以,他是伏尔加河卡尔梅克汗中最有威望的一位”。 注1据文献[14]的重要定理,类似定理1的推导,易知采用重心有理配点法求解整数阶Allen-Cahn方程的误差分析如下. 定理2设u(x,t)∈Cμ1+2[a,b]×Cμ2+2[0,T],u(xm,ts)是u(x,t)运用重心有理配点法求解的数值解,成立Du(xm,ts)=0,非线性项G(u)满足利普希茨条件,则 |u(x,t)-u(xm,ts)|≤C(hμ1-1+τμ2). (31) 考虑Allen-Cahn方程的非线性项G(u),在u0处泰勒展开,可得 (32) 从而,式(23)的Newton迭代格式为 (33) 由节1.3和节1.5可知,整数阶Allen-Cahn方程在重心插值配点法下的计算格式为 (34) 为了验证数值格式的准确性,选取如下一维Allen-Cahn方程.即 (35) 式(35)中:精确解u(x,t)=(1+t3)sin(1.5πx), (x,t)的取值范围为[0,1]×[0,1].则有 取空间节点M=30,时间节点N=20,在ε=0.3,α=0.5下方程的精确解与误差分布,分别如图1,2所示.由图1,2可知:两种重心插值配点法的数值解图像均与真解图像逼近,且具有较高的精度. (a) 精确解 (b) 误差分布图1 重心Lagrange插值配点法的数值解与误差分布图像(α=0.5)Fig.1 Numerical solution and error distribution images of barycentric lagrange collocation method (α=0.5) (a) 精确解 (b) 误差分布图2 重心有理插值的数值解与误差分布图图像(α=0.5)Fig.2 Numerical solution and error distribution images of barycentric rational collocation method (α=0.5) 在ε=0.3下,分别选取不同的剖分节点数和不同的α,利用两种重心插值配点法计算Er(M,N),结果如表1所示. 表1 两种重心插值配点法求解方程的最大相对误差(ε=0.3)Tab.1 Maximum relative error of solving equations by two barycentric interpolation collocation methods (ε=0.3) 由表1可知:当选取不同的α时,该配点格式采用较少的节点数,数值解可达到高精度;网格剖分越细,数值精度更高.与文献[15]中的经典差分法比较,当剖分节点数为M=50,N=2 500,最大相对误差可达到10-3量级;文中提出的重心Lagrange配点法格式选取节点M=6,N=6,最大相对误差就达到10-4量级,重心有理配点法格式选取节点M=4,N=4,最大相对误差可达到10-3量级.数值算例表明,两种重心插值配点格式剖分较少的节点就能达到很高的精度. 一维Allen-Cahn方程的离散能量函数如下 (37) 选定初值u(x,0)=ε·sin(1.5πx),取Dirichlet的边界条件,左边界为u0=1, 右边界为uM=-1,t∈[0,2];结合式(37),令网格剖分为M=30,N=20,固定ε=0.3,α分别取0.2,0.5,0.9,则两种重心插值配点法的能量递减,如图3,4所示. (a) 重心Lagrange插值配点法 (b) 重心有理插值配点法图3 不同插值配点法的能量递减图Fig.3 Energy decline images of different interpolation collocation method (a) 重心Lagrange插值配点法 (b) 重心有理插值配点图4 不同插值配点法的数值解图像(α=0.2)Fig.4 Numerical solution images of different interpolation collocation method (α=0.2) 从图3可知:当α取不同值时,时间分数阶Allen-Cahn方程的能量耗散特性;当t增加时,能量泛函E(u)随之递减,最终趋于稳定状态.系统的能量耗散速度随着分数阶阶数α不同而变化,α越小,能量衰减越快.此外,E(u)的曲线受剖分细密程度影响,剖分变细,图像更光滑.从图4可知:两种重心插值配点法的数值解图像均与真解图像逼近. 利用Laplace变换近似Caputo型分数阶导数,将分数阶Allen-Cahn方程转化为整数阶问题;在时-空方向均利用重心插值配点法离散求解整数阶Allen-Cahn方程,并给出配点法格式的相容性误差分析.数值算例结果表明,与文献[15]中的有限差分格式比较,该重心配点格式剖分少量节点数即可达到格式的高精度,并满足能量耗散规律.该方法可以广泛推广到求解其他时间分数阶微分方程.1.4 相容性分析




1.5 基于牛顿迭代的Allen-Cahn方程
1.6 一维Allen-Cahn方程在重心插值配点法下的计算格式
2 数值算例

2.1 算例一



2.2 算例二


3 结束语

