紧连通李群的闭测地线

张 乾

广西师范大学数学与统计学院 广西桂林 541000

1 概述

闭测地线是处处光滑且具有周期性的测地线，在常见的闭曲面中例如Sn上的闭测地线就是以它的球心为圆心的大圆即S2。在流形的测地线的研究中，Vakhrameev[1]证明了某一类流形的闭测地线一定存在，实际上如果对于基本群非平凡的黎曼流形能够推广成一定存在不可缩的闭测地线。文献[3]中给出了单连通紧流形的闭测地线的性质的刻画。Borisenko[2]研究了球面空间的一些闭测地线。段华贵[3]研究了一类Finsler流形的闭测地线。

另一方面，J.Cheeger和D.Ebin在文献[4]中给出了黎曼流形里测地线与李群中的单参数子群之间的关系，证明了具有双不变黎曼度量的李群即紧李群上的测地线一定是其单参数子群或单参数子群的合成。Hopf-Rinow定理[5]则说明了测地完备的黎曼流形中的任意元素必落在它的一个单位元素出发的测地线上。詹华税[6]对李群的基本性质做了很好的总结。Lucas Seco[7]限制在紧李群上对紧李群的测地线做了一些计算，我们自然就想进一步研究紧李群上的闭测地线的结构。

Cartan定理[8]则告诉了我们对任意的紧李群G，它的Cartan子群不仅彼此共轭，并且这些Cartan子群的并就是G。而根据紧交换李群的分类，我们又知道了Cartan子群是一个环面，即G是一个极大环面，若它的极大环面是T1，我们知道它就是一条闭测地线。由于紧连通李群自然的具有双不变度量，是完备的黎曼流形，那么在Hopf-Rinow定理[9]的基础上，我们自然会猜测，如果是紧连通李群，其上的元素能否落在从单位元出发的闭测地线上。在《李群和李代数》[10]提到：设李群G的李代数为ɡ，则存在ɡ中包含原点的开集V，使得exp|v：V→exp(V)是解析同胚。综合上面的猜测我们也会自然的思考李群上局部的解析同胚在紧李群中多大程度能扩大到整体。在本文我们根据以上的猜测对紧连通李群的闭测地线的拓扑做了一定的描述，计算了它的基本群以及各阶同调群并给出了下面这一结论：

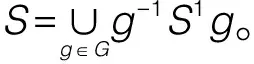
本文的结构如下，在第一节我们将回顾一下李群以及黎曼流形里的部分定义与结论，在第二节我们将完成所给出定理的证明。

2 基本概念和引理

2.1 几何的相关定义与结论

我们设(M，g)是m维黎曼流形，为M上的黎曼联络，M上的一条参数化曲线是一个光滑映射γ：I=(a，b)→M，M上沿γ的向量场V是一个映射。如果沿γ的向量场V满足：∇γ′V=0，则称V是沿γ平行的。

定义1 若γ的切向量γ′沿γ是平行的，即∇γ′γ′=0，则称曲线γ为M上的测地线。我们称γ是闭测地线，指γ是度量下g的测地线，而且具有周期性。

注1 这里的周期性指γ是处处光滑的闭曲线。如果γ：[a，b]→M是测地线，它的长度L[γ]=ρ(γ(a)，γ(b))，我们称γ是极小测地线。

定义2 expp：B(⊂Tp(M))→M称为关于点p的指数映射，其中B是点p的一个邻域。

指数映射的几何意义是沿γ由p到γ(1)=expp(v)的弧长，若它有意义，则expp(v)总是唯一确定的。

定义3 如果对于所有的p∈M以及所有的V∈Tp(M)，expp(V)都是有意义的，则称M是测地完备的。

对测地完备的黎曼流形，有以下结论，证明详见《RiemannianGeometry》[5]：

引理1(Hopf-Rinow)下列叙述等价：

(1)M是测地完备的；(2)M是具有距离ρ(p，q)=inf{L[σ]|σ(a)=p，σ(b)=q}的完备度量空间；(3)对某个p∈M，expp是在整个Tp(M)上定义的。

由上述的任意一条可推出下列结论：(4)M的任意两点都能由极小测地线相连。

2.2 李群的相关定义与结论

设X∈ɡ，由X可以构造G上的微分方程：

曲线σ(t)，t∈(a，b)是微分方程的解曲线。由微分方程的理论我们知道这个初值方程的解在局部上存在唯一并且解析。这个方程的解就是G的单参数子群[5]，其与G的李代数ɡ中的元素一一对应。关于单参数子群有一个重要的结论：

引理2 对于紧李群G，它的测地线是其单参数子群或单参数子群的合成[10]。

注2 实际上在紧李群G上存在双不变黎曼度量，即在这种度量下左平移与右平移都是G的等距变换。

注3 由上述的Hopf-Rinow定理知紧李群G上的任意一点都能用测地线与原点相连，而这条测地线也必定是G的一个单参数子群，即G的每一个元素必落在G的一个单参数子群上。

定义4 设G是李群，它的李代数为ɡ，定义映射exp：ɡ→G，Xσ(1，X)称为G的指数映射。

任意选取原点处的切向量X∈ɡ，则它是ɡ中曲线tX的切向量，而指数映射将tX映为单参数子群exp(tX)。指数映射与李群同态满足以下交换图表：

注4 上述图表表明对李群G的李代数ɡ，则存在ɡ中包含原点的开集V，使得exp|v：V→exp(V)是解析同胚。

对紧李群我们有：

G中Cartan子群T是其极大连通交换李群。根据紧连通李群的分类[8]我们可以知道T是环面。Cartan定理的证明可以详见《李群讲义》[8]。根据Cartan定理我们知道紧连通李群G的Cartan子群彼此共轭，并且这些Cartan子群的并就是G。

3 主要结果

定理1 对于紧连通李群的Cartan子群Tn，若n=2，设在单位元e处的闭测地线与水平方向的夹角为θ，那么其上的所有经过e的闭测地线都满足tanθ为有理数。

证明 考虑环面的商映射。

其中v1和v2是T2中的闭测地线从单位元e出发的两个方向向量。在商映射下，闭测地线形如：

令vi与v2的夹角为θ，根据定义1，vi处处平行，则vi与v2的交点的个数等于vi绕着v1方向的闭测地线转的圈数，又因为闭测地线具有周期性，从而这个圈数必为整数。那么，tanθ一定是有理数。

推论1 对于任意的正整数n，从单位元e出发的闭测地线的方向向量vi与vj的夹角为θ，vj是与环面上的任意大圆的方向向量，则tanθ为有理数。

定理2 任取Tn上点a，对任意ε>0，存在过单位元e的闭测地线构成的集合中的一点p，使得ρ(a，p)<ε。

证明 由引理1可知，存在极小测地线连接a，p两点。那么我们先考虑n=2的情形。根据定理1，tanθ为有理数，考虑环面的商空间，则其上的有理格点集是其上通过单位元e的闭测地线集的子集。根据R2上的有理格点的稠密性即得。当n>2时同理。

推论2 紧连通李群G上过单位元e的闭测地线集是可数个闭测地线的并。

我们现在可以知道这些闭测地线构成的集合的拓扑，但在计算它的基本群之前我们仍需下面引理：

引理4 如果(Mn，g)是紧黎曼流形并且π1(Mn)≠0，则(Mn，g)有不可缩的闭测地线。

定理3 我们令紧连通李群G上过单位元e的闭测地线为S，这些可数个闭测地线记为σ1，σ2，σ3，…则S的基本群是σ1，σ2，σ3，…的自由积。

证明 由引理4知道S中存在不可缩的闭测地线，从而它的基本群非平凡。由引理3可知G是他的极大环面的共轭类的并。在定理1和定理2中我们可以知道Tn中的过单位元e的闭测地线集的拓扑结构，而G是有限个共轭于Tn的极大环面的并，故紧连通李群G上通过e的闭测地线集的拓扑与Tn相同，那么它的基本群即得。

定理4 设G上过e的闭测地线集为S，那么:

证明S上所有闭测地线至少交于单位元e，即S是连通集，则H0(S；Ζ)=Ζ。根据Van-Kampen定理，S的一维同调群就是它的基本群的交换化，那么H1(S；Ζ)=Ζ∞。S上并不存在二维及以上的闭链，故其他维数的同调不存在。

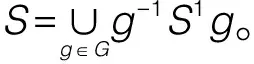
证明 我们先说明S中的闭测地线一定是G的单参数子群。由于环面是测地完备的，根据引理2.1可以知道环面上的任意点a与e之间有一条极小测地线相连。而若有S中的闭测地线S′经过a与e两点，那么由定义可知其上的任意位置的切向量方向相同，故该条闭测地线不可能是单参数子群的合成，只可能是G中的一个单参数子群。

我们接下来仅需证明α∈S，存在g∈G使得α∈g-1S1g。对任意α∈S，不妨设α过e与p，其中p∈G且p≠e。由Cartan定理可知G上任一元素共轭于其Cartan子群中的某个元素。从而有存在t∈T使得p=g-1tg，其中g∈G。由引理1可知e与t之间存在极小测地线相连，由单参数子群的定义可知其在整个切空间均有定义，且沿原来方向不变，从而这样的一条极小测地线所对应的单参数子群也是一个闭子群。不妨设β∈S1，其中β经过e和t。设α所对应的G的子代数是g1，β所对应的G的子代数是g2。考虑如下的交换图表：

由图可知g-1βg是闭测地线。由测地线的唯一性可知α=g-1βg，即α∈g-1S1g。证毕。