采用谱单元Galerkin法求解非线性模态

李 诚，李鸿光

（上海交通大学 机械系统与振动国家重点实验室，上海 200240）

非线性模态理论作为非线性振动研究的一个重要分支，是线性模态理论在某些非线性振动系统中的一种对应拓展。自Ronsenberg 引入非线性模态NNM(Nonlinear Normal Modes)的概念以来，国内外不少学者在非线性模态的定义、动力学特性以及非线性模态的求解方法等方面都做出了重要贡献。Ronsenberg首先将非线性自治保守系统中各个自由度的同步周期运动模式定义为非线性模态[1]。Shaw和Pierre 引入不变流形的概念定义非线性模态。不变流形定理表明，非线性系统的不变流形与派生线性系统的不变子空间相切于系统平衡点，该不变子空间为派生线性系统的线性模态。系统发生在不变流形上的运动即为非线性模态运动[2]。吴志强和陈予恕发展了该思想[3]，定义非线性模态为系统模态空间中偶数维不变流形上的运动，通过求解系统动力学方程的规范型(Normal Form)来构造非线性模态的控制方程，根据方程将非线性模态分为非耦合模态和内共振模态。在该定义的基础上，李欣业等[4]对多自由度内共振非线性系统中内共振模态的分岔特性进行了研究。徐鉴等[5]研究了系统在非奇异条件下非线性模态叠加解的有效性与模态动力学方程静态分岔的关系。Cirillo 等[6]发现了非线性模态与Koopman 算子谱特性之间的关系。非线性模态的求解方法包括Nayfeh 等采用的多尺度法[7]、Vakakis等[8]提出的一种基于能量的幂级数展开渐近解法，文献[9－10]中采用的规范型方法等。Shaw和Pesheck等应用非线性模态的不变流形的定义，采用了相应的基于幂级数展开的渐近解法[11]，更进一步提出了基于Galerkin法的半解析方法[12]。Galekin法的求解精度一般均优于基于摄动法的渐近展开解，尤其在非线性系统响应幅值较大时，Galerkin法在精度上更具有显著优势。对于保守系统非线性模态所对应的一系列周期运动可采用打靶法等相关改进算法[13－15]，结合延拓连续法获得一系列数值解。

非线性模态的曲面几何结构可用来描述非线性系统发生模态运动时各自由度之间的相对关系[16]。对于动力系统的非线性模态，更高的求解精度可以更准确地揭示系统在非线性模态运动时各部分之间的耦合动力学特性。本文提出了一种基于谱单元的Galerkin 法以求解不变流形定义下的非线性模态曲面。以一个两自由度非线性系统为例，指出在求解非线性模态时已有的Galerkin分片方法所求解区域较大处解的精度仍可能存在不足。基于谱单元的Galerkin 法可获得整体上更高精度的非线性模态曲面解。

1 不变流形定义下的非线性模态微分方程

考虑保守非线性系统在其广义模态坐标下的控制方程：

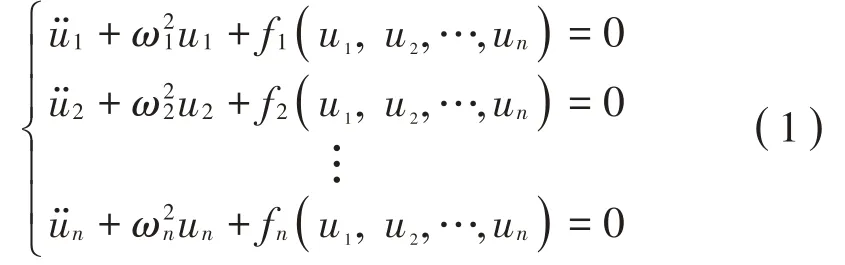
方程组中ui(i=1,2,…,n)是系统投影到派生线性系统模态空间上的广义模态坐标，ωi即为系统第i阶线性模态的固有频率，设作用在该阶模态振子上的回复力fi为广义模态坐标位移向量ui的非线性光滑函数。假设各模态振子之间未出现内共振，根据非线性模态所采用的不变流形的定义，系统第M阶非线性模态的运动中各自由度之间满足如下的约束关系：

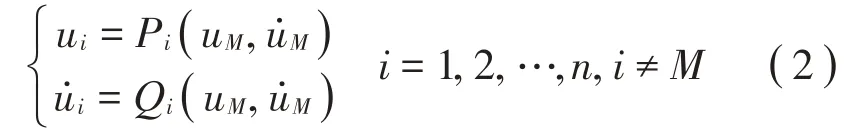
第M阶模态坐标uM、为该阶非线性模态的“主自由度”，其余坐标ui、(i≠M)为对应的“从自由度”，各个从自由度和主自由度之间在非线性模态运动中满足式(2)的约束关系。文献[12]对主坐标对引入一种极坐标变换，将主坐标对(uM,) 转换为(a,φ)：

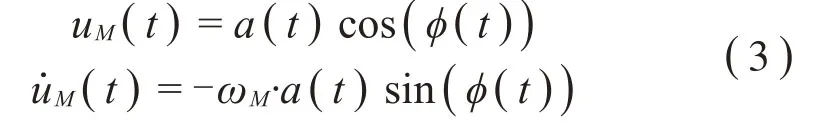
主坐标对的控制方程化为：

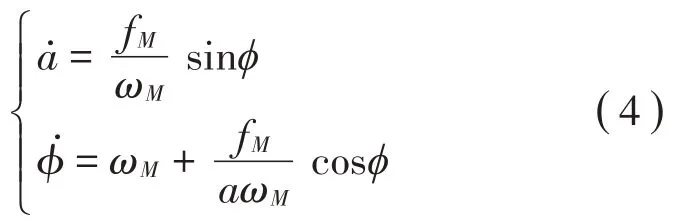
待求的非线性模态的约束关系式(2)变为：

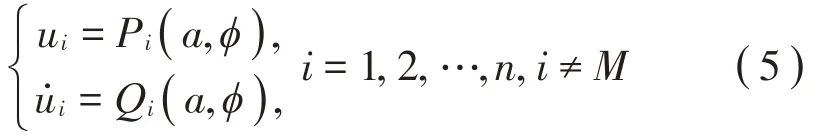
之所以先引入该极坐标变换，是因为非线性模态的不变流形曲面一般是关于主坐标中的相角φ在[0,2π]上的周期连续函数，其半解析解便可假设为关于φ的谐波函数的展开式。将式(5)分别代入方程组(1)中各个从自由度振子的微分方程对应的1阶微分形式，应用链式法则得：

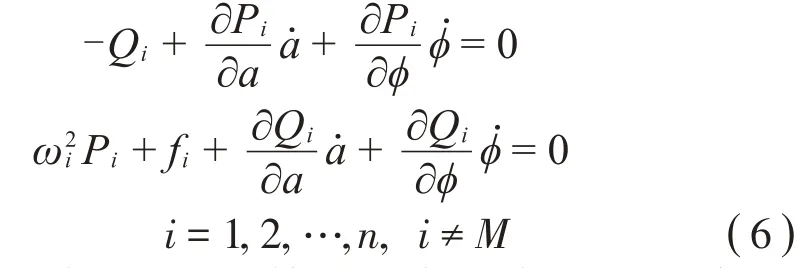
将式(4)代入式(6)，等式两边同乘以a以避免解在a=0处的奇异性，最终得到不变流形定义下第M阶非线性模态的控制方程：

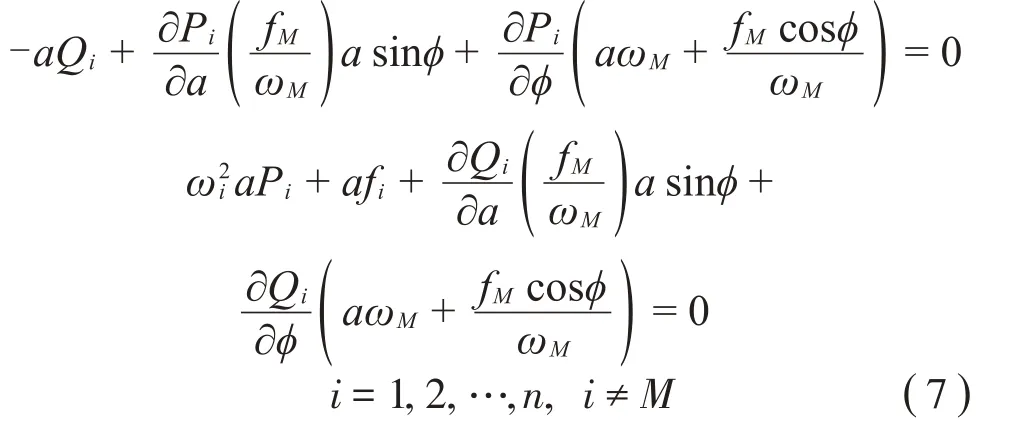
2 求解非线性模态的Galerkin法

针对非线性模态不变流形的微分方程式(7)，假设解为展开式(8)：

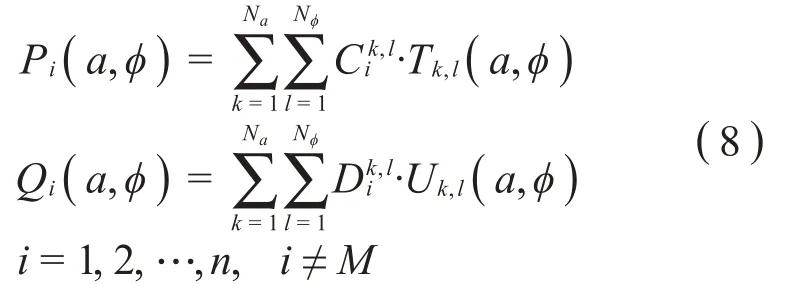
Pi(a,φ)、Qi(a,φ)为关于主坐标对a和φ的未知函数，展开式中各项基函数的待求系数为C和D，关于a和φ的基函数的个数分别为Na和Nφ。在求解域{(a,φ)|a∈[0,a0],φ∈[0,2π]}上应用Galerkin 法，将式(8)作为假设解代入后将该余量式选取为T(a,φ)，U(a,φ)作为试函数，令积分式为0，得式(9)、式(10)：

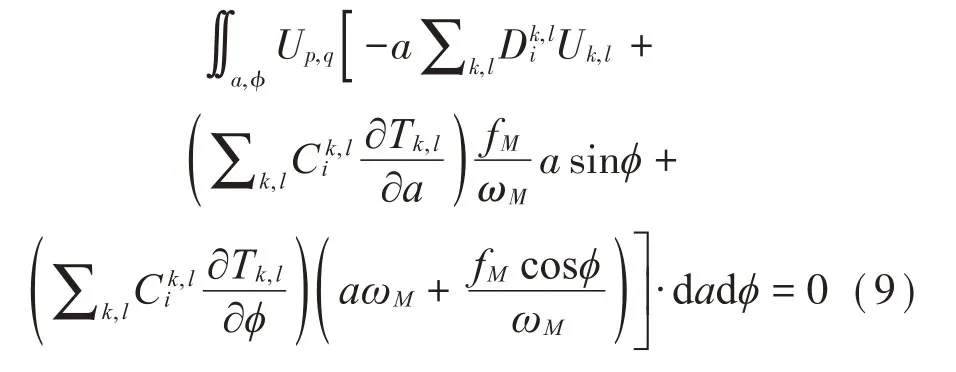
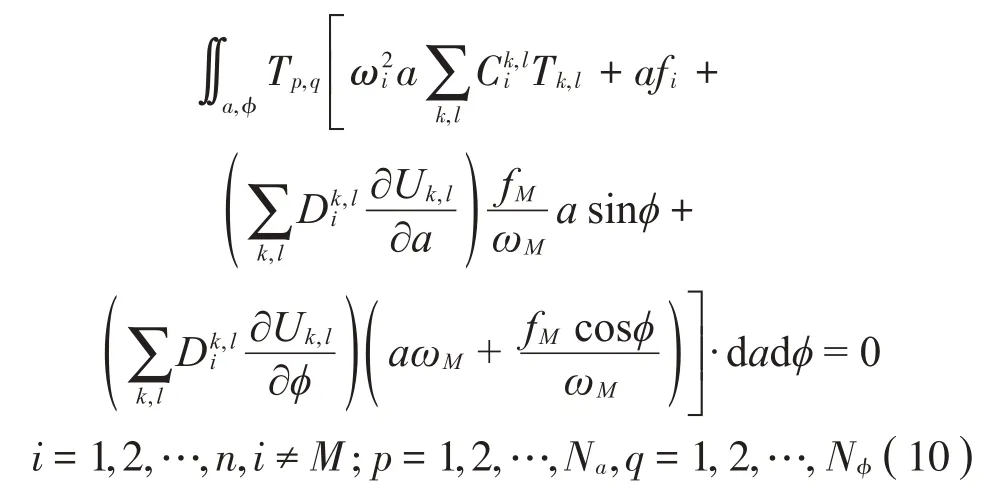
该方程组经过加权积分最终转化为各展开项待求系数C和D的非线性代数方程组，可应用各种数值求根算法如Powell混合算法[17]等求解。而展开式系数代数方程组的形式由对应的非线性模态假设解的形式决定，并将影响后续方程组数值迭代求根过程中Jacobian矩阵的形式。

因为不变流形定义下非线性模态的约束曲面是关于主坐标相角φ在[0,2π] 上的周期连续函数，所以对于T(a,φ)、U(a,φ)关于φ的展开函数可选取一系列谐波函数作为基函数：

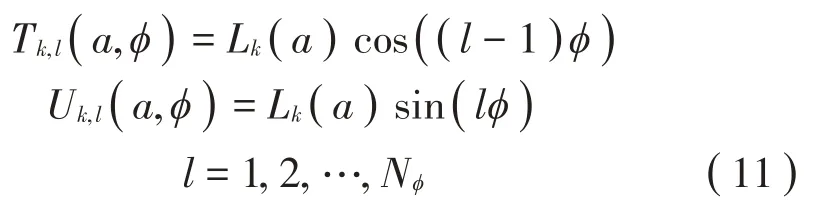
因为在保守系统非线性模态的周期运动中，各自由度的响应均保持同步，所以式(11)中选取余弦函数作为位移响应的展开式基函数，选取正弦函数作为速度响应的展开式基函数[12]。将式(11)代入式(9)、式(10)，得到如下代数方程组：

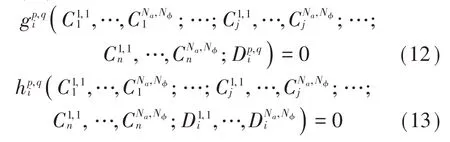
式中：p=1,2,…,Na,q=1,2,…,Nφ;i,j=1,2,…,n,i,j≠M。关于系数C和D的代数方程gp,qi=0和hp,qi=0 分别来自于积分式(9)和式(10)。因方程组(1)中的各非线性刚度项fM和fi(i≠M)耦合了所求的其他位移响应ui，所以式(12)、式(13)中的各代数方程可能含有相应的待求系数C。

2.1 Galerkin分片求解法

根据上述的求解策略，文献[12]提出了一种Galerkin 分片求解法，将不变流形曲面关于主坐标(a,φ)的求解区域沿a方向离散，划分为若干个环状域，分别独立求解各个环状域内的不变流形子曲面。每个环状求解域内，将函数L(a) 假设为线性函数。分别在两个相邻的环域内进行求解，所得的在相接处两个子曲面的函数值一般不同，整体的不变流形曲面会出现阶跃不连续，一般可取相接处的节点在各自求解域中的函数值的均值作为该节点的函数值，以保证解曲面的连续。如图1所示，图1(a)和图1(b)分别为某一不变流形曲面uSub=P(uM,)由原点向外第1、第3、第5个和第2、第4个环状域上求解出的子曲面，各子曲面均在各自子域内独立求解。图1(c)给出了整体不变流形曲面的侧视图，可以看出在相邻曲面的相接处均存在曲面阶跃不连续。图1(d)显示了在各个相邻子曲面相接处函数值取均值后的整体非线性模态曲面，子曲面相接处函数值连续。

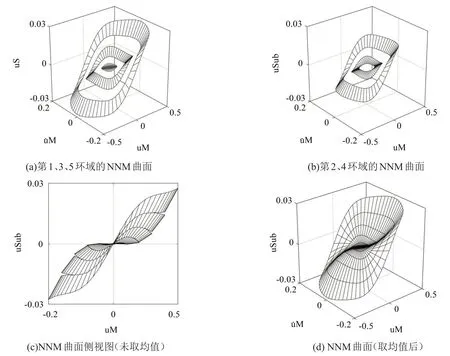
图1 采用分片Galerkin法求解出的非线性模态曲面

若采用更多更细的环状子域分别求解非线性模态曲面，相邻子曲面相接处的阶跃不连续将减小，但合成后的解曲面的精度仍存在不足，在后续算例中将给出说明。

2.2 基于谱单元的Galerkin法

在幅值a维度上采用谱单元进行离散近似。应用Patera提出的谱元法[18]，在将求解域沿a方向划分为相接的各个单元后，在每个单元内采用Lagrange插值函数作为基函数，插值点选择为第二类Chebyshev 多项式在所在单元定义域上对应的各个零点。表1给出了定义域为[-1，1]上第m阶的第二类Chebyshev多项式的零点。

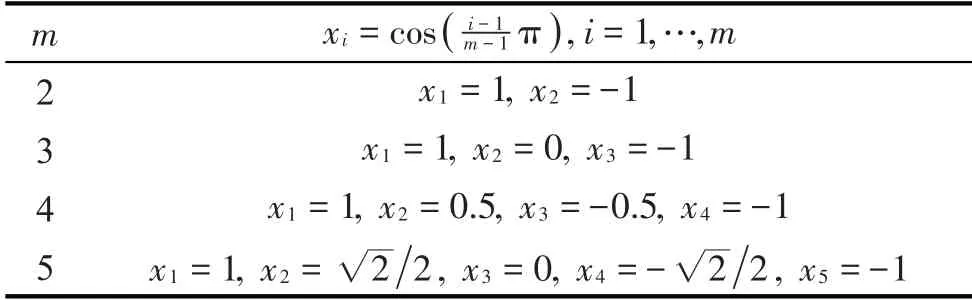
表1 第二类Chebyshev多项式的零点

当L(a) 采用一系列谱单元进行插值近似后，不同于分片法，相邻单元的共用节点处的函数值应相等。图2给出了谱单元上各插值基函数的示意图，设第r个单元具有4 个插值点，第r+1 个单元具有5个插值点，将图中各插值函数结合插值节点的函数值以近似某解曲线。

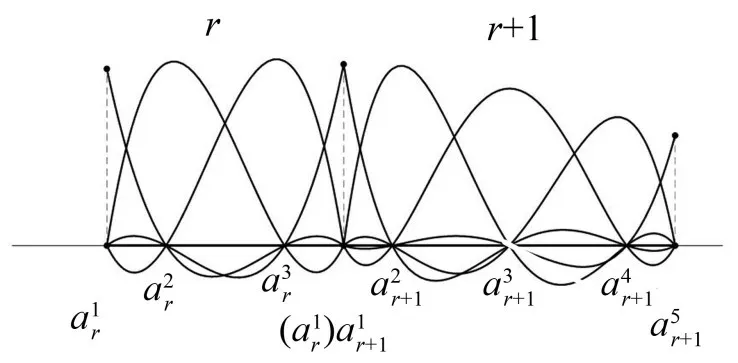
图2 谱单元上的基函数示意图

将[a0,aend] 划分为N个单元，设第r个单元含有包括单元两个端点在内的共mr个节点相邻单元r与单元r+1 的共同节点坐标求解域内共有个插值节点，其中单元内的节点个，单元两端的节点共N+1 个。第r个单元内、除两个端点以外的插值节点函数值对应的基函数分别为：

当r=1,…,N,s=2,…,mr-1

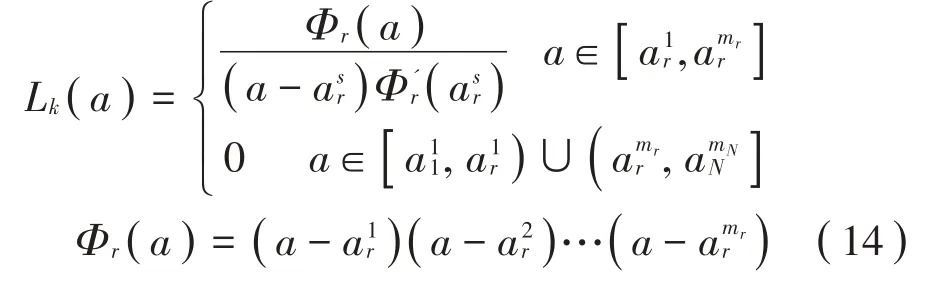
在各个单元的端点，如第r个端点(r=1,…,N+1)，节点函数值对应的基函数分别为：

当r=1时，

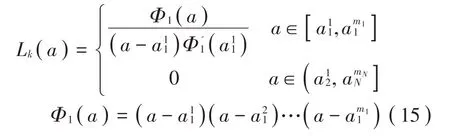
当r=2,…,N时，

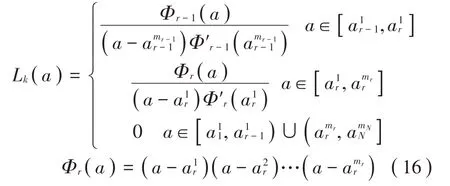
当r=N+1时，

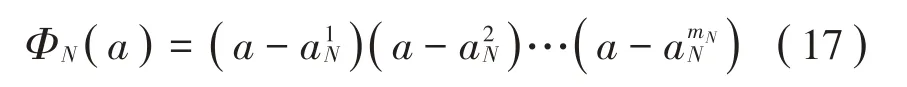
将式(14)至式(17)代入式(11)后再代入式(9)、式(10)，采用Galerkin 法求解。不同于分片Galerkin法，其积分方程的积分域为a方向上两个节点之间的环域，而此方法中每个方程的积分域包含了对应节点的相邻环域，最终得到的代数方程同时考虑了相关邻域内控制方程式(9)式(10)对非线性模态曲面的约束。由于在节点处函数具有连续性，在各个子域上经Galerkin积分获得的有关节点函数值的代数方程之间相互耦合，需联立求解。相比于分片Galerkin 法中求解一系列独立的代数方程组再对节点处函数值取平均的策略，此方法得到的节点值从整体上考虑了每个节点相邻邻域的影响，有可能获得更精确的解，这将在算例研究中进行验证。

后续的非线性代数方程组求根采用基于梯度的迭代数值算法，求解最小二乘意义下方程组的余量函数的最小值。迭代过程中需要计算待求函数的Jacobian 矩阵。采用本方法求解非线性模态曲面展开系数时，其相关的Jacobian 矩阵含有式(18)中的4个分块矩阵。进行数值迭代求根时，矩阵中的函数偏导数采用差分法进行近似。

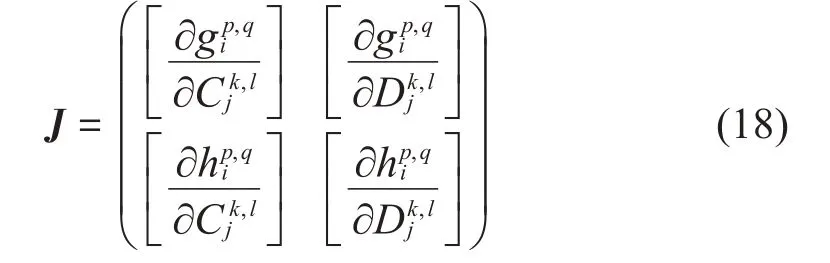
其中：p,k=1,2,…,Na,q,l=1,2,…,Nφ;i,j=1,2,…,n,i,j≠M数值迭代求根中的Jacobian 矩阵将由于在谱单元中选取不同阶数的插值多项式而呈现出其对应特定的稀疏性。设从坐标个数j=1，谐波基函数个数Nφ=2，a方向划分N=2个单元，第一个单元采用3个节点的Lagrange插值多项式，第二个单元采用4个节点的插值多项式。两个单元内的插值节点分别对应第二类Chebyshev多项式的第3阶、第4阶多项式的根。以此为例，图3给出了系数C和D的代数方程组在迭代求根中的Jacobian矩阵结构示意图。

图3中具有阴影底纹的网格表示矩阵中的非零元素。在系数方程组的数值求根迭代过程中，为了简化Jacobian 矩阵的计算，根据其特定的稀疏性只计算矩阵的非零元素。

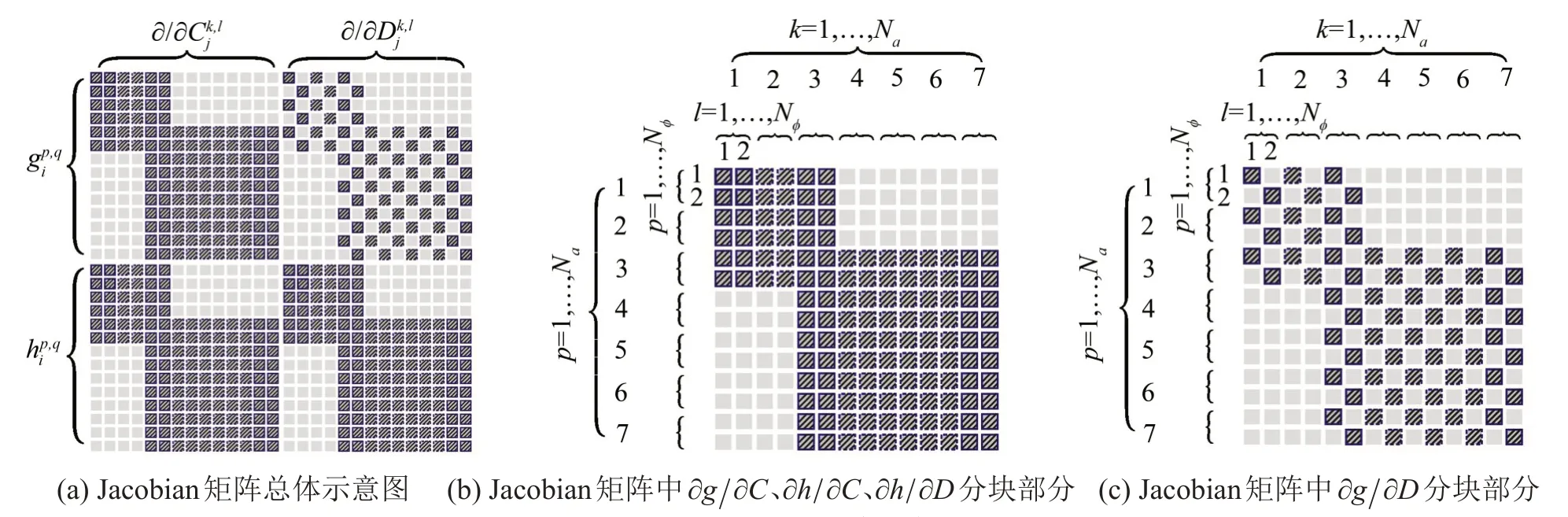
图3 稀疏Jacobian矩阵示意图

3 两种Galerkin方法求解非线性模态的比较

本节以一个具有强二次及三次非线性的两自由度振动系统为例，采用上述的两种方法计算系统所包含的各阶非线性模态，并比较其精确性。

3.1 动力学模型

以文献[15]给出的非线性质量弹簧振动系统为研究对象，如图4所示。集中质量mo可以在u1、u2方向上运动，由两个原长均为L的弹簧连接。沿用文献中采用的Green-Lagrange应变来定义大变形下弹簧的应变：由此推导出的系统动力学方程式(19)中含有二次及三次的光滑非线性刚度项。

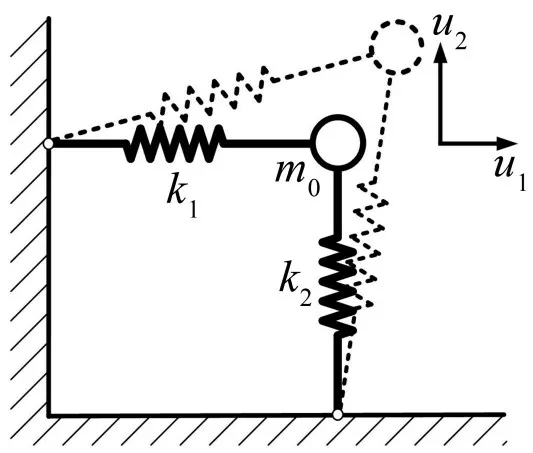
图4 两自由度非线性振动系统示意图

设mo=1kg，L=1m，得到系统的动力学方程。采用文献[15]中的参数设置，考虑k1=1N、k2=2N时的情况。

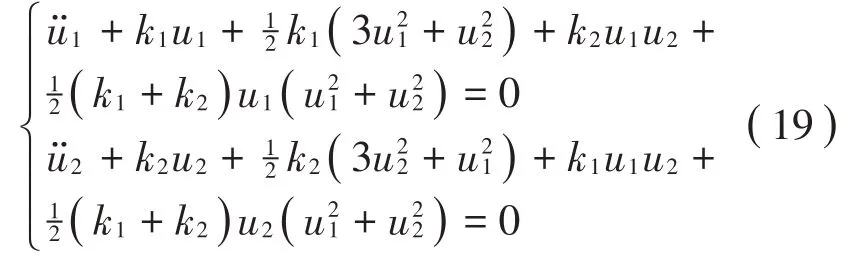
3.2 结果比较

采用以上两类方法求解振动系统(19)的各阶非线性模态。首先应用分片Galerkin 法，将求解域划分为12 个独立子环域，令各子环域a方向的宽度相等，取谐波基函数的个数为6。再应用谱单元Galerkin法求解非线性模态，分别采用了4种网格划分及谱单元阶数的组合，如表2所示。

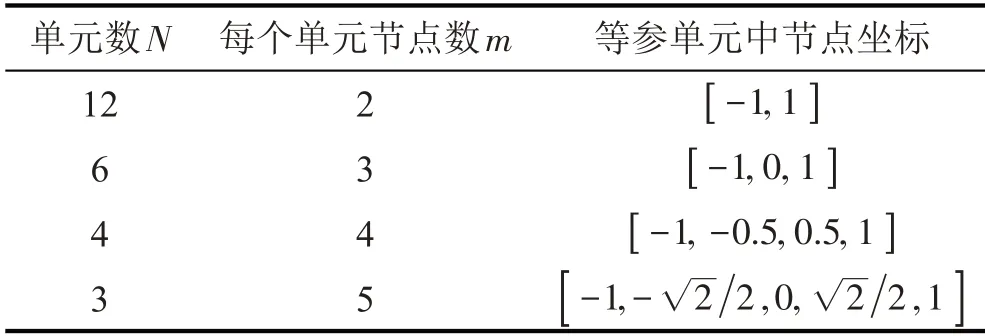
表2 应用谱单元Galerkin法时选取的求解参数

各种组合策略中，设置相邻插值节点间的距离与分片Galerkin 法中独立子环域片数为12 时环域a方向的宽度接近，以比较两类方法在近似的离散程度下所求得的解的精度差异。本例中各种谱单元的组合策略中均令单元的长度相等，取谐波基函数的个数为6。应用两类方法时对所生成的非线性代数方程组进行数值求解，待求系数的迭代初值均取为0，精度取为1×10-6。图5给出了运用两类Galerkin方法求得的第1阶非线性模态的近似曲面。

图5(a)同时给出了发生在系统该阶非线性模态曲面上的一系列周期运动响应，即图中实线所示的一组封闭相轨线。该组周期轨线均通过打靶法进行数值求解得到。取某一初值为(u10,u˙10,u20,u˙20)=(1.7,0,0.009 617,0)的周期响应，代入原方程式(13)，通过Runge-Kutta法进行数值积分，可得参考周期解的时域响应u1(t)和u2(t)。再取另一组初值可得周期解时域响应u1(t)和u2(t)，见图5(b)，以作参考比较。

当采用两类方法分别求得非线性模态曲面近似展开式中的待求系数后，即得到了式(2)形式的非线性模态曲面显式表达式。将其代入方程组(1)中主坐标uM所对应的控制方程中的非线性回复力项，可得关于uM的单自由度的微分方程，方程中只含有uM一个未知函数。取初值对该方程采用Runge-Kutta 法进行数值积分，得到响应解uM(t)。再将该响应序列uM(t)代入式(2)，可得对应发生在非线性模态不变流形曲面上的从坐标响应序列ui(t)。uM(t)和ui(t)描述了非线性模态近似解曲面上的一个响应轨线，因为其是根据近似展开解(2)得出，所以可通过它与对应的参考周期解比较来判断非线性模态近似解的精确性。对于第1阶非线性模态，uM(t)=u1(t)，ui(t)=u2(t)，图5(b)中分别给出了初值为和=(1.9,0)时依据各近似解曲面得出的时域响应。

由图5可以看出，采用各种谱单元的Galerkin法求得的非线性模态曲面，相比于分片Galerkin 法的结果，均具有较高的精度。即使计算幅值较大的非线性模态曲面上的周期轨，根据由谱单元Galerkin法获得的近似解曲面，进而求得的曲面上的周期响应也与参考解较为接近。

图6给出了采用两类方法求解的第2 阶非线性模态的各个解曲面及相应的一组周期轨线，同时给出了初值为= (1.8,0)和=(2.0,0)时依据各近似解曲面得到的时域响应及对应的参考解。采用两类Galerkin方法时选取的参数与求解第1阶非线性模态时选取的相应参数基本相同。系统(19)的第2 阶非线性模态中，u2、为主自由度，u1为从自由度。由图6可以看出，采用一系列谱单元Galerkin 法仍可获得较为准确的第2 阶非线性模态解曲面及其曲面上发生的周期响应。图5(a)和图6(a)同时给出了采用分片Galerkin 法在独立子环域片数为25 时的解。可以看出即使采用了更细的网格，分片Galerkin 法在响应较大区域依然无法获得较为精确的解。

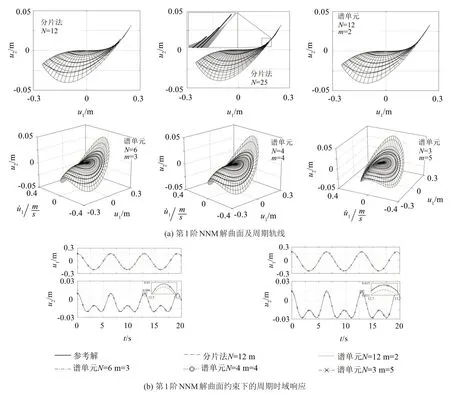
图5 第1阶非线性模态解曲面及其周期响应

图6 第2阶非线性模态解曲面及其周期响应

4 结语

本文采用一种基于谱单元的Galerkin 法，可以较为准确地计算一类无阻尼非线性振动系统在不变流形定义下的非线性模态。相比于已有的非线性模态Galerkin 分片求解法，该方法选取第二类Chebyshev多项式的零点构造每个谱单元的Lagrange插值函数，对求解域进行整体求解。在展开系数的迭代求解中，Jacobian由于谱单元中选取不同阶数的多项式而呈现特定的稀疏性。相较于分片求解法，该方法在求解域较大时仍能获得较为准确的解。