α-块对角占优矩阵与两类迭代法的收敛性

傅河清，蔡 静，高寿兰

(湖州师范学院 理学院, 浙江 湖州 313000)

块对角占优矩阵是具有对角占优特性的分块矩阵.对各种形式的块对角占优矩阵开展性质和迭代法研究，有助于深入了解块矩阵的性质，加快线性方程组的计算速度，降低矩阵的运算规模，使大数据处理更加方便、快捷.目前，很多文献讨论了各类对角占优矩阵的相关性质和对应线性方程组迭代法的收敛性.文献[1]证明了对角占优矩阵的非奇异性，以及当系数矩阵对角占优时，解线性方程组Ax=b的Jacobi迭代法和Guass-Seidel迭代法的收敛性.文献[2]和[3]探讨了线性方程组几种常用迭代法的收敛性条件.文献[4]提出了弱块对角占优矩阵的一个等价定义.文献[5]给出了广义对角占优矩阵的判定条件，指出了广义对角占优矩阵与非奇异H-矩阵的等价性.文献[6]利用 Ostrowski对角占优矩阵给出了非奇异H-矩阵的判定条件.文献[7]～[10]研究了乘幂形式和行列相加形式的α-对角占优矩阵，并确定了这些矩阵的非奇异性，以及Jacobi迭代法、Guass-Seidel迭代法、SOR迭代法和AOR迭代法的收敛性.文献[11]研究了块对角占优矩阵的非奇异性，以及块Jacobi迭代法和块Guass-Seidel迭代法的收敛性.文献[12]探讨了更广泛的α-块对角占优矩阵，得到了等价表征，并拓展了块H-矩阵的判定条件.

本文针对两类块α-对角占优矩阵，证明当线性方程组的系数矩阵为这两类块对角占优矩阵时，块Jacobi迭代法和块Guass-Seidel迭代法均收敛.

考虑分块矩阵：

其中，Akl=(aij)∈Cnknl，k、l=1,2,…,n,对角线上的矩阵为方阵.

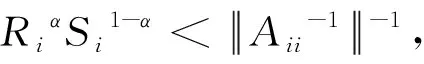
则称A为α-幂乘块对角占优矩阵，记为A∈GD1.

定义2[11]若对任意i=1,2,…,n，存在α∈[0,1],均满足

则称A为α-行列相加块对角占优矩阵，记为A∈GD2.

引理1[12]若A∈GD1，则det(A)≠0.

引理2[1]解线性方程组Ax=b的迭代法x(k+1)=Bx(k)+f收敛，其充分必要条件为:迭代矩阵的谱半径ρ(B)<1.

引理3[12]若A∈GD2，则det(A)≠0.

1 主要结果

定理1若A∈GD1，则解线性方程组Ax=b的Jacobi迭代法收敛.

证明将A分裂如下：

Jacobi迭代矩阵为：

令E为B的同阶单位矩阵,假设ρ(B)≥1,则存在B的某一特征值λ，满足λ|≥1,且

det(λE-B)=det(λE+D-1(L+U))=0，

(1)

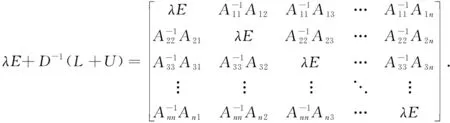
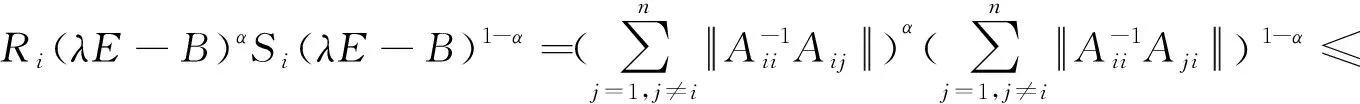
所以，当λE-B∈GD1时，根据引理1得det(λE-B)≠0.这与式(1)矛盾，假设不成立.由此可知，当ρ(B)<1时，解线性方程组Ax=b的Jacobi迭代法收敛.

定理2若A∈GD1，则解线性方程组Ax=b的Guass-Seidel迭代法收敛.

证明将A作同样分裂，则Guass-Seidel迭代矩阵为：

BG=-(D+L)-1U.

假设ρ(BG)≥1,则存在BG的某一特征值λ，满足|λ|≥1，且

det(λE-BG)=det(λE+(D+L)-1U)= det(D+L)-1det(λ(D+L)+U)= det(D+L)-1det(D)det(λ(E+D-1L)+D-1U)=0，

从而易知det(D+L)-1≠0，det(D)≠0.

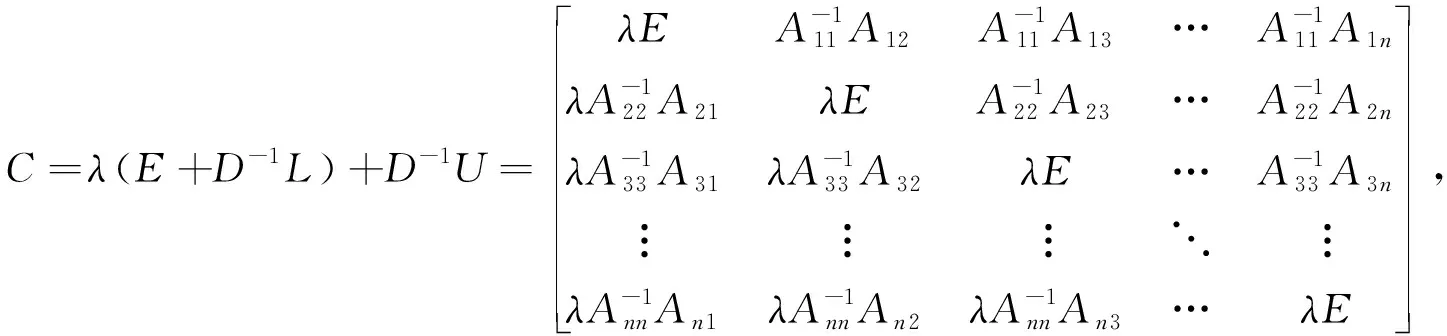
det(C)=0.

(2)

因为，

Ri((λE)-1C)αSi((λE)-1C)1-α=

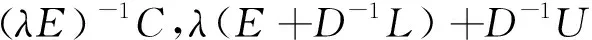
定理3若A∈GD2，则解线性方程组Ax=b的Jacobi迭代法收敛.

证明Jacobi迭代矩阵为：

令E为B同阶单位矩阵，假设ρ(B)≥1,则存在B的某一特征值λ，满足|λ|≥1，且

det(λE-B)=det(λE+D-1(L+U))=0，

(3)

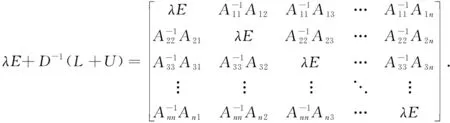
因为，

αRi(λE-B)+(1-α)Si(λE-B)=

所以，当λE-B∈GD2时，根据引理3得det(λE-B)≠0.这与证明中的式(3)矛盾，假设不成立.由此可得，当ρ(B)<1时，解线性方程组Ax=b的Jacobi迭代法收敛.

定理4若A∈GD2，则解线性方程组Ax=b的Guass-Seidel迭代法收敛.

证明迭代矩阵BG=-(D+L)-1U.

假设ρ(BG)≥1,则存在λ为某一特征值，使得|λ|≥1，则有：

det(λE-BG)=det(λE+(D+L)-1U)=

det(D+L)-1det(λ(D+L)+U)=

det(D+L)-1det(D)det(λ(E+D-1L)+D-1U)=0，

从而易知det(D+L)-1≠0，det(D)≠0.

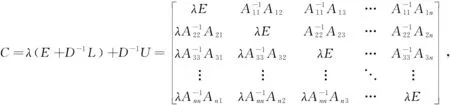
det(C)=0.

(4)

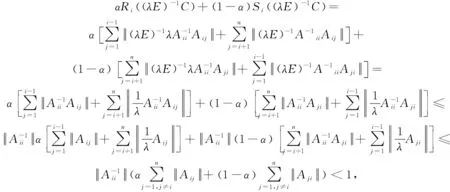
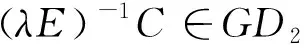
2 结 论

块对角占优矩阵是对角占优矩阵在分块矩阵领域的推广，但与对角占优矩阵相关的迭代法收敛性结果并不能直接推广到块对角占优矩阵.本文在现有成果的基础上，探讨更具有一般性的块α-幂乘块对角占优矩阵和块α-行列相加块对角占优矩阵，证明了这些矩阵对应的块Jacobi迭代法和块Guass-Seidel迭代法的收敛性.这对分块矩阵的研究和应用具有重要意义.