The role of solutes in grain refinement of hypoeutectic magnesium and aluminum alloys
Qingyou Han
Hans Tech,West Lafayette,IN 47906,USA
School of Engineering Technology(Retired),Purdue University,USA
Abstract The effect of solutes on grain formation has been studied over a century but is still under debating,simply because it is a very complex topic.This article focuses on the effect of dissolved solute on the growth,fragmentation of a dendrite and the resultant grain size.Experimental data on grain size in magnesium and aluminum alloys with various solute concentrations are collected and analyzed using phase diagram variables including Q,P,andΔT.The physical meaning of each phase diagram variable is discussed.Curve fitting of the recently proposed two-parameter models with experimental data suggests that there is a clear correlation between the measured grain size and the solidification range of the alloy over the entire range of the hypoeutectic composition.Such a trend of grain size vs.ΔT is closely related to the grain refining mechanisms operating under relevant experimental conditions.A critical review of the grain refining mechanisms indicates that the mechanisms associated with the dendrite fragmentation are operating under the conditions where convection is substantial in the melt during its solidification.
Keywords:Solidification microstructure;Grain refinement;Solute elements.
1.Introduction
This paper deals with the grain formation of the primary dendritic phase during the solidification of a hypoeutectic alloy,in particular,the effect of solute on the grain size of the primary dendritic phase.Here the solute content is defined as the dissolved amount of an element in the molten alloy before the primary dendritic phase precipitates.The content of a solute is not the total content of the element in the alloy.This definition is important in understanding the effect of a solute on the formation of the primary dendritic phase from a molten alloy.
It is well known that two factors make major contributions to the refinement of the dendritic grains of as-cast metals and alloys:(1)suitable insoluble nucleant particles in the melt that nucleate dendritic grains[1–4],and(2)soluble solutes that redistribute during solidification to alter the growth conditions of dendrites[5–9].There is interplay between these two factors.Nucleation has to occur at certain undercooling below the liquidus temperature which is a function of solute content and the potency of nucleating particles.Solutes rejected by the growing solid alter the morphology of the solid-liquid interface which is essential to the survival,growth,fragmentation,and multiplication of the grains.As a result,nucleant particles are capable of producing much smaller grains in alloys containing solutes than in pure metals[10].
The topic of the effect of solutes on grain formation has been studied over a century but is still under debating.The reason is simply because it is a very complex topic.An element added into the melt can affect the grain formation in many ways in addition to alter the growth conditions of dendrites.
First,an element added in the melt may not totally dissolve in the melt.The undissolved part may serve as nucleant particles.As a result,the dissolved amount of the element,i.e.,the content of the solute,is lower than the added amount or the element,i.e.,the element content,of the alloy.The undissolved particles could affect the nucleation and the dissolved among should influence the growth of the dendritic phase.Zirconium is such an element that can affect both the nucleation[11]and the growth[12]of the dendritic phase in a magnesium alloy depending on its status in the melt.Research on the survival of Zr particles in molten magnesium alloys is scarce.
Second,an added element that is totally dissolved in the melt may form compounds with the elements in the alloy or oxygen in the atmosphere prior to the precipitation of the dendritic phase.Typical examples include elements that have peritectic reactions with the solvent element,such as titanium in aluminum[3,10]or zirconium in magnesium[13].Intermetallics formed during peritectic reactions prior to the formation of the dendritic phase could be potent nucleant particles that are very effective in the grain refinement of the dendritic phase[10].This phenomenon is well known but when it comes to the effect of an element in a multicomponent alloy system,the phase diagrams become unreliable so the peritectic reactions are usually ignored.The formation of compounds prior to the precipitation of the primary dendritic phase also consumes the elements and makes its solute content(dissolved amount)and thus its efficacy on the growth of dendrites reduced.
Third,a dissolved element may interact with the existing solid particles in the melt,modifying the surface properties of the particles and improving their nucleation potency.Little attention has been paid on such an effect in the literature on grain formation in aluminum or magnesium alloys.However,in the field of powder metallurgy,it is well known that an addition of a trace amount of titanium significantly reduces the contact angle between ceramic particles(oxides,nitrides,borides,carbides,aluminides and etc.)and molten aluminum[14–16].Such a phenomenon can be interpreted as improving the nucleation potency of these ceramic particles for the primary dendritic phase in molten alloys.Modern AlTiB grain refiners for aluminum alloys usually contain an excess amount of titanium,i.e.,the atomic ratio of Ti/B is higher than 1/2,to ensure their efficacy in grain refinement.
Fourth,the dissolved solutes in the melt interact with each other during the diffusion process by altering their diffusion coefficients[17,18].The growth of a dendrite is a diffusioncontrolled process.Elements that tend to form intermetallic phases in the eutectic reaction usually pose strong chemical affinity with each other.The formation of the eutectic phases should not affect the grain size if these phases are formed at fraction solids higher the dendritic coherency point.However,the chemical affinity among these elements is bound to affect their diffusion coefficients.Unfortunately,accurate measurements of diffusion coefficients in the liquids are scarce[19].

Fig.1.Trends of grain size,D,vs.bulk solute composition,C0,in hypoeutectic Mg-Al alloys.
To fully understand the effect of solutes on grain formation in an alloy,one has to examine a complete series of events leading to the formation of the final grains,including,but is not limited to,the nucleation of pre-dendritic particles(embryos or baby dendrites),the fragmentation of dendrites,the transportation of these crystals into the bulk liquid,the survival and multiplication of the crystals in melt of certain superheats,growth,multiplication and settling in the mushy zone.Different alloys and different casting conditions should have different results on grain refinement.Unfortunately,work that covers all these events on grain formation is scarce.As a result,results reported in literature are not in good agreement.
The purpose of this paper is to examine the basic effect of solute content on grain size in simple binary hypoeutectic alloys,where there are no interactions among alloying elements and no intermetallic phases that form prior to the precipitation of the primary dendritic phase.Data from well-controlled experiments to minimize the effect of superheat are used to illustrate the basic relationship between grain size and the solute content and the relevant phase diagram of the alloy system.The grain size is then plotted against phase diagram variables to depict simple mathematical equations that fit experimental data.The dependence of grain size on the phase diagram variables obtained from experimental data is analyzed to reveal the operating mechanisms of grain refinement under various solidification conditions.
2.Grain size and phase diagram
Fig.1 depicts the relationship between grain size and solute(aluminum)content,C0,within the solubility limit,CSL=11.5 wt.%,in the primary magnesium phase in hypoeutectic Mg-Al alloys[20,21].The results were obtained by pouring the molten alloys at a given temperature so the superheat for each alloy varied with aluminum contents.Generally,the measured grain size decreases monotonously with composition for alloys of various purity as shown in Fig.1.Such a trend has also been reported in Mg-Zn,Mg-Si,Mg-Ca and Mg-Zr alloys when the composition ranges of the alloy is within the solubility limit,CSL,of the phase diagram[22–24].However,no results from well controlled experiments have been found in the literature with the grain size measured for a magnesium alloy system with its composition beyondCSL.In fact,limited work is available on the measurement of grain size over the entire composition range of other hypoeutectic alloys as well[25–27].

Fig.2.Phase diagram of Al-Cu hypoeutectic alloys(a)and the relationship between grain size and solute composition(b)in the composition range of 0
Fig.2 illustrates the relationship between grain size and composition with respect to its phase diagram over majority of the hypoeutectic compositions for the hypoeutectic Al-Cu alloys[25].Similar diagrams can also be drawn for the Al-Si and Pb-Sb alloys[26,27].The general trend is that grain size reaches minimum at compositions nearCSL.Maxima in grain size occur at pure metal whereC0=0 or near the eutectic compositions,CE.There is a“U”type of relationship between grain size and composition with its minimum near the solubility limit,CSL,of an alloy system where the solidification interval,ΔT,is the greatest.Such a“U”type relationship with respect to composition has not been well described in literature yet but are found at least in Al-Si and in Pb-Sb alloys as well[26,27].
The experimental data on Al-Cu alloys shown in Fig.2 is an excellent example because pure metals were used to eliminate the effect of residual grain refiners on grain size and the ingots for grain size measurement were poured at a given superheat in molds held at a given temperature difference to the solidus of the alloy[25].In fact,it is the only experiment in the literature that the superheat and cooling rates were controlled.The minimum in grain size occurs near the solubility limit of copper in the primary aluminum phase.Such a“U”shaped relationship between grain size and alloy composition is a native effect of the solute on grain refinement during the solidification of the molten alloy.The“U”shaped relationship in Al-Cu alloys was confirmed by other researchers in experiments where the superheat varied slightly when the metal was poured[28].The“U”shaped relationship was not supported in experiments where(1)the superheat was not controlled,(2)the melt was solidified the crucible within which it was melt,meaning no pouring,and melt in the crucible was cooled in air with low cooling rates[29].Convection within such a crucible would be very limited and slow cooling would provide much times for solute depleted dendrites to float out of the mushy zone since the dendrites are actually lighter than the bulk melt when the copper content is high.
3.Phase diagram variables
In evaluating the effect of solutes on grain refinement,a number of phase diagram variables containing solute concentration have been proposed[6–9].Generally,these variables can be categorized into two types:a constitutional supercooling(CS)parameter,P,in the form of[17,31–33]:

and a growth restriction factor,Q,in the form of[6,8,26,34]:

whereC0is the bulk concentration of a binary alloy,mis the liquidus slope atC0,andkis the equilibrium partition coefficient.PandQare related withkasQ=kPfor binary alloys.Oftenmandkare considered as constants,implying that the solidus and liquidus are straight lines which is probably true for diluted alloys withC0smaller than the solubility limitCSL.Table 1 lists thekandmvalues for some of the alloy systems.For diluted alloys withC0≤CSL[25],

Table 1Phase diagram data for selected binary alloys.

Eq.(3)means thatPequals the solidification range,ΔT,of the alloy with the solute content ofC0andQequals the solidification range of an alloy with the solute content ofkC0.For binary alloys,Pis considered to be proportional to the constitutional supercooling at the front of an advancing solidliquid interface,andQis inversely proportional to the growth rate at the tip of a growing dendrite[11,22].
For multi-component alloys,PandQcannot be simply related usingk.Assuming that the diffusion coefficients of the solute elements are equal and there is no interaction among solutes on their diffusion coefficients,P,is derived as[17]:

whereNis the total number of solutes,andidenotes the parameters of theith solute in the alloy.Without mathematicaljustifications,Qis assumed as[30]:
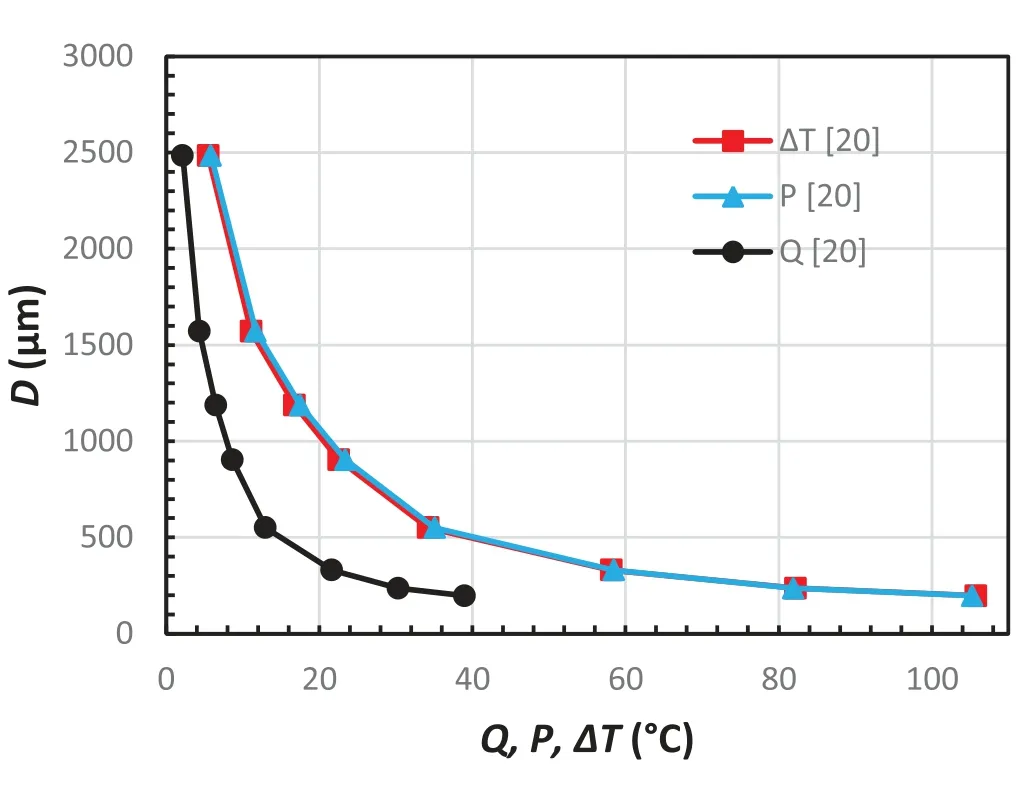
Fig.3.Relationship between grain size,D,and phase diagram variables,Q,P,andΔT,in hypoeutectic Mg-Al alloys with C0>0 and C0 The phase diagram variables,PandQ,were initially used to present grain size as a function of a number of variables such ask,m,C0in a 2-D diagram for wrought alloys(C0≤CSL)[17,30–34].There are nice monotonous relationships between grain size and the phase diagram variables.Simple empirical models were then proposed to correlate grain size with phase diagram parameters.A widely used model is in the form[34]: whereAandBare two constants/parameter which are affected by the addition of grain refiners and by the cooling conditions of the solidifying alloy.ZisQ,PorΔT.Eq.(6)fits experimental data reasonably well in wrought alloys except for whenZorC0approaches zero. Fig.3 illustrates the relationship between grain size andQ,PandΔTfor magnesium-aluminum alloys in the composition range ofC0 Fig.4.Relationship between grain size,D,and phase diagram variables,Q,P,andΔT,in hypoeutectic Al-Cu alloys with 0 However,when plotting the grain size againstPorQover the composition range containingCSL,i.e.,C0varies from zero to greater thanCSL,the curves become“U”shaped as reported in Refs[12,25,30]..In fact,any curve shown in Fig.2 should be“U”shaped if the grain size is plotted againstPorQdefined by Eqs.(1)and(2)although such experimental data are unavailable in Mg alloys. Fig.4 illustrates the“U”shaped curves ofDvs.QandDvs.Pin Al-Cu alloys.Grain size,similar to Fig.3,decreases with increasingQorPwhenC0 Still,there is a monotonous relationship between grain size and the solidification range,ΔT,of the alloy as shown in Fig.4.The“U”shaped relationship betweenDand phase diagram variables,QorP,results from the breakdown ofP=ΔTwhenC0>CSL.Before discussing the breakdown ofP=ΔTwhenC0>CSL,let’s first explore the physical meanings ofQandP. Fig.5.A schematic illustration of the temperature and composition profiles when the solid is growing at a constant rate,R,with a planar solid-liquid front under a constant temperature gradient. Fig.5 illustrates the composition profiles,CSxfor the solid andCLxfor the liquid,and the resultant liquidus profiles,TEx,when the solid grows from the left of the sample to the right at a constant growth rate ofRunder a constant temperature gradientG.The composition of the first layer of solid forming from the liquid iskC0,and the corresponding liquidus and solidus of this solid layer areTL+mC0(k-1)andTL,respectively[35],whereTLis also the liquidus of the alloy ofC0.Although the solidification range of the alloy ofkC0ismC0(k-1)which isQ,it is important to note that the liquidus of the alloy ofkC0is higher than the liquidus of the alloy ofC0byQ.On the other hand,the amount of solute which is entrapped into the first layer of the solid iskC0and the amount of solute which is rejected to the liquid due to the formation of this first solid isC0(1-k).Part of this amount of rejected solute would segregate at the solid-liquid interface,causing a depression of the interface temperature proportional but not equal tomC0(k-1)orQ.Therefore,Qis the solidification range of the alloy ofkC0,is the increase of liquidus in respect to that of the alloy ofC0,and is proportional to the temperature depression at the solid-liquid interface when the first layer of solid precipitates from the liquid of the alloy ofC0where 0 As the solid grows from the left side of sample towards the liquid,the composition in the solid,CSx,increases fromkC0towardsC0and the corresponding liquidus decreases fromTL+QtowardsTLwhere the growth reaches its steadystate conditions.Under such conditions,the compositions in the solid and in the liquid on the solid-liquid interface are shown in Fig.5 asC*SandC*L,respectively,whereC*S=C0,=C0/kwhenC0 and i.e.Pequals the solidification range of the alloy whenC0 Problems arise whenC0>CSLEqs.(7).and(8)break down becauseC0/kbecomes greater thanCEifkandmare still assumed constants.Physically,the peak concentration,C*L,should always be smaller or at most equal toCEotherwise the eutectic phases would form at the freezing front.The use ofC*L=C0/kwould overestimate the peak concentration value and thus thePvalue(not theQvalue)which leads to the formation of the“U”shaped curve when plottingDagainstPas shown in Fig.4.However,theDvs.ΔTcurve shown in Fig.4 is still monotonous,indicating that there is a good relationship between grain size and the solidification range of an alloy. One way to correct the overestimate ofPdue toC0/k>CEis to define an equivalent distribution coefficientk*as[25,38]: Substituting Eqs.(9)and(10)into Eqs.(7),and(8)yields: Substituting Eqs.(9)and(10)into Eqs.(1)and(2),respectively,yields modifiedQ*andP*in the form: and Fig.6.Relationship between grain size,D,and the modified phase diagram variables,Q,P,andΔT,in hypoeutectic Al-Cu alloys with 0 It can be easily proven from a phase diagram that are valid over the entire range of the hypoeutectic composition in a binary alloy system,i.e.,P*=ΔTandQ*=k*ΔT. Fig.6 depicts the relationship between grain size and the modified phase diagram variables using data from Fig.4.TheDvs.P*data almost overlap with theDvs.ΔTdata.TheDvs.Q*relationship is also monotonous but clearly the slope for the lowQ*alloys are different to that of the highQ*alloys because the solidus front in lowQ*alloys rejects solute while the eutectic front in highQ*alloys does not reject solute in its growth direction[38],which affect the morphology of the dendritic freezing front. Two-parameter models that can be used for correlating grain size to phase diagram variables shown in Figs.4 and 6 include[38]: and AtZ=0,Dis a function ofAand has a certain value.One of the characteristics of Eqs.(15)and(16)is that they can be transformed to linear relationships in the forms of: and These linear equations offer a simple way to test the applicability of the models to the grain size data and to calculate their parameters,AandB,by linear regression. Table 2 summarizes the results of curve fitting of Eqs.(6),(15)and(16)with experimental data in alloys which exhibit minimum interactions between solutes and grain refiners.The solubility limit,CSL,of a binary alloy is listed in the second column.Z,is listed only asQorΔTsinceP=ΔTwhenC0≤CSL,P*=ΔT,andQ*=k*ΔT.The parameter values associatedΔTis highlighted for an easy comparison with that associated withQ.When fitting Eq.(6)with experimental data,data atZ=0 are removed because the equation is not valid atZ=0.TheR2value for each linear equation is boldfaced to show the linearity of the equation. WhenC0≤CSLandC0is much greater than zero,for example in Mg-Al alloys[20,21],theR2values in Table 2 are greater than 0.88,indicating a fairly good curve fitting quality using either one of these three equations. For alloys whereC0≤CSLandC0approaches zero,for example the Al-X alloys in Table 2,theR2value associated with Eq.(6)is much smaller than that with Eq.(15)or Eq.(16),especially in Al-X without the addition of grain refiners(Al-5Ti-1B). Fig.7 shows the results of curve fitting using Eq.(15)to the experimental data of Al-X alloys[33].The black squares are the data points in binary alloys without the addition of grainer refiners and the red dots are the data points for in binary alloys grain refined using Al-5Ti-1B and at an addition level of 0.01Ti.TheR2values are not very high but large data scatters mainly occurred for alloys with very smallΔTorQvalues,i.e.,very smallC0values.This is understandable because it is difficult to measure the size of large grains accurately for these alloys with very smallΔTorQvalues.Still,it is evident that the quality of the curve fitting forDvs.ΔTis better than that forDvs.Q(see theR2values in Table 2). Table 2A,B,and R2 values obtained by fitting Eqs.(6),(15)and(16)to experimental data in various alloy systems[33,25]. The quality of curve fitting using Eq.(6)is generally much less satisfactory than that using Eq.(15)or Eq.(16).The differences in theR2values of these two-parameter models are much greater in alloys without the addition of grain refiners than that with the addition of grain refiners.Fig.8 illustrates the curve fitting results using Eq.(6)and experimental results in Al-X alloys[33].It can be seen clearly that the main issues are associated with data at either large or small values ofQ.WhenQapproaches 0(or 1/Qapproaches infinity),the measured grain size still has certain values so theDvs.1/Qcurve should approach a plateau,which is the grain size of pure metal.This means that the slope,B,could be 0 should experimental data be taken in the regions ofQ<0.2(1/Q>5).On the other hand,the slope,B,could be very large should experimental data be taken in the regions ofQ>0.2(1/Q<5).Thus,theBvalues obtained from experimental data are extremely sensitive to the range ofQvalues of the alloys.Such large data scatters in theDvs.1/Qcurves at both small and largeQvalues are understandable because 1)the inherence mathematic issue with 1/Qat smallQusing Eqs.(6),and(2)the“U”shaped nature of the curve at largeQas shown in Figs.2 and 4.Although the latter can be resolved using the modified phase diagram parametersQ*orP*to replaceQorP,Eq.(6)should not be used in alloys of extremelysmallZ(Q,P,orΔT)values,i.e.,alloys withC0approaches zero. Fig.7.Curve fitting of Eq.(15)to experimental data in binary aluminum wrought alloys[33].(a)lnD vs.ΔT,and(b)lnD vs.Q. Fig.8.Curve fitting of Eq.(6)to experimental data on grain size,D,in binary aluminum wrought alloys[33]. For alloys where 0≤C0≤CEandCE>CSL,for example in Al-Cu alloys[25,28],theR2values associated withΔTare much higher than that withQ,suggesting that the twoparameter models usingΔTfit experimental data much better than that usingQ.For such alloys which exhibit“U”shaped relationship betweenDandPorQas shown in Fig.4,ΔT(P*,orQ*which can be related toΔT)has to be used to correlate the two-parameter models with experimental data. Experimental data given in Table 2 generally manifest themselves thatΔT(orP)is better parameter to relate grain size using the two-parameter models thanQ.In fact,such a conclusion has been made by researchers themselves who performed these well controlled experiments on the effect of alloy compositions on grain size in alloys[17,18,25,28,31,33].The reason thatΔTis better related to grain refinement data thanQhas to be understood by considering the mechanisms of grain refinement under the influence of the solute in alloys. Mechanisms that are operating for a solute element for grain refinement of alloys have been well described.These mechanisms include constitutional supercooling[42],free chill crystal formation[40],dendrite arm remelting[39],grain separation from the mold surface[41],which is also related to dendrite arm remelting,and others such as crystal showing from the surface[43]. The constitutional supercooling theory[42]is based on the idea that equiaxed grains nucleate in the liquid ahead of the growing solid-liquid interface.Solute rejected by the growing grains diffuses away from the solid-liquid interface,forms a concentration gradient and a resultant liquidus temperature gradient ahead of the freezing front.The liquid ahead of the growing front can become constitutionally undercooled as shown in Fig.5.When the constitutional supercooling is greater than the nucleation undercooling associated with the foreign particles in the liquid,heterogeneous nucleation occurs.Thus grain formation is controlled by a wave of nucleation events preceding the solidification front.At given cooling conditions and the number density of nucleant particles,the grain size decreases with increasingQbecause the growth rates of dendrite decreases with increasingQ[6]. The constitutional supercooling mechanism has been widely used for correlating grain size toQ[8,34]in the past two decades probably because it is relatively easy to model.The mechanism has been supported by experiments carried out in thin slice specimens directionally solidified horizontally where the alloy is meltedin-situand convection in the melt is suppressed[44].However,as pointed out by Chalmers himself[40],such a mechanism should only be used under conditions where convection is minimized.The mechanism probably also works in small ingots of a dilute alloy meltedin-situin a crucible and cooled in air slowly so that convection can be minimized[29],although the crystal showing mechanism may also work under such conditions. Still,fragmentation and floating of the fragments in metallic alloys have been observed in vertically solidified thin slice specimens using X-ray radiography in Al-Cu alloys[45,46].This is also one of the reasons that experimental results from Ref[29].are not used in this study.These fragments would prevent new grains from nucleating ahead of the freezing front since the nucleation undercooling is greater than the growth undercooling of the fragments.Even though new grains are nucleated,the curvature undercooling of these newly formed nuclei or embryos is still much greater than that of the fragments.As a result,these new grain embryos cannot survive in the melt due to Ostwald ripening,and the constitutional supercooling mechanism should be discounted when dendrite fragments exist and survive at the freezing front. When convection in the melt is substantial such as during gravity casting,the dendrite remelting mechanism[39]should be the dominant mechanism operating for the grain refinement in alloys,especially when grain refiners are added in the melt so a large amount of free chill crystals can be formed[40].The dendrite remelting mechanism suggests that secondary dendrite arms grow with a necked shape,due to solute build up near their base.When there is an increase in local temperature,the secondary dendrite arms tend to be remelted at the necks,forming detachments.Necking can also be formed near the mold wall on the in grains formed on the mold surface so the entire branch of the grain can be remelted and separated from the mold surface[41].Detachment of the arms can also occur due to Ostwald ripening,forming fragments.These fragments can be brought to the melt ahead of the freezing front and grow into new dendrites.The solidification interval of an alloy,ΔT,and the phase diagram variablePare closely related to the dendrite arm remelting mechanism since(1)Pis the temperature depression of the soli-liquid interface which can be related to the neck formation at the dendrite base,and(2)at a given temperature gradient,ΔTwhich equalsP*is proportional to the depth of the mushy zone and the number of secondary dendrite arms which are the sources of new grains when dendrite fragmentation occurs.The greater the value ofΔT,the greater the number of secondary dendrite arms which form the dendritic fragments.As a result,the grain size decreases with increasingΔT.Furthermore,the growth rate of a dendrite,which is inversely proportional toQ,is also included in thePorΔTsinceP=ΔT=Q/kforC0≤CSLandP*=ΔT=Q*/k*for 0≤C0≤CEandCE>CSL.The growth rate of a dendrite also decreases with increasingP,P*orΔT,leading to the formation of smaller grains. Experimental validation of the dendrite remelting mechanism can be found in thin slice specimen[45,46]as well as in ingots poured under gravity casting processes including direct chill castings[36,47–51],in castings made through forced mold filling processes such as high pressure die casting[52],and in samples solidified under forced flow conditions using external stirring[53–54]or external fields[55–57]. Convection in thin slice specimens is restricted by the mold surface,creating an ideal environment for studying diffusion controlled solidification phenomena in a quiescent melt of metals and alloys.Still coarsening caused dendrite fragmentation has been observed in metallic alloys by serial sectioning[58]and by using X-ray radiography[59,60].Using synchrotron X-ray video microscopy to observe dendrite fragmentation in vertically grown Al-20%Cu alloy,Mathiesen et al[59].found that dendritic fragments floated ahead of the freezing front because the solid fragment is lighter than the bulk liquid.Zimmermann et al[60].performed similar experiments in Al-10%Cu alloy to observe dendrite fragmentation.They found that the fragmented particles could be entrapped by the freezing front when the front grew faster than the floating rate of the particle.Fragments or even branches of dendrite can be transported out of the mushy zone when bubbles burst in thin slice specimen during directional solidification[61].The existence of the floating fragments ahead of the freezing front would certainly eliminate the formation of new grains by nucleation.Even new grains do nucleate ahead of the dendritic front,these small nuclei should not survive near the much large fragments due to the Ostwald ripening process.Thus the final grain size in such specimens should be controlled by the dendrite remelting mechanism. When convection is substantial during gravity casting,dendrite fragmentation and the transport of the fragment out of the freezing front is much easier. The direct-chill casting is the most quiescent metal casting process where the maximum flow speeds in the sump is only a few millimeters per second[48,62,63].Floating grains,or daisies,white,isothermal dendrites,were reported as early as 1948 by Dobatkin[64].Their appearance has been described by several researchers as coarse dendrites of relatively pure metal[47–51].Their size can be as large as 300 μm[3].As much as over 68% of the grains in the center of an DC cast ingot comprises of floating grains[65].These floating grains,either free chill crystals[4]or dendrite fragments,are detached from the chill zone of the solid shell formed near the top of the crater and transported downstream[47].Numerical modeling suggests that these floating grains are transported throughout the sump in the solidifying ingots[48,62,63].In fact,the floating grains can even survive for certain amount of times in the melt at temperatures slightly higher than the liquidus temperature of the alloy[35,66].The existence of the floating fragments in the sump ahead of the freezing front would certainly eliminate the formation of new grains by nucleation.Thus the final grain size in such specimens should be controlled by the dendrite remelting mechanism[39]. For other gravity casting processes where hot metal is poured into a cold mold,the flow rates during pouring or mold filling are a few orders of magnitude greater than that during DC casting.As a result,fragmentation is much severe.As demonstrated by Ohno et al[41].,separation of an entire dendrite branch from the mold wall occurs,let alone the remelting of secondary dendrite arms[39].As a result,there are ample fragments/floating grains in the melt that would eliminate the possibility of forming nucleating new grains ahead of the freezing front.Indeed,as pointed out by Chalmers and his co-workers[67],no new grains are nucleated at any time after pouring and the mechanism of constitutional supercooling is not the operating mechanism for grain refinement in these gravity casting processes,especially when the superheat is low which is favor in industrial practice in order to reduce defects in castings.A detailed thermal analysis in metallic alloy indicated that no new grains were nucleated at any time after pouring,ruling out the mechanism of constitutional supercooling in grain refinement in gravity castings[67,68].Data from samples for curve fitting of this study were in fact obtained under such conditions.This is the reason that grain size in those samples correlated better withΔTthan that withQas shown in Table 2 and Figs.7,8. It is important to note that the grain size vs.Qrelationship,which works better under conditions of no convection in the melt,should not be extended to solidification conditions where convection in the melt is extremely vigorous so dendrite fragmentation is the dominant operating mechanisms for grain refinement.Such conditions include high pressure die casting,solidification under external stirring or under the influence of external fields.In die casting process,fragments,termed as externally solidified dendrites(ESDs),form in the shot sleeve and spread across the entire casting when the melt is injected from the shot sleeve to the casting cavity.The amount of ESDs formed in the shot sleeve can be so great that they can choke the mold filling at the in-gate during die casting process[52].Mechanical stirring used for semi-solid processing is another example of using dendritic fragmentation for obtaining spherical primary phase[53,54].External fields have been used for grain refinement in alloys without the need of using chemical grain refiners[55]. Grain size varies inversely with the solidification range of the alloy in a binary alloy system.Of the Phase diagram variablesQ,P,andΔT,the dependence of grain size onΔTorPis better than onQ.Such a dependence of grain size onΔTsuggests that the dominant mechanisms operating on the effect of solute on grain refinement are related to dendrite remelting,fragmentation and multiplication when substantial convection exists in the liquid during alloy solidification.This is becauseΔTorPis a measure of the depth of the mushy zone at a given temperature gradient and represents the number of secondary dendrite arms that have the potential of forming dendritic fragments under the influence of convection.The greater the value ofΔTorP,the greater the number of secondary dendrite arms and the smaller the resultant grain size under a given solidification conditions.These fragments formed from the detached secondary dendrite arms are the sources of new grains ahead of the freezing front. Of the three two-parameter models proposed in the literature,the following two parameter models, and can be used for predicting grain size atΔT=0.These two models fit experimental data better than those using 1/Q,especially when theQ(orΔT)values are small. Declaration of Competing Interest The authors declare that they have no known competing financial interests of personal relationships that could have appeared to influence the work reported in this paper. Acknowledgments The author is indebted to Dr.Shuanglin Chen of CompuTherm,LLC for providing the solidification range data for the aluminum alloys.The author also thank Miss.H.Han for reviewing and editing the manuscript.



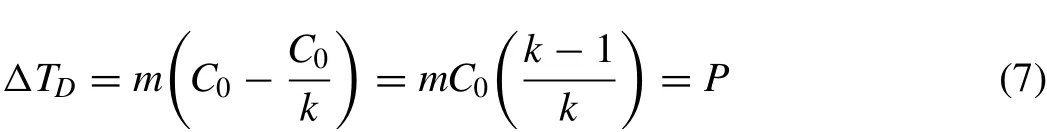


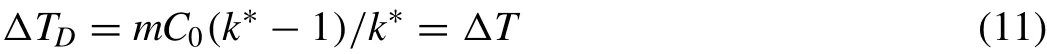




4.Models correlating grain size with phase diagram variables







5.Mechanisms of grain refinemen
6.Conclusions


 Journal of Magnesium and Alloys2022年7期
Journal of Magnesium and Alloys2022年7期
