三面骰子的动力学分析和几何特性
范祥彬,卢奕合,刘逍娜,王铁成
(山西大学 物理电子工程学院,山西 太原 030006)
2022年CUPT第7题:硬币落地时侧面站立的情况十分罕见.为了使圆柱形骰子落下时立在侧面、正面与反面概率相同,应该具有怎样的物理性质和几何特征?
目前已经有研究者对三面骰子的问题展开过详细的描述[1],但是仍然存在一些细节没有得到解答.例如,在投掷三面骰子时,如果给予它水平方向的速度,侧面出现的概率会发生什么变化? 三面骰子反复弹跳是否会有不同的结果?基于以上问题,本文进行了相关研究和讨论.
首先,把硬币定义为圆柱体,当它充分翻转落地时,虽然侧面出现的概率极小,但却不能忽略其可能性.硬币除了有1个平移自由度外,还有2个旋状自由度,但是在实际情况下,由于硬币的对称性(侧面高度趋于零),平移自由度作用并不明显,因此可以认为理想硬币落在正面或者反面的概率近似为1/2,但是一旦改变其侧面的厚度,立在侧面的概率就会改变,正面或者反面的概率将不再是1/2.
对于硬币、正方体骰子和陀螺骰子而言,立在不同面的概率可以通过物体的对称性来预测.但当物体不再具有精确的对称性时,立在不同面的概率就不可能只受几何特征的影响,还需要考虑弹跳的影响.
1 三面骰子的定义
三面骰子的立体图及截面图如图1所示,设圆柱半径R与高度h的比为
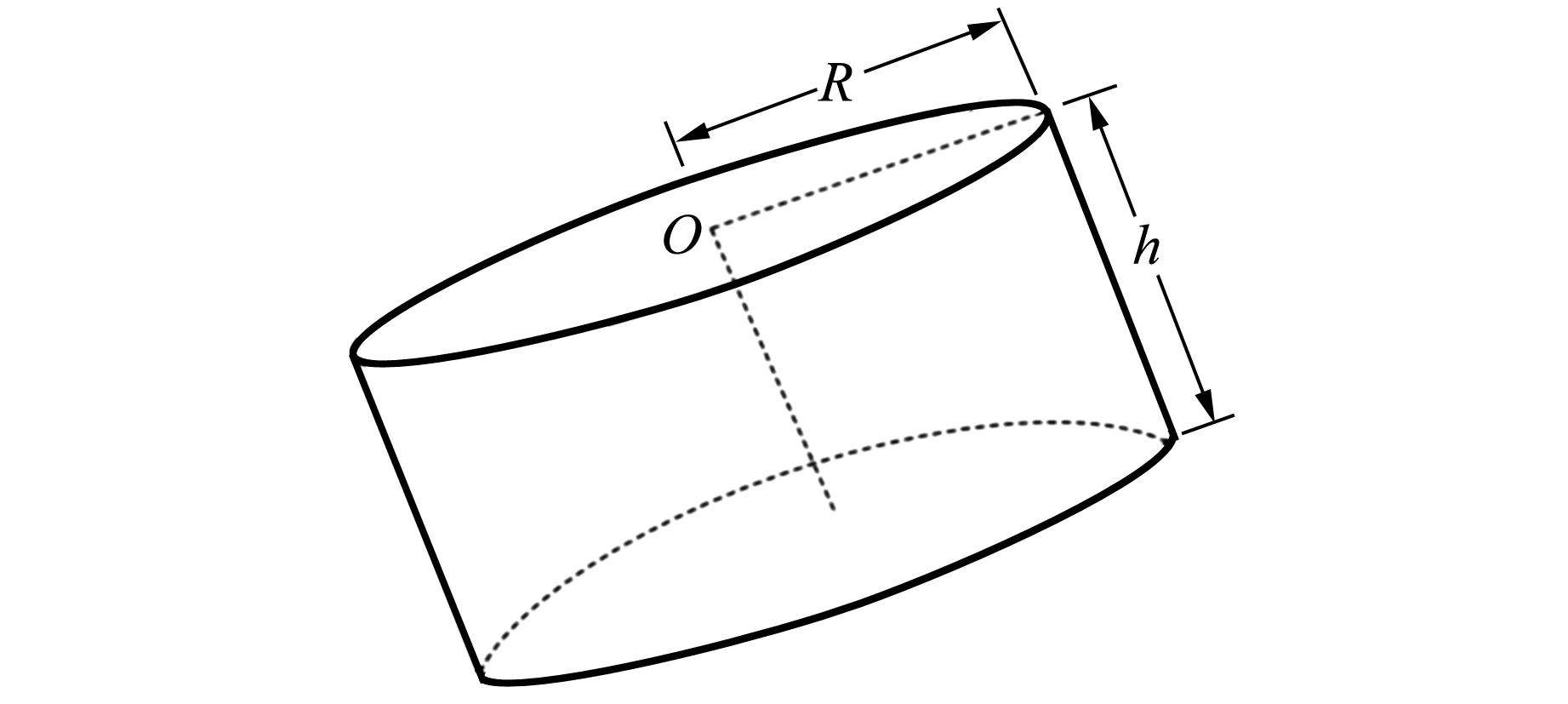
(a)立体图
(1)
则内角为
β=2arctan(2η),
(2)
(3)
2 骰子的投掷方式
研究者们大都假设三面骰子竖直下落,而不具有水平方向的速度,下面给出简单的理论解释.
假设在t=t1和t=t2时刻,系统的位置由2组坐标q(1)和q(2)确定,则系统在这2个位置之间的运动积分
(4)

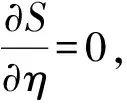
(5)
故
(6)
函数L为给定系统的拉格朗日函数或拉格朗日量,积分S为作用量.
当仅考虑三面骰子落地时的状态(落地前的运动行为不考虑),假设骰子在地面沿直线滚动.现以三面骰子向前滚动时的2种极端的运动方式为例,即侧面滚动和正反面轮流翻滚(图2).利用式(1)求出这2种运动方式的η值,其他运动方式的η值介于这两者之间.

(a)侧面滚动 (b)正反面轮流翻滚
2.1 侧面滚动

(7)
(8)
拉格朗日量
(9)
根据拉格朗日方程,则有
(10)
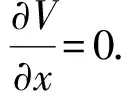
(11)
积分可得
x=C1t+C2.
(12)
2.2 正反面轮流翻滚
如图2(b)所示,骰子势能V不再是常量,并其转动惯量为
(13)
故动能可表示为
(14)
拉格朗日量为
(15)
根据拉格朗日方程可得:
(16)
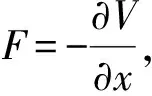
(17)

(18)
对比图2(a)和图2(b),可以看到在图2(b)情况下,骰子会受到额外的耗散力影响,因此图2(a)消耗能量较少,图2(b)消耗能量较多,其他运动状态则介于二者之间.由于圆形物体滚动时,其重心高度相对于地面接触点不变,滚动时不需要克服重力做功,处于能量最低态,是最稳定的运动方式.因此骰子总是趋向于侧面着地.
在现实情况中,首先骰子会受到地面的影响,使得骰子滚动时的轨迹为曲线,但曲线轨迹并不会影响结论;其次,滚动摩擦力比最大静摩擦力小得多,侧面滚动主要受到滚动摩擦,正反面翻滚主要受到最大静摩擦,即前者相比后者更能保证运动最大量,可以很大程度上减小克服摩擦力做功.因此,即使考虑摩擦影响,骰子也是趋向侧面滚动状态.所以可得出以下结论:三面骰子如果具有水平方向的初速度,骰子总是趋向于侧面着地向前滚动.性质会影响骰子立地概率的公平性,从而导致实验结果与实际情况不符.
那么,是否可以得出具有一定厚度的三面骰子都是趋向于侧面着地的结论呢?对此,对不同尺寸的三面骰子的着地情况进行统计,结果如表1所示.
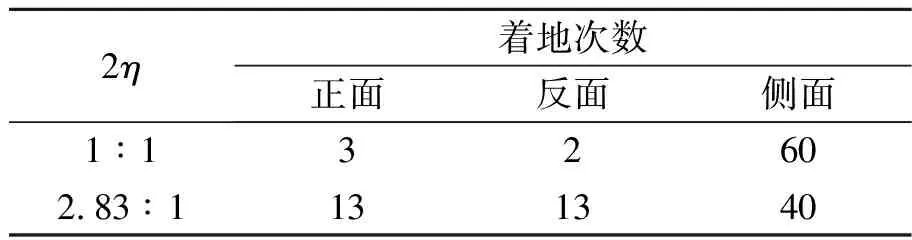
表1 不同尺寸的三面骰子着地的情况
实验采用的骰子直径2R=2.500 cm,h=0.833 cm,如若不给初速度,正常投掷,大都会认为骰子正反面着地的可能性大,然而表1却是侧面落地的次数多,表明骰子向前投掷会增加侧面着地的概率,与理论猜想相同.
同样利用硬币进行翻滚实验时,大多数情况下也都是侧面向前滚动的情况,但由于硬币的侧面尺度很小,立地条件不足,容易受到外界扰动的影响,所以不论怎么抛掷都不会影响公平性.
如果地面光滑,采用向前抛掷的方法,硬币便不会受到外界扰动,将保持自身的惯性,从而有可能出现侧面立地的情况.因此,在投掷圆柱形骰子时,尽量保持骰子在水平方向无初速度.
3 三面骰子实验设计
图3所示骰子是以ABS材质为原材料的实心圆棒,利用游标卡尺测量长度,通过手工锯和锉刀切割磨皮,虽以上制作方法存在较大误差(手工切割所带来的正反两面的不对称),但由于目前只是验证模型,即只需证明侧面出现的概率接近1/3,因此可以忽略误差带来的影响.骰子直径固定2.500 cm,制作不同高度的骰子,实验时1次性投掷5个相同高度的骰子,多个数据点可以避免单一骰子带来的固有偏差[3].

图3 手工骰子
第2章已证明三面骰子水平方向不应具有初速度,为了避免这种情况,设计了如图4所示的投掷装置.
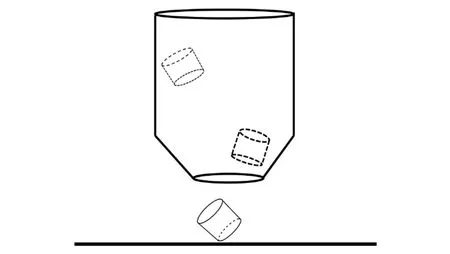
图4 投掷装置示意图
将骰子从宽口丢下,让骰子充分旋转,在骰子接近窄口时,由于路口变窄,骰子剧烈震荡,骰子的转动动能部分损失,并转化为竖直向下的动能,这样就满足了第2章中论述的限制条件.改变投掷装置的高度,可改变骰子的弹跳情况.投掷装置采用5 L矿泉水桶裁去桶底部分制作.
当三面骰子竖直落地时,由于边缘落地带来的反弹,能量在竖直方向可能无法抵消,从而让骰子具有水平方向的动能(在同一竖直线反复弹跳的结果不太可能出现),那么当出现该情况时,需要舍弃该结果并重新投掷.此外,设计骰子分别在水泥和PVC材质的接触面上着地.
4 三面骰子模型
在完全不考虑反弹的情况下提出了3种三面骰子的模型,出发角度各不相同,得出的结果也有差异.为了验证前文内容,设置了3种实验环境:在无初速度时水泥面和PVC面着地,以及有初速度时,骰子在水泥面着地的情况.
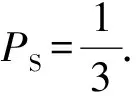
4.1 圆柱体表面积模型
通过借鉴标准正方体骰子出现等概率性的特性,猜想表面积可能是影响因素之一,于是得出:
(19)
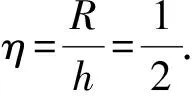

表2 圆柱体表面积模型骰子着地情况
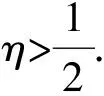
4.2 立体角模型

(a)立体图
设球冠的表面积为A,利用微元法求解.在球冠上取细小的圆环,半径为r,弧长为dl=Rdθ,于是面积为
dA=2πrdl=2πrRdθ,
(20)
(21)
因r=Rcosθ,则
(22)
(23)
由立体角公式,有
(24)
为使其平均,应该使得立体角为
(25)
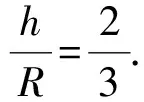
(26)
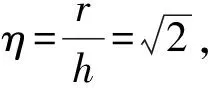

表3 立体角模型骰子下落情况
由表3中数据得:水泥接触面时骰子的正面概率PA=0.443,反面概率PB=0.383,侧面概率PS=0.174;PVC接触面时骰子的正面概率PA=0.427,反面概率PB=0.363,侧面概率PS=0.210.很明显,侧面概率与理想值0.333有较大偏差.故冯诺依曼假设仅在数学模型上合理,但与实验结果不符.
4.3 重心模型
图6为三面骰子落地时与接触面接触时的一种状态,重心线的偏向决定了三面骰子倒地的结果[5],θ为重心线与x轴的夹角,OH为重心线,决定骰子的偏向.
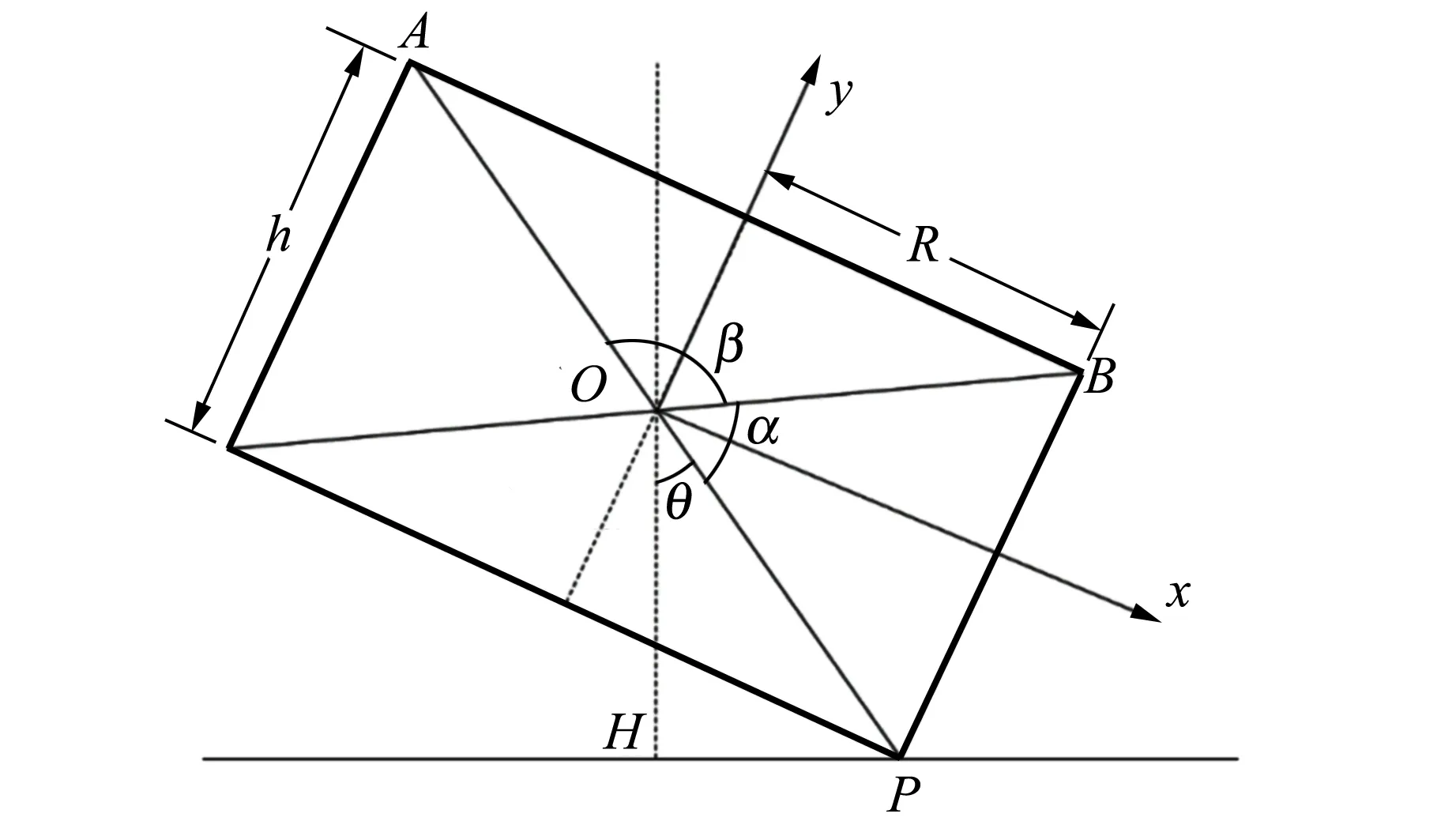
图6 圆柱骰子截面图
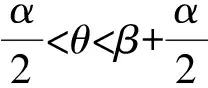

表4 重心模型下骰子下落情况
由表4中数据可得:接触面为水泥且无初速的条件下,骰子正面概率PA=0.335,反面概率PB=0.322,侧面概率PS=0.343,侧面相对偏差Er=3.0%;接触面为PVC且无初速的条件下骰子正面概率PA=0.320,反面概率PB=0.351,侧面概率PS=0.328,侧面相对偏差Er=1.5%.数据与理论吻合较好.
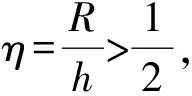
5 弹跳模型
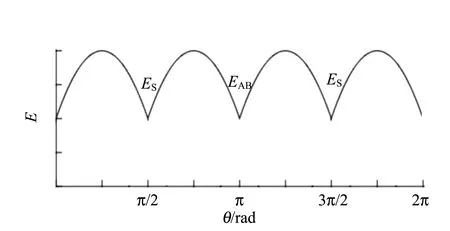
上文仅考虑了三面骰子落地瞬间便损失全部动能的情况,现以简单弹跳情况为例进行分析.假设每次落地损失一部分动能,即三面骰子经过多次反复弹跳才会停止,并且每次落地弹跳之后会经过充分旋转,再次落地时方向依旧随机.假设初始时,三面骰子具有能量E,第一次与地面碰撞后能量为γE,第n次碰撞后能量为γnE(n=1,2,3…),其中γ<1为衰减系数[6].
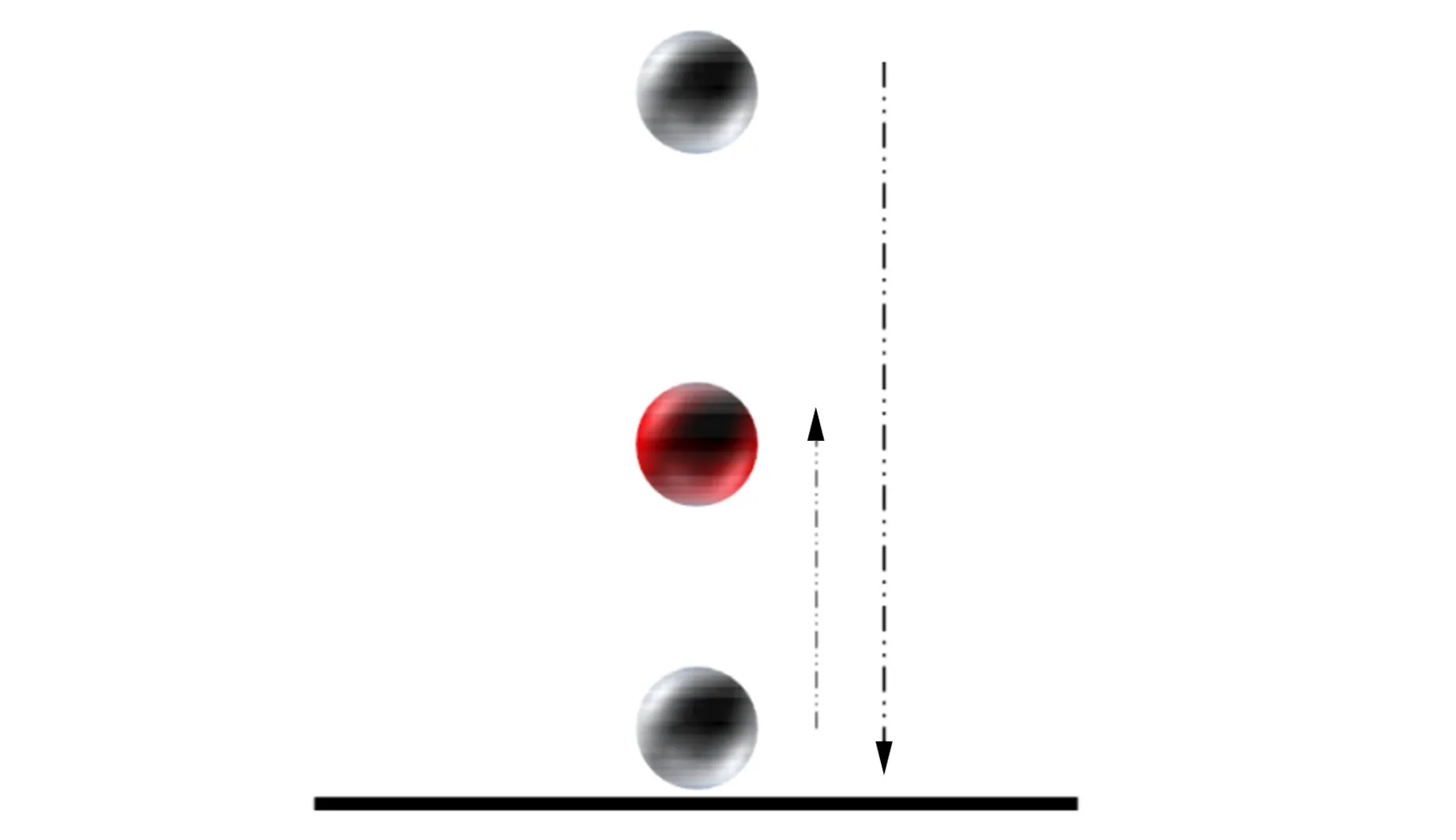
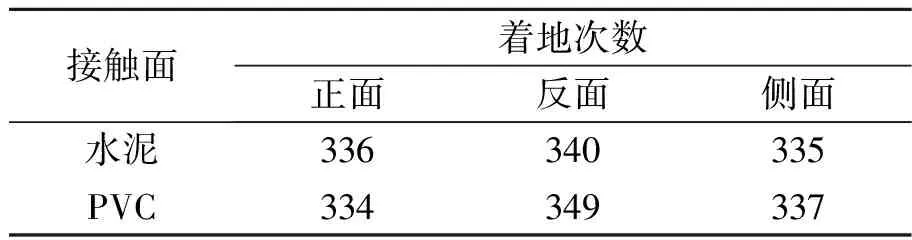
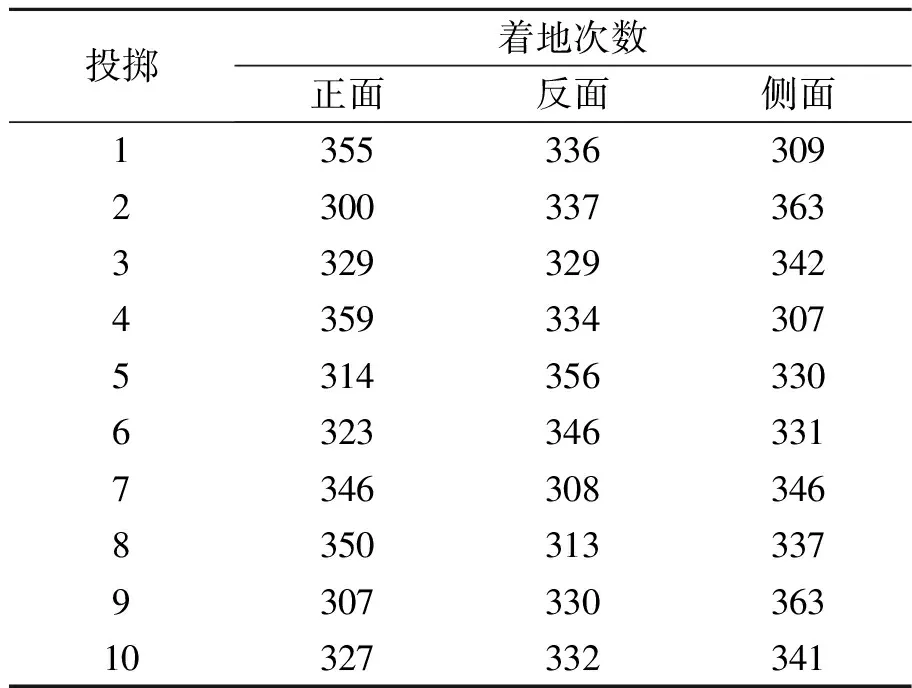
定义2个能量值EAB和ES,它们分别表示底面和侧面的能量势阱,如图7所示.假设底面的势阱高,即ES>EAB(若ES 图7 ES>EAB情况下对应的能量势阱图 此时落在2个山谷的概率正比于两侧山峰的间距,则会出现如下情况: 1)假设经过n次弹跳,能量为EAB<γnE,γn+1E (27) 该假设还可以表述为:假设前m次碰撞,其能量为γmE>ES,而EAB<γm+1E 2)假设经过n次碰撞后能量为γnE (28) (29) (30) (31) 现考虑式(28),则 (32) (33) 该结果与式(30)和式(31)相同. 当ES=EAB时,对应如图8所示的能量势阱.骰子经过n次弹跳后,能量为γnE 图8 ES=EAB情况下对应的能量势阱图 (34) 此条件下得到的结果,与前面结果相同,但此种情况很特殊,等式成立的条件比不等式成立更加苛刻,因此不易实现. 在本节中,得出结论有:三面骰子不允许多次弹跳,否则实验结果会出现很大偏差.所以实验过程中要求三面骰子落地后,动能必须立刻损失或弹跳1次后减为零,否则将不会出现等概率事件. 在构造弹跳模型时,没有给出E和r的数值,因此做了如下假设: a.每次碰撞后的能量衰减参量不变,并且各个接触点的衰减参量都相同; b.每次弹跳落地前都经过充分旋转,落地后再次随机; c.E和γ不同取值不会导致其他影响; d.从始至终只有骰子的竖直方向有动能,且反弹不会带来方向的偏移. 上面4个假设的约束性较强,使得弹跳模型局限性较大.根据热力学模型的建立过程可知,模型的限制越多,模型与实际情况就越可能畸变.三面骰子不像正方形骰子、异体形骰子,每个面都有精准的对称性,因此需做出一些条件假设求解三面骰子模型. 根据本节内容,n=0的情况与4.3节相同,现给出n=1,2时的实验数据,如表5~6所示. 表5 n=1,η=时骰子的下落情况 由表5可知:当n=1,接触面为水泥时,骰子的正面概率PA=0.330,反面概率PB=0.349,侧面概率PS=0.321,侧面相对偏差Er=3.6%. 猜想n=0,1情况下,实验结果相差不大的原因只是由于碰撞1次带来的效果不特别明显,为了满足骰子只碰撞1次,需要调节高度来实现,在实验中,这种高度不足以产生特别明显的误差.圆柱形骰子是不完美对称的,因此碰撞之后会使骰子的运动方向改变.因此骰子具有水平方向的初速度,也会导致侧面的概率发生变化. 由图9可以看出,不完美对称的物体反弹以后,会偏离原来的运动方向,由能量守恒可知,骰子具有了水平方向的速度,根据第2章内容,骰子侧面着地的概率将会增加. (a)高度对称球的反弹 通过简单的测试发现,骰子竖直落下,发生弹跳,侧面着地的次数会大大增加(表7),这样的结果与第2节的内容相符.所以给出的结论是:实验过程中,保持n=0才最为合理. 表7 发生弹跳后的骰子下落情况 表6 n=2,η=0.391 2时骰子下落情况 综上所述几何和反弹模型共同说明:圆柱形骰子须无反弹、无水平初速度的投掷才能保证其等概率着地. 图10 3D打印骰子 表8 标准骰子的下落情况 接触面为水泥面时,骰子正面概率PA=0.332,反面概率PB=0.336,侧面概率PS=0.331,侧面相对偏差Er=0.6%. 接触面为PVC面时,骰子正面概率PA=0.327,反面概率PB=0.342,侧面概率PS=0.330,侧面相对偏差Er=0.9%. 利用Pycharm软件进行模拟如图11所示,模拟投掷次数为1 000次,做了10次模拟的数据如表9所示. 表9 Pycharm软件模拟投掷情况 图11 Pycharm软件模拟 从实验数据上可以看出,实验结果与理论分析较吻合,如果需要更接近333的数据,可以通过调节滚动摩擦力来实现.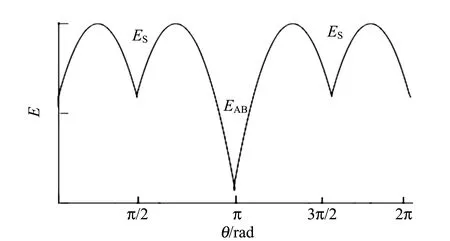

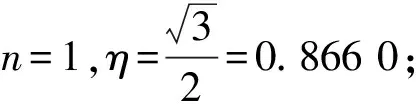

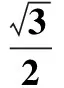
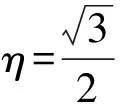

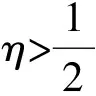

6 标准骰子实验


7 结 论


