基于“再创造”的数学史与数学课堂教学融合

刘嘉　王秀彩

编者按：为推进中学数学教育教学改革与发展，促进教育工作者理论素养和专业水平的提升，搭建优秀教学交流平台，在中国教育学会中学数学教学专业委员会的支持下，中国数学教育杂志社举办了“2022年度中国数学教育论文评选活动”. 在此次活动中，多篇选题新颖、内涵丰富的文章脱颖而出. 为进一步激发教育工作者的写作热情，并对此次活动中的获奖者表示祝贺，《中国数学教育》杂志将分批次择优刊登“2022年度中国数学教育论文评选活动”中的获奖文章. 同时，欢迎各位读者积极参与“2023年度中国数学教育论文评选活动”.

摘  要：以“椭圆及其标准方程”一课的教学为例，在弗赖登塔尔“再创造”理论的支持下，进行数学史和数学教学融合的尝试. 对椭圆概念和椭圆标准方程发生、发展的历史进程进行改造和重建，包括梳理椭圆概念历史发展过程中的关键环节，从一个环节发展到下一个环节的动因，以及数学家所面临的困难和障碍. 在此基础上，结合学情重构相关环节，并调整一些环节的历史顺序，使之适合课堂教学，设计出一系列由易至难的问题串，引导学生逐步完成对知识内容的再创造.

关键词：数学史；数学教学；再创造

《普通高中數学课程标准（2017年版2020年修订）》指出，通过数学概念和思想方法的历史发生、发展的过程，一方面，可以使学生感受丰富多彩的数学文化，激发学生数学学习的兴趣；另一方面，有助于学生对数学概念和思想方法的理解. 但是数学概念和思想方法的历史发生、发展过程和数学教材的呈现顺序往往存在较大的差异. 以椭圆概念的历史发展过程为例，从数学史上看，椭圆概念的形成大致可以分为三个时期：古希腊时期的截线定义；17世纪的动点轨迹定义；1822年比利时数学家旦德林将截线定义和动点轨迹定义统一. 椭圆概念的历史发展过程如图1所示.

在实际教学过程中，教师往往会从17世纪舒腾给出的三种作图法之一出发：在平面内固定两点，绷紧一根定长（大于两固定点之间的距离）的绳子绕两点旋转一圈得到椭圆，随后给出17世纪洛必达对椭圆的定义，利用定义推导椭圆的标准方程，进而引导学生对椭圆的性质展开研究. 但是这种在教学中通常使用的处理方法与椭圆概念发生、发展的历史并不是完全一致的.

数学教学中类似的例子比比皆是. 这说明：在数学教学中，不应该只是简单地重现真实的历史，而应该是对历史的适当重建，即对数学史素材进行适当“改造”，使之能够更好地服务于课堂教学目标. 这与数学教育学家弗赖登塔尔提出的“再创造”理论基本吻合.

一、“再创造”理论指导下的数学史和数学教学融合

弗赖登塔尔认为，数学教育必须面向社会现实，必须联系日常生活实际，注重培养和发展学生从客观现象中找出数学问题的能力，用“再创造”的方法进行教学. 他还认为，“再创造”应该贯穿数学教育的全过程，教师的任务就是引导学生参与概念、法则、定律等形成的全过程，为学生提供广阔的天地，听任不同的思维和方法自由发展，不要对学生的发现设置任何圈套.

由于学生个体学习数学的进程和数学发展的历史之间存在一些相似之处，所以教师可以创设与相关数学概念、法则、定律等发生、发展过程相似的情境，引导学生经历这些概念、法则、定律等产生的过程，并引导学生结合自己独立的学习体验，完成对概念、法则、定律等的再创造.

正如数学教育学家波利亚所说：我们应该让儿童重演人类心理演进的重大步骤. 当然，我们不用让他重复过去一千零一个错误，而只是重复“重大步骤”. 由于相关概念、法则和定律发生、发展的历史并不一定符合学生的思维习惯，因此教师在创设数学史情境引导学生完成对数学教学内容的再创造时，往往需要对历史素材进行改造和重建. 下面以椭圆概念的再创造为例进行说明.

如前所述，椭圆概念的发生、发展历史和目前大多数教师常用的教学设计并不太一致. 之所以这样，是因为尽管从平面截圆锥引入椭圆非常自然，且符合学生的已有认知基础，但是要从椭圆的截线定义过渡到椭圆的轨迹定义是非常艰难的. 因此，教师放弃了平面截圆锥的引入方式.

但是近年来由于信息技术在教育领域的广泛使用，使得我们可以借助信息技术突破从椭圆的截线定义过渡到椭圆的轨迹定义的难点，因此教学中也可以考虑基于数学史素材创设情境，引导学生经历椭圆概念的演变过程，并重复其中的“重大步骤”，完成对椭圆概念的再创造.

1. 创设情境，引入椭圆的截线定义

如图2，使用学生生活中常见的椭圆形的建筑、倾斜烧杯中的水面椭圆等引入椭圆，这样符合学生的认知规律. 学生很容易指出这些图形叫椭圆.

紧接着，教师便可以抛出历史素材：古希腊数学家阿波罗尼奥斯发现用平面截圆锥可以得到不同的曲线，今天我们将这些曲线统称为圆锥曲线. 其中，当截面和底面夹角小于母线和底面夹角时，所截得的曲线称为椭圆（如图3）.

我们在这里对历史素材进行了改造. 实际上，在阿波罗尼奥斯之前，古希腊的学者们在研究倍立方问题时被引到了对圆锥曲线的研究上. 例如，欧几里得在《几何原本》第6卷中谈到了用垂直于母线的平面截锐角圆锥、直角圆锥、钝角圆锥所得的曲线. 这里我们忽略了这部分历史，正如波利亚所说，我们只需引导儿童经历其“重大步骤”.

2. 探究新知，发现椭圆的轨迹定义

由截线定义所得的椭圆和学生已有认知中的椭圆完全相符. 因此，学生接受起来十分自然. 接下来，我们可以借助信息技术引导学生完成从椭圆的截线定义到椭圆的轨迹定义的过渡.

这里，我们需要再次对历史进行改造和重建. 我们可以将1822年旦德林的工作放到17世纪洛必达的轨迹定义之前，之后再进行作图验证，最后得到椭圆的标准方程，如图4所示.

在数学教学中，像这种对数学概念、法则、定律等发生、发展的历史顺序进行改造重建的例子非常多. 例如，从指数的逆运算引入对数更简洁，但是历史上却是在对数诞生数百年后，才由数学家欧拉指出了指数和对数的关系. 有时候，数学的发展史并不一定符合学生的认知习惯，因此对数学发展的历史顺序进行改造和重建非常必要.

如图5，大球和小球都和圆锥面相切，平面和大球相切于点[F1，] 与小球相切于点[F2.] 通过度量，学生发现当点[P]在椭圆上运动时，[PF1+PF2]为定值. 之后可以设计探究活动，引导学生思考、论证为何[PF1+][PF2]的值为定值. 事实上，由于[PF1，PN]均为大球的切线，所以[PF1=PN.] 同理，[PF2=PM.] 所以[PF1+][PF2=MN，] 为定值.

通过此探究活动，学生借助信息技术带来的直观体验，实现了对椭圆概念的再创造：椭圆是平面内到两定点距离之和为定值（大于两定点间的距离）的点的轨迹.

3. 应用新知，设计椭圆绘图工具

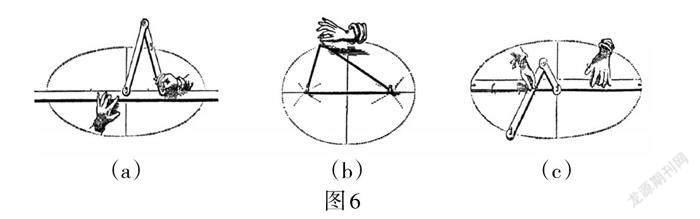
从历史上看，17世纪笛卡儿在《几何学》中对圆锥曲线方程的研究引起了数学家对圆锥曲线作图方法的探究. 法国数学家舒腾给出了椭圆的三种作图工具（如图6），其中图6（b）就是利用了椭圆上的点到椭圆两焦点距离之和为常数.

课堂上，教师也可以设计活动，让学生经历这个历史过程，既有助于学生对椭圆概念的理解，又能够培养学生将数学知识运用到处理实际问题中的能力. 因此，在得到椭圆的定义后，教师可以进一步让学生设计一种能够绘制椭圆的工具. 根据探究所得，学生能够想到在平面内固定两点，绷紧一根定长的绳子（大于两定点间的距离）绕两点旋转一圈绘制的图形便是椭圆.

如果学情允许，教师可以进一步提供舒腾的另外两种绘制椭圆的工具，让学生运用所学知识得到椭圆的概念，并论述使用这些工具绘制的曲线的确为椭圆.

4. 巩固新知，推导椭圆标准方程

在学生完成椭圆绘制工具的設计后，教师引导学生经历椭圆概念发展历史中的又一“重大步骤”，即椭圆标准方程的建立. 这始于17世纪笛卡儿在其著作《几何学》中的工作. 同时，对椭圆标准方程的推导往往也是椭圆起始课的一个重要教学目标. 数学史素材的使用，始终是为达成教学目标而服务的.

可以发现，洛必达的方法能避免二次平方带来的烦琐运算，使学生体会到对称的思想，提升他们的数学运算素养.

至此，教师通过对椭圆概念发生、发展的历史进行改造和重建，使其变成了适合学生课堂探究的素材，并引导学生完成了对椭圆的概念和标准方程的再创造.

二、结论

教师通过对数学史素材进行筛选、改造和重建，利用历史素材创设适合学生“再创造”的情境，引导学生经历数学内容发生、发展的历史过程，有助于增强学生的学习动机，促使学生保持对数学的兴趣，解释数学在社会中的作用及数学与其他学科的关联. 同时，历史上数学概念、法则、定律等发展的障碍，有助于学生认识到学习中的困难. 数学家突破这些障碍的事迹，以及在突破障碍过程中运用的思想方法等，有助于学生增强克服困难的勇气和决心. 通过近距离感受数学大师的风采，使学生更深刻地理解学习的内容.

教师在“再创造”理论指导下进行数学史和数学教学融合的设计，对教师也提出了更高的要求. 教师要了解所讲授知识内容的历史发展过程，能确定历史发展过程中的关键环节，从一个环节发展到下一个环节的动因，以及数学家所面临的困难和障碍，并在此基础上，重构这些环节，使之适合课堂教学. 同时，要在此基础上设计一系列由易至难的问题串，引导学生逐步完成对知识内容的再创造.

参考文献：

［1］中华人民共和国教育部. 普通高中数学课程标准（2017年版2020年修订）［M］. 北京：人民教育出版社，2020.

［2］汪晓勤，王苗，邹佳晨. HPM视角下的数学教学设计：以椭圆为例［J］. 数学教育学报，2011，20（5）：20-23.

［3］邹佳晨. 椭圆的历史与教学［D］. 上海：华东师范大学，2010.

基金项目：北京市教育学会“十四五”规划立项课题——基于核心素养培养的数学史与高中数学课堂教学深度融合研究（CYYB2021-346）.

作者简介：刘嘉（1983— ），男，中学高级教师，主要从事数学史与数学教学融合研究；

王秀彩（1971— ），男，正高级教师，北京市特级教师，主要从事高中数学大单元主题教学结构化研究.