统领设计,适时渗透,凸显核心
陈棉驹
笔者所在地区推进初中数学渗透数学思想方法的教学实践,经过多年推广取得了一定的成效,相当部分教师已能自觉运用数学思想方法开展教学。2022年6月,笔者参加区里一所初中的高效课堂评估活动,其中一位青年教师执教的课“多边形内角和与外角和(第1课时)”(北师大版数学教材八年级下册)备受好评。这节课教学设计巧妙,教学中自然而又适当地渗透和呈现了转换与化归、分类讨论、数形结合等数学思想方法,培养了学生抽象能力、几何直观、推理能力等数学核心素养,达成了较好的教学效果。
然而由于教师对于数学思想方法的核心理解不够到位,对其关键要素把握不够准确,导致数学思想方法的教学未能深入开展。为推进渗透数学思想方法教学的进一步深化,本文将对该节凸显数学思想方法的优质课作简要叙述和点评,对部分教学的处理提出改进建议,并对数学思想方法教学如何走向深入提出思考。
一、凸显数学思想方法教学的课例切片分析
环节1:课前回顾
教师引导回顾四边形内角和的探究方法,通过连接对角线将四边形分割为两个三角形,为后续多边形分割为三角形提供了思路和方法的类比对象。
环节2:课堂探究
活动1:探究多边形内角和。教师让学生自主探究五边形的内角和,学生自然地从一个顶点出发连接两条对角线,将五边形分割为三个三角形,从而得出五边形内角和为3×180°=540°。
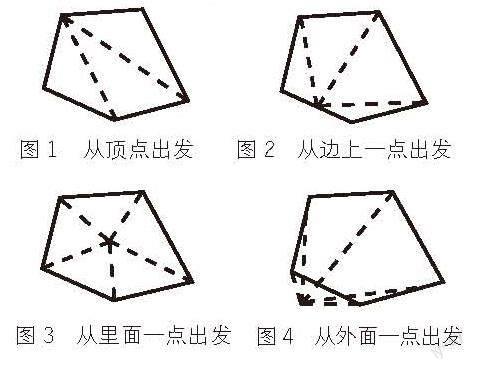
活动2:探究其他的分割方法。学生经过独立思考和小组讨论,给出了将五边形分割为三角形的其他方法,教师结合图形归纳分割方法为从顶点出发、从边上一点出发、从里面一点出发、从外面一点出发(如图1至图4)。学生展示分割的图形后,教师用几何画板演示,并提问是否还有其他分割方法,学生回答应该还有其他的方法。
活动3:探究n边形的内角和。从五边形推广至六边形、七边形,直至n边形,通过表格呈现计算内角和的式子,学生分析内角和与边数关系的规律,得出多边形内角和公式。
活动4:对应练习。①九边形内角和是?②一个多边形内角和是900°,它是边形?
教学改进建议一
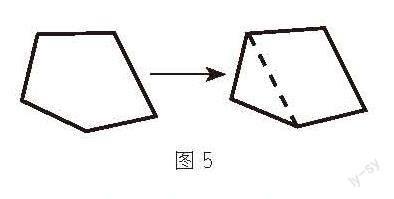
此环节教师运用转化思想指引学生探究多边形内角和,将未知的、复杂的多边形问题转化为已知的、简单的三角形问题,通过不同的分割方法(分割是转化思想指导下的具体操作),让学生明确问题解决的关键——将多边形问题转化为三角形问题,为之后特殊平行四边形的学习、几何问题的解决提供了有益的经验。然而,将多边形分割为三角形虽然是问题解决的关键,却不是转化思想的核心,转化思想的核心是将新知转化为已知,将复杂转化为简单,将高维转化为低维。对本问题而言,三角形的内角和为180°是已知的,四边形的内角和为360°同样是已知的,探究多边形(边数大于4)内角和时,将多边形转化为三角形和四边形的组合(如图5),这种分割方法不仅是可行的,更有助于提醒学生关注转化的核心,是有价值的。目前分割方法只关注了转化的形式,却忽略了转化的本质。
活动2中,学生经历独立思考、小组讨论,教师归纳总结,得到将五边形分割为三角形的四种方法,培养了学生分类讨论的意识。然而,教师教学时忽略了对于分类标准的讨论,也没有分析四种分割方法(即分类的四种结果)在逻辑上是否不重不漏。分类是在分类标准指导下进行的,只呈现分类结果而缺乏对分类标准的讨论,是目前不少课堂在渗透数学思想教学时的常见问题。对本问题而言,分类标准可以是点与多边形的位置关系,平面内的点只有在多边形的顶点、边上、内部以及外部四种情况,所以分割方法就只有四种,其他分割只是图形的变化,并没有本质的区别。建立符合逻辑的分类标准以指导分类,这样分类才能不重不漏。
经历图形分割后,活动3将几个特殊多边形的内角和计算式子以表格形式呈现,行列的对比分析有助于找到内角和与边数之间的规律,再推广拓展至n边形,通过图形分割寻找数量关系,体现以形助数的思想方法。然而,数形结合的本质应该是,对同一问题可以从数和形两个维度认识和理解,通过数形的转换和结合,使得对该问题的认识更加深刻。在本问题中,通过连线将多边形分割为三角形,如果从一个顶点出发(如图1),由于相邻两个顶点的连线是边,而非对角线,因此连接的对角线数量是n-2,从而分割成的三角形个数是n-2,因此n边形的内角和即为
(n-2)×180°。如果从多边形内一个点出发(如图3),n边形可以分割为n个三角形,内角和为n×180°,再减去中间的周角360°,则n边形的内角和为(n-2)×180°。结合图形分析或推导出边数n和公式中n-2的逻辑联系,从形和数两个维度,对多边形内角和形成更全面、更深刻的理解。
环节3:典型例题
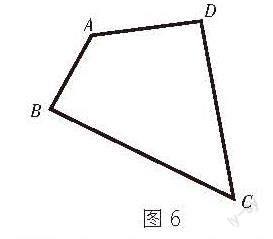
如图6,在四边形ABCD中,已知∠A+∠C=180°,猜想∠B和∠D的关系。
利用多边形内角和公式求出四边形内角和是360°,再减去已知的∠A与∠C之和,即可得结果∠B+∠D=180°。
例题来源于教材,是对多边形内角和公式的简单运用,进而得出一个结论:如果四边形有一组对角互补,那么另一组对角也互补。
环节4:议一议
剪掉一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?学生通过思考、画图(如图7)等具体操作后,利用多边形内角和公式解决。
教学改进建议二
议一议的问题来源于教材,原来编排在探究正多边形内角之后,教学中将其提前,作为典型例题之后的一个探究性问題,这样的安排使内容衔接更为连贯。学生自主解决或与同伴交流,对问题进行分类讨论,得到了三种剪切的结果,培养了思维的发散性。然而,对于思维严谨性和全面性的培养,还是略有欠缺。问题的关键如同前文提到的分割多边形,只讨论了分类的结果,却没有提出符合逻辑的分类标准。在本环节中,教师可以在学生得出分类结果后提出问题:还有其他的剪角方式吗?如果有请画出来,如果没有请说明理由。通过问题迫使学生进一步思考,反思其中的分类标准。教材将问题设置为议一议,不只讨论如何解决,更要讨论为什么这样解决,在表达、倾听、质疑、答疑中,提升学生的数学表达素养。
本问题分类的标准可以是剪切线与长方形交点的位置,即剪切线过两条边、剪切线过一条边一个顶点、剪切线过两个顶点,因此只有三种情况,分类不重不漏。
环节5:探究正多边形的内角
教师提问:能不能求得正五边形的每个内角?
学生回答可以先求出五边形内角和,再根据正多边形内角相等的性质,将内角和除以5,从而求得每个内角的度数。
最后推广出正n边形的每一个内角为。
教学改进建议三
问题源于教材,直接提问有利于集中学生的注意力,调动思维,解决问题。然而,由于问题在逻辑上存在跳跃,学生只能被动地解决问题,而无暇思考问题从何而来。在本问题中,教师可以利用问题串引导学生进一步深入思考。
教师:已知如何求多边形内角和,那么如何求每一个内角?(不要求学生回答,只是引起学生思考,同时体现思考问题的顺序,从整体到部分)例如任意五边形的内角能求出吗?
学生:不能。
教师:为什么?
学生:任意五边形每个内角不一样。
教师:怎样的五边形才能求出内角?
學生:正五边形。
教师:为什么?怎么求?
本课的两个探究蕴含着特殊与一般的数学思想,探究多边形的内角和体现了从特殊到一般的问题探究策略,探究正五边形的内角体现了特殊化的思想。多边形是抽象的、一般化的,难以直接进行研究,因此从具体的、特殊的五边形开始,探究如何将五边形问题转化为三角形问题,探究多边形内角和的度数与边数的关系,并逐渐拓展到六边形、七边形,最后推广一般化为n边形。对特殊情况的分析越透彻,一般化的推广就越顺利。而关于任意五边形和正五边形性质的思考,是让学生感受特殊化思想的一个很好切入点。任意多边形不具备的性质,通过边的特殊化,会得到内角相等的性质,即条件的特殊化会导致性质的特殊化,这个经验对于之后特殊平行四边形等的学习将有所帮助。
教学环节中还有对应练习、知识归纳、知识巩固、达标检测等环节,本文从略。
二、关于进一步深化数学思想方法教学的思考
1.提炼主要数学思想方法,统领教学设计
教材呈现的主要是问题和知识,教师一般也是围绕两者来进行教学设计,通过问题探究提炼知识,通过问题解决运用知识。而从知识到能力,从能力到学科素养,需要数学思想方法作为桥梁。为进一步深化数学思想方法教学,可以提炼该节课中蕴含的对问题探究、解决具有策略引领作用的数学思想方法,并从数学思想方法的视角,进行课堂教学设计。探究多边形的内角和,运用从特殊到一般的思想方法,从特殊的、具体的五边形开始,明确研究对象后,进一步思考研究的思路和方法。未知的是五边形内角和,已知的是三角形和四边形内角和,考虑运用转换与化归思想将五边形问题转化为三角形问题,具体的操作方法是分割(数学抽象为画线)。为了探究多边形内角和这个数量规律,借助图形分割的方法,其中蕴含着“以形助数”的数学思想。因此,本课的设计应以特殊与一般思想为主线,以转化和数形结合思想为重要辅助来进行教学设计。
2.适时渗透数学思想方法,贯穿教学过程
教学过程中应适时凸显相应的数学思想,一般而言,在新知探究中渗透数学思想,在解题应用中运用数学思想,在归纳提炼中显化数学思想。在探究多边形内角和时,渗透了转化、分类讨论、数形结合等思想方法。在例题和练习中主要渗透了分类讨论思想,在归纳时显化了问题解决关键的数学思想——转化。教师可将多边形内角和问题(未知),转化三角形内角和问题(已知),转化是数学思想(写在线下),具体方法是分割(写在线上),本节课要解决的问题、解决的思想、解决的方法就清晰地呈现出来。
3.凸显数学思想方法核心,促进教学深化
教师对数学思想方法的各要素应认识到位,教学时要凸显其核心,才能让学生理解数学思想方法的本质。转化思想的核心是将新知转化为已知,将复杂转化为简单,将高维转化为低维。转化为三角形只是一个方向,转化为四边形也未尝不可,当然,从向最简单转化、向更具有普遍适用性转化而言,转化为三角形是更合适的选择。分类讨论思想的渗透应该包括分类讨论的必要性、分类的标准、分类的结果、结果的讨论等,教学时不能只限于呈现分类的结果。数形结合不仅是以形助数或以数辅形,而是对同一个问题从形和数两个维度进行分析理解,寻求其中数与形的联系。对于多边形内角和问题的探究,既有图形分割,又有数式规律的探索,正是利用数形结合进行数学思想方法渗透的良好契机。
责任编辑 罗 峰

