基于降阶模型的中子扩散特征值问题的不确定性分析研究

梁鑫源,王毅箴,郝 琛,*

(1.哈尔滨工程大学 核安全与仿真技术国防重点学科实验室,黑龙江 哈尔滨 150001;2.清华大学 核能与新能源技术研究院,先进反应堆工程与安全教育部重点实验室,北京 100084)

堆芯物理计算是反应堆设计与分析的基础,随着堆芯建模和仿真精度提升,其计算代价和复杂度亦随之提升[1]。此外,核数据作为堆芯物理计算的重要输入参数,其不确定性会影响堆芯物理计算结果的精度。基于抽样统计不确定性分析方法[2],开展精细化堆芯物理计算的不确定性量化研究,其将面临高昂计算代价。因此有必要开展堆芯物理降阶模型(ROM)在不确定性分析中的应用研究。

降阶模型根据构建方法可以分为物理驱动和数据驱动两大类。物理驱动方法包括各种投影技术,如伽辽金(Galerkin)投影法,该方法需要修改控制方程,因此需要直接访问全阶模型(FOM)源代码。某些情况下,直接剖析和修改全阶模型是具有挑战性的,但其优点是机理清晰、可解释性强。数据驱动方法包括克里金法[3-4]和动态模式分解法[5]等,仅需在“黑箱”模式下运行模拟,以生成与某些定义输入相对应的输出,把这些输入和输出数据用作训练数据,通过机器学习等方法构建输入参数与降阶模型的函数关系即可,虽操作简单,但不如物理驱动方法机理清晰。龚禾林等[1]基于本征正交分解(POD)技术和机器学习构建了数据驱动式中子物理快速计算模型。Elzohery等[5]用一维两群瞬态中子扩散问题对比物理驱动和数据驱动降阶模型的效果,其中基于物理驱动的POD-Galerkin降阶方法表现出最佳计算精度。

对于降阶模型应用于不确定性分析的研究,Elzohery等[6]对二维两群瞬态中子扩散问题利用贪婪采样得到的降阶模型进行不确定性分析,对比全阶与降阶计算的样本均值和标准差的相对误差,验证了降阶模型应用于不确定性分析的可行性。

本文将POD方法与经典的求解偏微分方程的Galerkin投影法结合,针对二维两群中子扩散问题构建物理驱动的降阶模型,探析POD基函数的物理含义,并对POD-Galerkin降阶模型用于抽样统计不确定性分析的可行性进行研究。

1 POD-Galerkin理论方法

1.1 本征正交分解

POD方法的核心是在核反应截面数据扰动下,从已有的中子通量场变化数据中找到1组最优的正交基来代表其数据变化特征[7]。最常用的方法是快照法,最早由Sirovich等[8]提出。快照是指不同核反应截面输入下,堆芯中子通量场数值解的空间分布。设Y={y1(x),y2(x),…,ym(x)}是1个由足够多快照组成的快照矩阵,也称样本空间。其中:m为快照数;x为空间位置向量;yi(x)为第i个核反应截面样本输入下堆芯中子通量场数值解的空间分布。假设核反应截面扰动下,中子通量分布样本空间中的样本点yj(x)函数展开如式(1)所示:

(1)

式中:φi(x)为基函数或基向量;ci为基函数对应的系数。

本征正交分解的基本步骤为:1) 对快照矩阵进行奇异值分解(SVD)[1,6,9],奇异值的平方即特征值λ,左奇异矩阵即基函数矩阵;2) 将得到的基函数按照特征值的大小降序排列,按照所需精度截取前r阶基函数即POD基,用POD基对yj(x)进行低维近似,则yj(x)可表示为:

(2)

其中,r的选取规则为:

(3)

式中,ε为根据所需精度设定的值,一般情况下取99.99%即可。

1.2 POD-Galerkin方法

Galerkin投影法[10-11]的实现是通过将试函数本身当作权函数来构造微分方程的积分形式,从而求得微分方程的近似解。在与POD方法结合构建低阶模型时,其试函数即POD基,即将POD基作为权函数来构建低阶模型。本文对稳态二维两群中子扩散问题构建降阶模型:

(4)

(5)

(6)

(7)

式中:g为群数;Dg、Φg、Σa,g、νΣf,g、χg分别为g群的扩散系数、中子标通量、吸收截面、中子产出截面和裂变能谱;Σs,g→g′为从g群到g′群的散射截面。

将式(4)转化为矩阵形式:

(8)

(9)

(10)

(11)

根据POD方法,可设:

(12)

(13)

(14)

根据Galerkin投影法,将式(8)投影到POD基上:

(15)

(16)

(17)

式中,c1和c2分别为1群和2群的系数向量。

将式(15)简化为如下形式:

(18)

Ar=Ur,TAUr

(19)

Br=Ur,TBUr

(20)

式中,Ar、Br均为r×r阶矩阵。

本文所研究的扩散问题为两群,考虑分群构建降阶模型:

(21)

(22)

较多结果表明,对于大多数工程问题,r≈10～100时即能构造出满足精度要求的降阶模型[12-15],降阶模型正是因此得以提高计算速度。

1.3 降阶模型构建流程

降阶模型的构建计算流程如图1所示。具体步骤如下:1) 对扩散系数及各种截面等不确定参数充分扰动,通过大量重复全阶计算,得到不同状态下的中子通量数据,构成足够充分的样本空间;2) 对样本空间进行奇异值分解,根据式(3)进行截断,确定基函数的阶数r,从而选取最优的r阶POD基;3) 构建全阶系数矩阵A、B。再用Galerkin投影法计算出降阶系数矩阵Ar、Br,完成降阶模型的构建。

2 数值结果

2.1 TWIGL基准题

该基准题包含3种不同介质区域,其1/4堆芯几何布置如图2所示[16],无外中子源,左边界与下边界为对称边界,右边界与上边界为零通量边界,各区域截面参数列于表1[16],其中χ1=1、χ2=0。

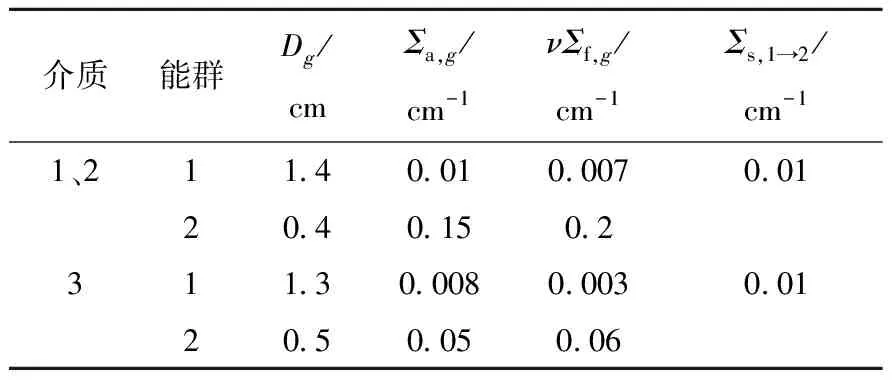
表1 TWIGL截面参数[16]

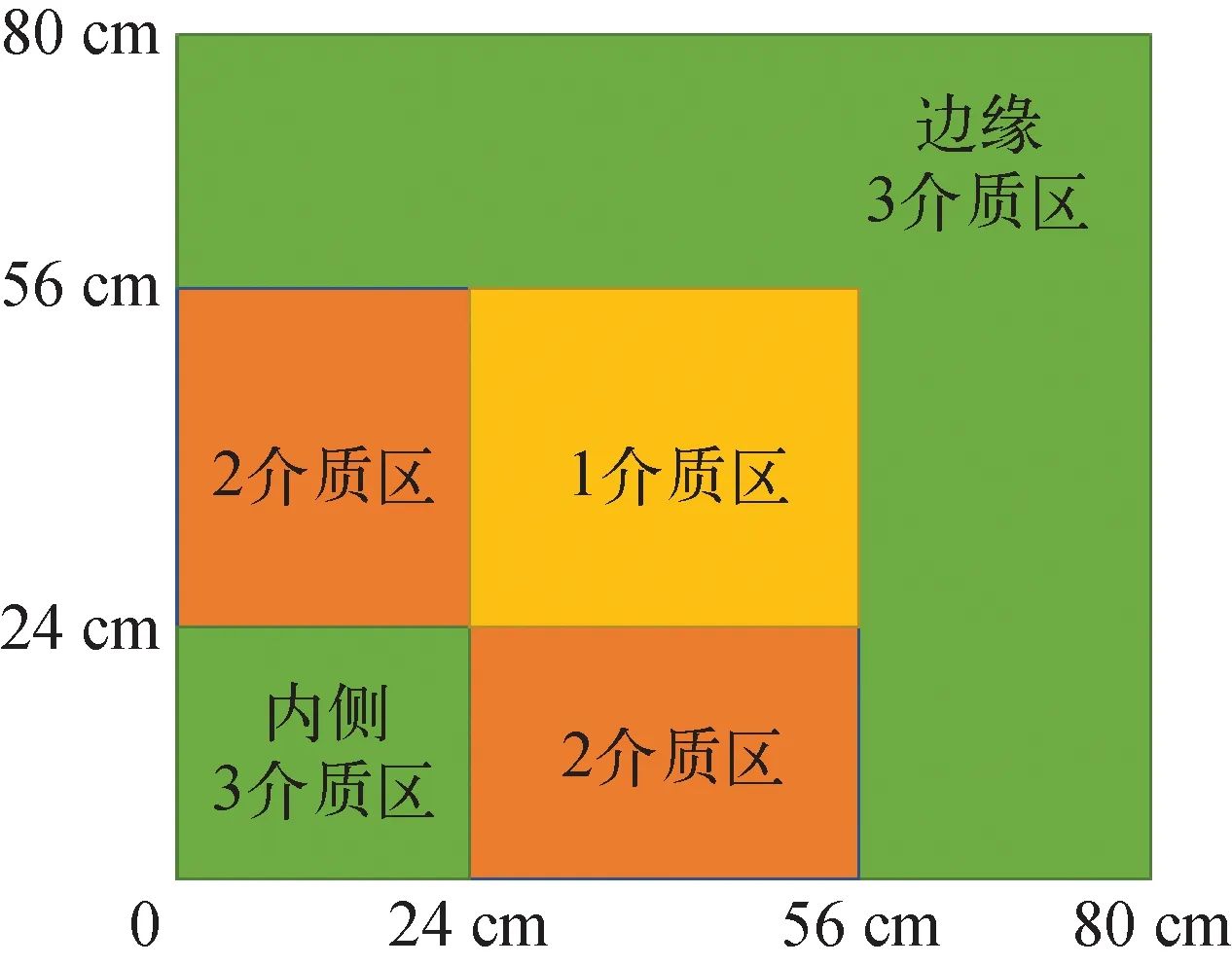
图2 TWIGL基准题几何模型[16]

2.2 计算结果与分析

根据1.3节计算流程,自主编写稳态二维双群扩散问题的全阶、降阶计算模型。

Elzohery等[6]在研究中发现,不同的网格尺寸对降阶模型计算精度的影响较弱,几乎可以忽略。网格划分越密,所需计算时间越长,本文采取120×120的网格尺寸。据文献调研[17],核截面扰动范围一般不超过40%,因此本文将扰动范围定为基准题给定值的20%。扰动基准题中的14个不确定参数,在扰动范围内随机采样100个点,进行全阶计算生成样本空间,对样本空间进行POD分解,将分解所得特征值进行降序排列,计算每阶特征值占比,前10阶的特征值占比曲线(对数坐标)如图3所示,可以看出,随着阶数增加,各阶特征值占比迅速下降,由式(3)得精度条件ε=99.99%时,快中子群和热中子群所需POD基的阶数分别为r1=2、r2=2。

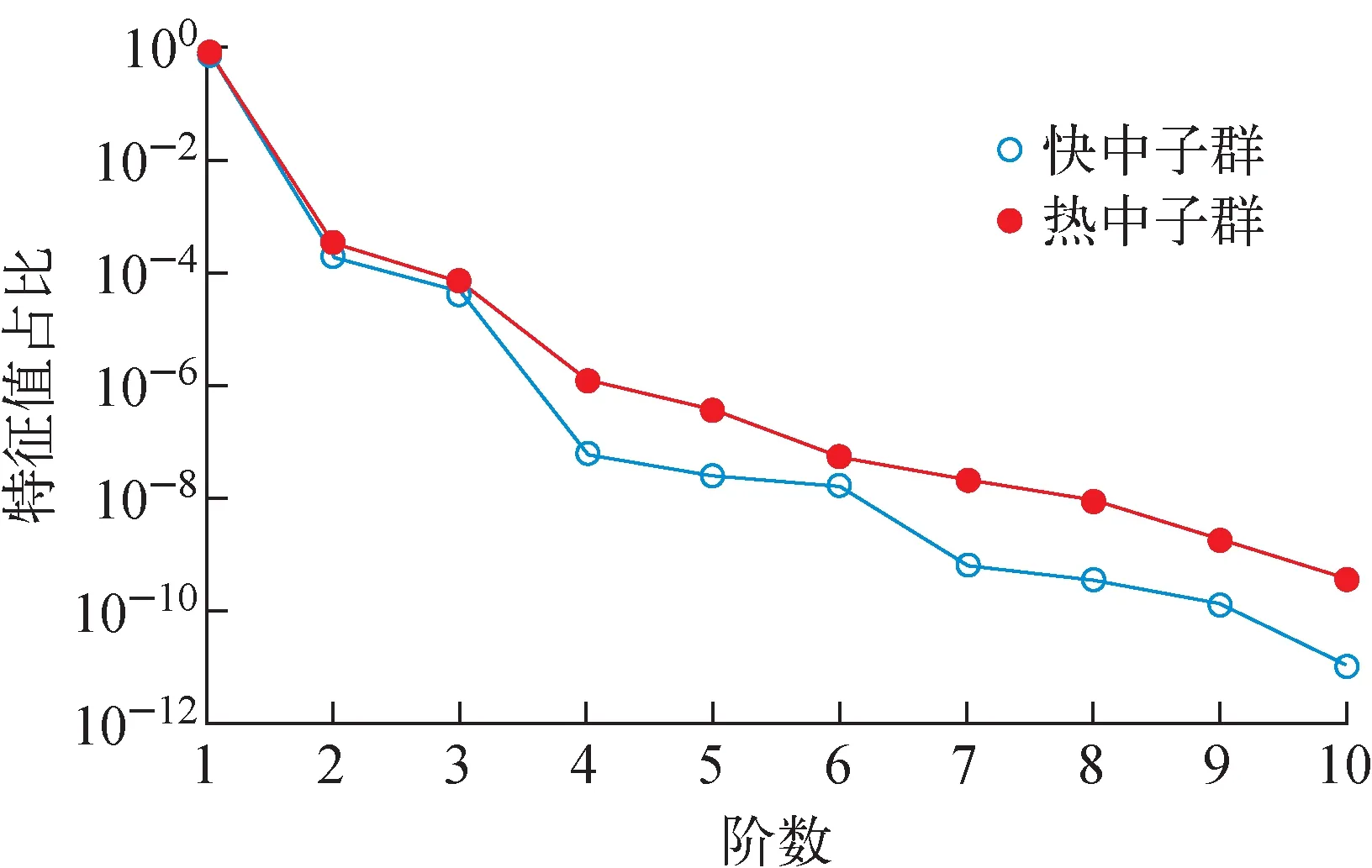
图3 前10阶特征值占比

在原基准题条件下,构建出降阶模型,全阶模型本征值计算结果为0.913 23,基准解[18]为0.913 21,两者偏差为2 pcm。降阶模型本征值计算结果为0.913 22,与基准解偏差为1 pcm。通过全阶模型与降阶模型计算的中子通量分布分别如图4、5所示。降阶与全阶的中子通量最大相对误差为:1群0.28%,2群0.28%。单次运算全阶模型的计算时间为54.50 s,降阶模型的计算时间为0.56 s,仅占全阶的1.02%。

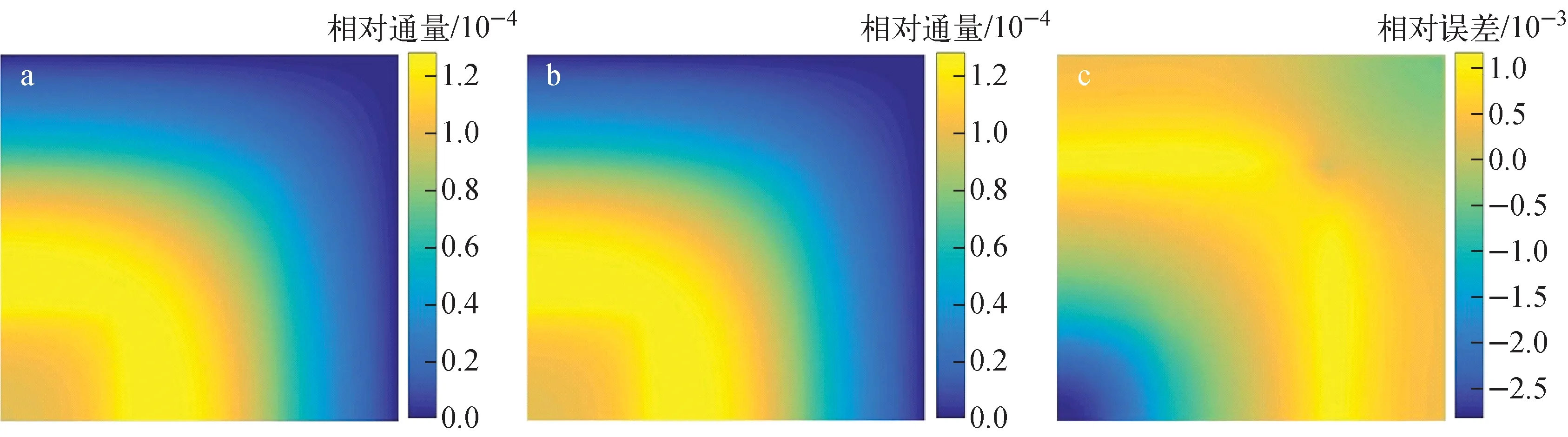
a——全阶模型;b——降阶模型;c——相对误差

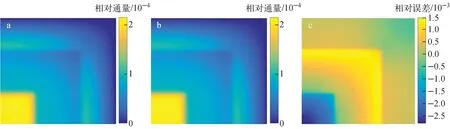
a——全阶模型;b——降阶模型;c——相对误差

2.3 POD基的物理含义

在初步验证了降阶模型的准确性后,对POD基的物理含义进行浅析。将快照矩阵Y与其转置矩阵相乘构成协方差矩阵Σ=YYT,对协方差矩阵特征值分解,即可得到特征值和特征向量,其中前几阶较大的特征值对应的特征向量即为POD基,即POD基来自于样本协方差矩阵的特征值分解。奇异值分解被认为是最佳的分解协方差矩阵的方法之一。对于协方差矩阵Σ,存在分解使得:

Σ=USVT

(23)

式中:U为左奇异矩阵,U=(φ1,φ2,…,φm),其列向量为互相正交的特征向量;S为实对角矩阵,主对角元素为由大到小排列的奇异值,奇异值的平方即特征值。

数学上,U的各列即代表网格点数据的不同变化特征方向,以第1列两个网格点φ1=(k1,k2)T为例,当基向量中两点k1、k2均为正时,代表1点数据变大时,2点数据也变大,即同正向变化;当k1、k2均为负时,代表1点数据变小时,2点数据也变小,即同负向变化;当k1为正、k2为负时,代表1点数据变大时,2点数据反而变小,即相反变化。基向量中每一网格点处数字越大,代表该点处变化程度越强。

每一阶POD基分别代表中子通量场的一种变化模式,根据特征值占比截取前几阶基就是保留中子通量场最主要的变化模式。当只扰动介质1、2的热群扩散系数D2时,计算得ε=99.99%时r1=2、r2=2,分别绘制快群和热群的前两阶基向量的空间分布,如图6、7所示,可以看出,中子通量场的变化主要是由两种变化模式组成的。

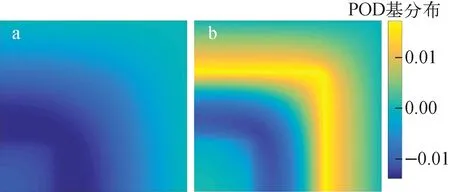
a——1阶;b——2阶

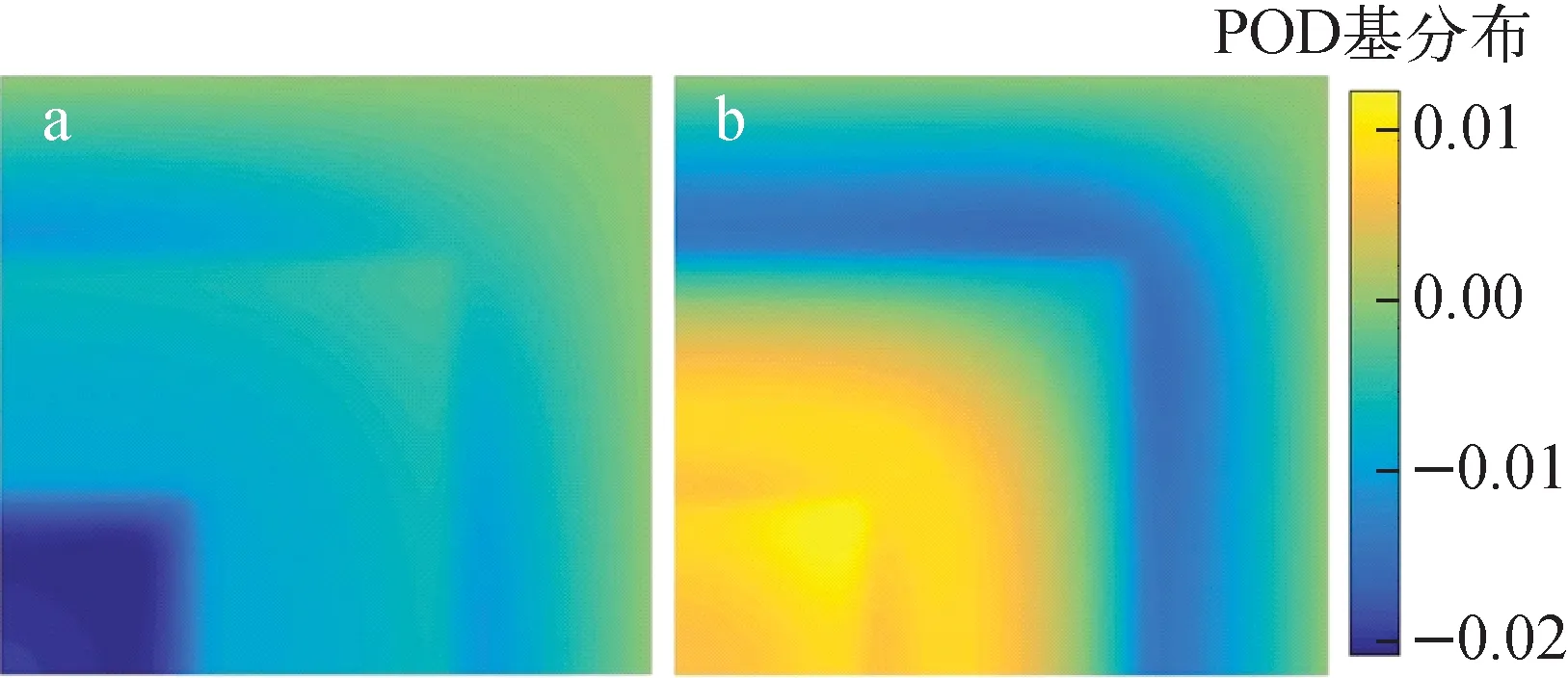
a——1阶;b——2阶

快群第1种变化模式如图6a所示,表明了中子通量的一种同负向变化特征,即同时减小的特征,这种变化的影响效果从内侧3介质区向外,先由弱变强,再由强变弱,越靠近反应堆边缘,影响效果越趋于零。即随着介质1、2的热群扩散系数的增大,整体中子通量均有所减小,尤其是介质1、2所在区域通量减小更多,越靠近边缘,减小程度越趋于零。

快群第2种变化模式如图6b所示,有两个区域具有明显相反的变化特征,介质1、2所在区域为同负向变化,而反应堆边缘3介质区与1、2介质区交界处呈同正向变化特征,内侧3介质区和边缘3介质区的影响效果趋于零。即随着介质1、2的热群扩散系数的增大,1、2介质区通量均有所减小,而边缘3介质区与1、2介质区交界处通量均相应增加。

综合两种变化模式来看,随着扩散系数增大,最主要的变化特征是整体通量减小,而更细节的变化则是1、2介质区通量减小,交界处的通量增大。而当扰动全部14个输入参数时,计算得ε=99.99%时r1=2、r2=2,绘制快群和热群前两阶基向量空间分布如图8、9所示,与图6、7对比可发现,扰动参数量不同时所得基向量分布不同,即中子通量场的变化模式不同。

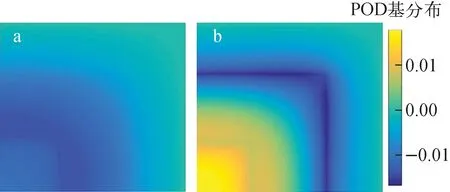
a——1阶;b——2阶

a——1阶;b——2阶

2.4 不确定性分析

为研究降阶模型在提高不确定性计算速度方面的潜力,进行如下测试:令所有参数服从多元正态分布,样本均值为基准题给出的参数值,标准差是参考值的20%,在扰动范围内用简单随机抽样(SRS)和拉丁超立方抽样(LHS)分别采样1 000个样本点,选择10～100个样本点来构建降阶模型,其余900个样本点作测试点,分别进行全阶与降阶计算。

绘制LHS样本量为100的全阶与降阶keff的分位数-分位数图(Q-Q图),如图10所示。由图10可见,全阶与降阶计算的keff分布一致性较强。其中全阶计算时间为47 631.15 s,降阶计算时间(包含基向量生成时间)为5 468.10 s,降阶计算时间仅占全阶计算时间的11.48%。

图10 全阶与降阶keff的Q-Q图

两种抽样方法下不同样本量全阶与降阶keff计算结果列于表2、3。可以发现,随着样本量的增加,keff的数学期望偏差基本稳步下降,样本量为100时,LHS下全阶与降阶的数学期望偏差为1 pcm,属于较小误差;相同样本量时LHS下数学期望偏差小于SRS;另外随着样本量增加,降阶计算相对于全阶计算的时间占比逐渐增加。

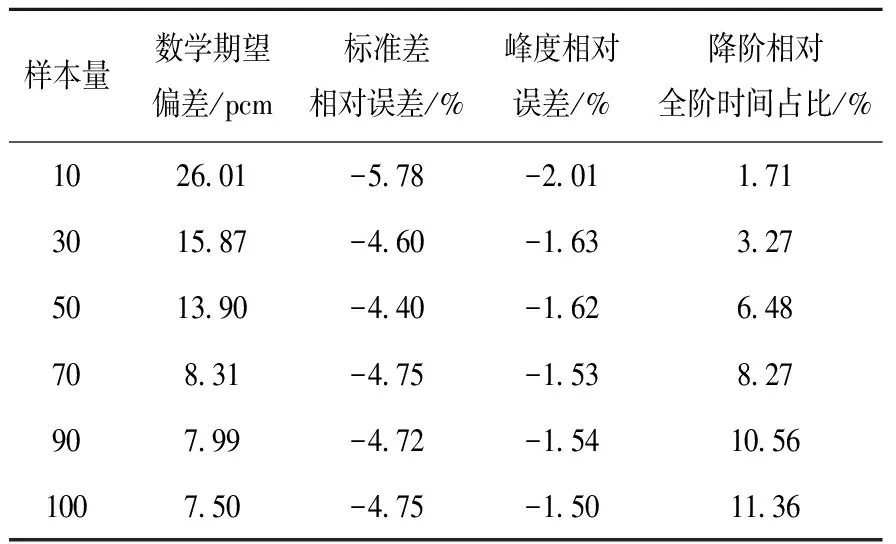
表2 SRS不同样本量全阶与降阶keff计算结果

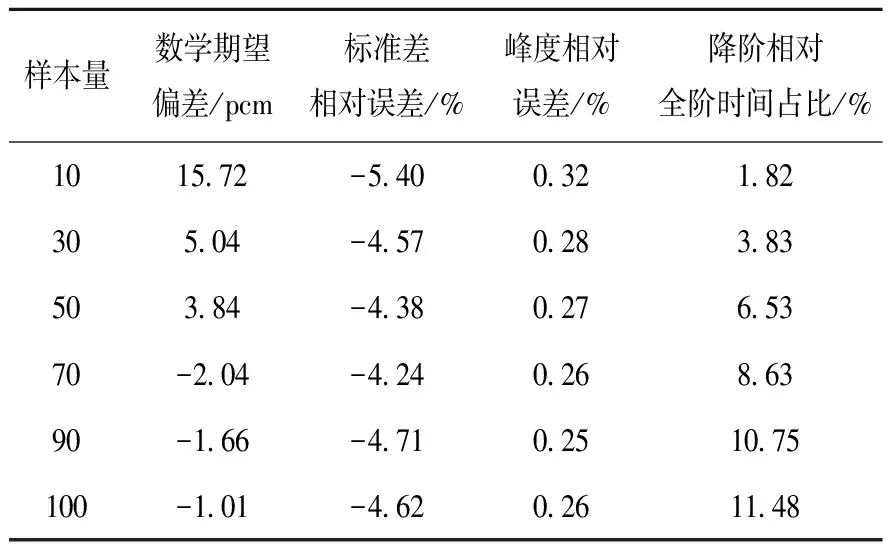
表3 LHS不同样本量全阶与降阶keff计算结果

不同抽样方式将得到不同的样本空间,在相同样本量下,LHS能够提供更为准确的代理模型,既能够使样本均衡地覆盖输入参数的分布区间,而且即使在样本数量较少的情况下,也能够对输入参数的不确定度进行准确合理的表征。在相同样本量下,基于LHS和SRS的降阶模型的不确定性分析结果都能与全阶不确定性分析结果具有较小误差,但相较而言,LHS结果的误差更小。因此,从TWIGL基准题测试结果来看,在POD-Galerkin降阶建模中,相同样本量下,LHS方法更建议采用。

3 结论

本文利用POD-Galerkin方法构建出一种针对稳态二维两群中子扩散问题的物理驱动式降阶模型,并用自主编写的程序成功实施了全阶与降阶模型的计算。根据TWIGL二维两群稳态基准题进行了数值测试,并对其进行了不确定性分析,数值结果如下。

1) 本文构建的降阶模型能够在保证计算精度的前提下,较快地完成中子通量及本征值的求解,降阶模型keff计算结果与基准解偏差为1 pcm,单次运算降阶模型的计算时间仅占全阶的1.02%。

2) 在不确定性分析方面,该降阶模型与全阶模型计算出的keff属于同一分布,且降阶与全阶的数学期望、标准差和峰度具有较小误差;将降阶模型构造所需的全阶模型计算时间考虑在内,降阶不确定性分析计算时间占全阶的11.48%,充分展现了降阶模型在减少不确定性分析计算时长方面的较大潜力。

3) 在相同样本量下,基于LHS和SRS的降阶模型的不确定性分析结果都能与全阶不确定性分析结果具有较小误差,但LHS的结果误差更小。因此在POD-Galerkin降阶建模中,相同样本量下,LHS方法更建议采用。

基于本文对降阶模型应用于中子扩散特征值问题的不确定性分析研究,下一步的工作可以包括:在中子输运问题上推广POD-Galerkin模型降阶方法,以提高中子输运计算效率;在更多输入参数扰动下,考虑参数之间的相关性,采用更高效的抽样方法获得质量更高的样本空间,进一步减小降阶模型与全阶模型的计算误差。