入渗Richards方程Laplace变换步骤中原函数敛散性的讨论
朱悦璐,王义成
(1.南昌工程学院 水利与生态工程学院,江西 南昌 330099;2.中国水利水电科学研究院,北京 100038)
1 研究背景
如何求土壤水分入渗方程的解析解,一直以来是地下水动力学、土壤水动力学以及非饱和入渗理论中的研究热点[1-3],现有的土壤水分入渗方程类型已有很多[4],以Richards方程为例[5],这些微分方程的显示表达式都具有高度非线性,这种非线性包含两个方面:其一是微分方程本身非线性,其二是方程中主要参数非线性(例如非饱和渗透系数K(θ)、非饱和扩散系数D(θ)都是含水率θ、深度z、时间t的非线性函数[6-7]),这导致入渗方程精确的解析解不易求解,很多情况下甚至不能求解。
目前,最常见的处理手段即为采用各种“变换”对入渗方程进行化简,例如Laplace变换[8]、Boltzmann变换[9]、最小作用原理变分变换等[10];这些变换化简的实质,都是一种线性化方案,即通过损失一定的方程精度,来换取实际工程中可以接受的近似解、半解析解[11]。但回顾文献容易发现[12-14],既往学者和工程技术人员,或因为学科背景所限,在采用各种线性化手段时,往往会忽略其前置的数学条件,例如在应用最广泛的Laplace变换线性化Richards方程中,对于变换的前提,即当t→∞时,原函数发散速度不超过指数函数这一问题,历史文献均未进行讨论,研究者皆默认原函数θ(z,t)满足该条件或直接认为原函数收敛。这种做法在大多数的工程案例中是正确的,但在理论上却可能存在反例。
非饱和入渗过程中,含水率θ(z,t)是深度和时间的函数,一般情况下,当z增加时,θ减小,当t增加时,θ增大,如图1(a)所示;但在理论上可能存在这样的曲线,即某种极端的条件下,含水率曲线的函数式不收敛甚至发散速度较快,即在数学上表现为,二元函数θ(z,t)的值随t、z的增大而增大,如图1(b)所示;这会造成传统Laplace变换解在表达式上看似合理但与实际工程不符的情况,此时虽然存在数值解,但由于函数θ(z,t)的快速发散性,Laplace变换的前提已不存在,所化简的线性方程已不适用,即便能求解出某具体数值,也已失去了物理意义。
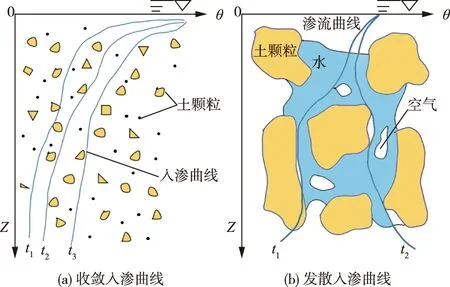
图1 水在不同土质、土壤结构中入渗曲线Fig.1 Water infiltration curve in different soil texture and soil structure
基于此,本文针对非饱和入渗Richards方程Laplace线性变换方案,提出先通过试验,初步拟合可能出现的含水率曲线形态,再利用数学手段判断含水率曲线敛散性,最终确定是否能进行化简变换等3个步骤。从数学计算上完善非饱和土力学理论,从机理上明确化简后的方程,是否能代表入渗曲线最真实形态,并给出不适合拉普拉斯变换的极端工况,通过反例说明本研究在实际工程中的意义和必要性。
2 Richards入渗方程的Laplace变换

(1)
式中:θ0为边界土体含水率;θi为初始土体含水率;t为入渗时间。在式(1)中以θ(z,t)为原函数的Laplace变换为[15]:
(2)
根据Laplace变换性质可得式(3)[16-17]:
(3)
对式(2)第一个等号两边求z的二阶偏导数可得式(4):
(4)
(5)
对于式(5),在数学上已有成熟的解法求得解析解,具体求解步骤见相关数学教材或工程手册[18],本文不再赘述。其解为:
(6)
这样即求出Richards入渗方程经过Laplace变换后的近似入渗曲线θ(z,t),由于erfc(·)函数值不超过1[19],结合θ0、θi定义和运算规则,易得式(6)值恒小于1,含水率计算结果收敛。
2.2 经典变换存在的问题以上讨论了经典变换后入渗方程有形如式(6)的近似解,并知道由式(6)中高斯误差函数的值域,可约束含水率计算结果收敛。但事实上,在实际工程中,入渗曲线θ(z,t)是否收敛在事先是未知的,而上述步骤的实质是,在式(2)右端积分符号内,研究者事先默认θ(z,t)是连续且收敛的,以确保后续运算,而由于二阶线性常系数非齐次微分方程解的固定性,总能得出形如式(6)解的形式,这在物理上相当于用式(6)这种唯一的曲线形态,来拟合所有可能出现的入渗情况,显然,这种做法在数学上并不严谨。
因此本文认为,在进行Laplace变换之前,需进行先验试验,估计某种土样在实际入渗过程中曲线的初步形态,并判断其敛散性,只有确定式(2)中的先验θ(z,t)函数发散速度慢于Laplace变换条件所规定的指数函数时,才能应用Laplace变换对方程进行线性化,其结果用式(6)拟合才是具有物理意义的。以下小节,本文将针对这一问题进行讨论。
3 几种常见的入渗曲线敛散性判断
比较不同函数发散程度的快慢,有多种数学方案,对于本研究的实际问题,含水率函数值恒大于零,因此可采用“作比取极限法”进行判断[20]:任取两函数f(t)、g(t),当t→∞时,若lim(f(t)/g(t))→∞,则f(t)发散速度快于g(t);若lim(f(t)/g(t))→0,则f(t)发散速度慢于g(t)。
3.1 多项式形态入渗曲线敛散性当θ(z,t)曲线具有多项式形态时,以三次多项式为例,其标准方程为:
θ(z,t)=a1z+a2z2+a3z3+b1t+b2t2+b3t3+c1zt2+c2z2t+c3zt+d
(7)
Laplace变换性质表明,要式(2)成立,需有θ(z,t)≤Heβt,其中H、β为常数,这等价于证明t→∞时,θ(z,t)发散速度慢于Heβt。显然对于式(7)当t→∞时,上述命题成立,此时Laplace解满足变换条件。在这种情况下,应用Laplace变换将入渗方程线性化,并求形如式(6)的近似解是可行的。
3.2 指数形态入渗曲线的敛散性当θ(z,t)具有指数函数形态时,一种常见的入渗方程表达式为:
θ(z,t)=zNt
(8)
式中N为常数。在实际入渗过程中,若z由工程条件限制取常数时,易知当t→∞时,zNt与Heβt具有同阶敛散性,因此,当入渗深度固定时,指数形态入渗曲线发散速度不会超过Heβt,该种情况亦可用Laplace变换化简方程。
3.3 幂指数形态入渗曲线的敛散性若在某些条件下,深度z持续变化,式(8)由指数函数转化为幂指数函数(此时z,t均为自变量),当z→∞,t→∞时,有:

(9)
这表明入渗曲线θ(z,t)发散速度快于Heβt,此时,式(2)Laplace变换最右边等号的积分不收敛,因此变换不能成立,在这种情况下,不能用Laplace变换将Richards方程线性化,因为其解已失去物理意义。
4 反例及对比
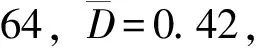

表1 线性化Laplace变换解
将表1计算结果绘制成θ~z函数曲线,如图2所示。该曲线是一簇下凹的函数图形,表示随深度增加,含水率减少,同一深度时,随入渗时间增加,含水率增大。以图中蓝色竖线为分隔,在计算时间内,线性化方程计算结果显示,入渗深度约为15 cm,在z>15 cm区域,含水率为初始含水率0.037,这表明入渗尚未到达该区域。在很多工程案例中,该种形态的入渗曲线经常出现[21-23],这一计算结果“似乎”并无问题。

图2 线性化方程解的入渗曲线Fig.2 Infiltration curve of linearized equation solution
采用同样数据,以算例中实际入渗曲线θ(z,t)=z0.8t代入计算,其结果如图3所示,由于幂指数函数增长过快,图3采用单对数坐标系以便考察,但这并不影响函数的增减性;可以看出,在计算时间内,θ(z,t)函数值随着z,t增加而增加,所有深度均为渗透区,该结果同时也表明,这种极端情况在数学上客观存在。

图3 实际入渗曲线Fig. 3 Actual infiltration curve
为更直观展示上述结果,将线性化方程计算结果和原方程计算结果绘制在三维坐标系θ-z-t中,如图4、图5所示;此时可以清晰的看出,两种情况下,含水率入渗曲面随z、t的变化,呈现相反的凹凸性,这表明,此时无论采用何种方式提高线性化方程式(6)本身计算精度,都已不能有效模拟含水率变化情况,而需要采用其他方法;造成这一现象的数学本质是传统计算方案将非饱和入渗问题化简为一个泛定方程,进而将这类方程又转化为仅与初始条件和边界条件有关的定解问题,而这种不包含渗流场本身信息的微分方程,在某些应用场合存在理论瑕疵。

图5 三维坐标下实际入渗曲线Fig. 5 Actual infiltration curve in 3-dimensional coordinates
上述反例即可证明,Laplace变换化简Richards方程并非适用于所有情况,事实上,在实际工程中,由于土壤性质、孔隙结构以及工程条件的不同,真实非饱和入渗曲线形态差异很大,所对应入渗曲线方程,在数学上能满足严格收敛条件的亦是少数,因此在进行化简变换前,本文所提出的原函数敛散性判断,不论在数学上,还是物理上都十分必要。
5 结论
本研究对非饱和入渗Richards方程的Laplace变换过程中,原函数的敛散性进行了讨论,并得出以下结论:
(1)Laplace变换存在性定理,在非饱和土力学中仍然适用,凡在变换过程中,直接默认原函数收敛或其发散速度小于Heβt的方案,在数学上都不严谨。
(2)在实际工程中,入渗曲线θ(z,t)具有多项式形式、指数形式时,原函数发散速度都小于Heβt,可用化简后的线性化方程求解入渗曲线。入渗曲线若具有幂指数形式,则原函数发散速度快于Heβt,此时Laplace变换积分发散,该变换不成立,因此需用其他方法进行求解。
(3)凡是先验试验中,含水率曲线θ(z,t)的发散速度大于Heβt的,Laplace线性化求解方案均不成立,本文中的反例有效验证了这一结论。

