解析几何八大典型易错点的纠正与剖析
■广东省惠州仲恺中学 陈伟流
解析几何是高中数学几何与代数主线中的重要内容,其内容涵盖点、直线、曲线等多种基本概念,涉及对斜率、长度、面积等多种几何量的求解,在直线与直线、直线与曲线、曲线与曲线的位置关系情境中考查同学们对基本方法、基本思想的有效掌握及灵活应用。但在实际学习中,不少同学却在基本概念、方法技能、解题思维等方面出现理解偏差、考虑不周、思维定式等不良现象,远未达到深度理解并有效掌握的本质性要求。为此,笔者以解析几何中八大典型易错点为例,在错解纠正剖析的基础上,进一步点拨相关题型的求解方法,旨在促进同学们对基本概念、方法技能及解题思维能有更本质、更全面的认知理解,从而促进高考备考中的提质增效。
一、斜率与倾斜角关系辨识不清
剖析:没有正确认识直线的斜率与倾斜角的关系,认为y=tan α在(0,π)上是递增函数,出现思维定式的误判。
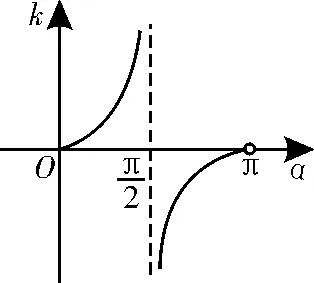
图1
点拨:对于直线斜率与倾斜角的关系判断或范围求解问题,要用函数思想、数形结合思想等进行指导解题,确保思维的严密性。
二、平行关系判断中忽略充分性验证
例2已知直线x+2ay-1=0 与直线(a-2)x-ay+2=0平行,则a=( )。
错解:由两直线平行得-a=2a(a-2),解得a=0或。故选C。
剖析:应用两直线的平行关系进行必要性判断,最后忽略了充分性验证,产生增根。
正解:由两直线平行得所以。故选D。
点拨:对于直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,则l1∥l2⇔A1B2=A2B1且A1C2≠A2C1;l1⊥l2⇔A1A2+B1B2=0,由此可知平行关系判断中需进行A1C2≠A2C1的充分性验证,避免两直线重复产生增根,垂直关系中则无需验证。
三、忽略直线方程的适用范围,产生漏解
例3求过点(2,4)且在坐标轴上的截距之和为0的直线方程。
错解:设直线方程为,因为直线过点(2,4),所以,解得a=-2,代入直线方程得x-y+2=0。
剖析:截距式方程只适用于截距不为0和不平行于坐标轴的情形,错解中没有考虑截距为0的情形,导致漏解。
正解:当直线的截距均为0时,直线过原点,易得其方程为y=2x;当直线的截距均不为0时,同错解得直线方程为x-y+2=0。综上可得,所求的直线方程为2x-y=0或x-y+2=0。
点拨:在截距相等(反)、截距绝对值相等或截距成倍数的情境中应用截距式方程,应考虑截距为0 及不为0 的特殊与一般的情形。同样的,两点式方程也不适用于斜率为0和斜率不存在的情形,所以应用直线方程时应充分考虑方程的适用范畴,避免因思维不严密而出现漏解。
四、忽略圆方程成立的必要条件
例4若过点A(4,2)可以作两条直线与圆C:(x-3m)2+(y-4m)2=25(m+4)2相切,则点A在圆C的____(填“外部”“内部”“上面”),实数m的取值范围是_____。
错解:易知点A(4,2)在圆C的外部,代入圆C的方程可得(4-3m)2+(2-4m)2>25(m+4)2,解得。
剖析:忽略圆的半径需大于0 的必要条件,产生思维漏洞。
正解:易知点A(4,2)在圆C的外部,代入圆C的方程得(4-3m)2+(2-4m)2>25(m+4)2,且25(m+4)2>0,解得m<且m≠-4,故实数m的取值范围是。
点拨:对于圆的标准方程(x-a)2+(y-b)2=r2中的r>0 及一般方程x2+y2+Dx+Ey+F=0中的Dx+Ey+F>0的必要条件是解题过程中容易忽略的点。
五、轨迹方程求解中忽略几何图形存在的必要条件
例5在△ABC中,内角A,B,C的对边分别为a,b,c,若a,c,b依次成等差数列,且a>c>b,|AB|=2,求顶点C的轨迹方程。
错解:由a,c,b依次成等差数列得a+b=2c=4,即|CA|+|CB|=4>|AB|,故顶点C的轨迹为椭圆,如图2,以AB的中点为原点建立平面直角坐标系,则易求得椭圆方程为。
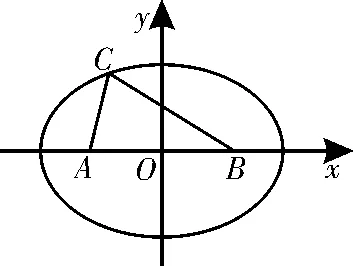
图2
剖析:求解中忽略了边长的大小关系及A,B,C三点不共线的前提条件。
正解:因为a>b,所以|CB|>|CA|,故轨迹只能取椭圆在y轴左侧的部分,且A,B,C三点不共线,需挖去椭圆的左顶点(-2,0),故顶点C的轨迹方程为(-2<x<0)。
点拨:在求解动点轨迹方程时,除了要注意圆锥曲线成立的前提条件,还需注意动点在某些特殊位置是否与题意的几何条件产生矛盾,从而明晰变量的取值范围,培养思维的严密性。
六、对直线与圆锥曲线的位置关系理解有偏差
例6已知过点(0,3)的直线与双曲线有唯一公共点,则这样的直线有_____条。
错解:设所求直线方程为y=kx+3,联消去y整理得(1-2k2)x2-12kx-20=0,由Δ=(-12k)2+80(1-2k2)=0得,故满足题意的直线有2条。
剖析:错解中混淆了直线与双曲线相切和有一个公共点的逻辑关系。
正解:当直线与双曲线的渐近线平行时,其方程为,分别与双曲线的一支有一个公共点,符合题意;当直线与渐近线不平行时,设其方程为,同错解得,故满足题意的直线有4条。
点拨:在判断直线与圆锥曲线的关系位置中,若直线与封闭曲线(圆及椭圆)相切,则二者只有一个公共点;若直线与双曲线只有一个交点,则直线与曲线相切或平行于双曲线的一条渐近线。
七、忽略根的判别式的适用范围
例7已知圆(x-a)2+y2=4与抛物线y2=6x没有公共点,求a的取值范围。
错解:联立消去y整理得x2+(6-2a)x+a2-4=0,可知方程无实数解,故Δ=(6-2a)2-4(a2-4)<0,解得,故a的取值范围为。
剖析:根的判别式只适用于直线与曲线的位置关系的判断,并不适用于曲线与曲线的位置关系的判断,错解忽略了根的判别式的适用范围。
正解:易知圆的圆心为(a,0),半径为2,抛物线的顶点为(0,0)。当圆与抛物线内切时,a=2;当圆与抛物线外切时,a=-2。要使两者无交点,则需a>2或a<-2,故a的取值范围为(-∞,-2)∪(2,+∞)。
点拨:在判断两个曲线的位置关系时,可通过几何图形的临界状态(曲线相切),以形助数找到参数的临界值,再对图形进行动态分析,从而进一步明确参数的取值范围。
八、运算路径、方法不恰当,导致运算受阻或产生困难
例8已知椭圆C:,过点D(1,0)且不过点E(2,1)的直线l与椭圆C交于A,B两点,直线AE与直线x=3交于点M。试判断直线BM与直线DE的位置关系,并说明理由。
剖析:在错解中忽略了直线斜率存在的前提条件,同时没有遵循先特殊后一般的求解逻辑,一旦后续求解出现卡壳就会使解题停滞不前,继续引发解题失败。
当直线AB的斜率存在时,同错解得kBM=1=kDE,故BM∥DE。
综上可得,直线BM与直线DE平行。
点拨:在解析几何的定值、定点、位置关系判断等问题的求解中,可优先通过直线斜率不存在(或斜率为0)等特殊条件对问题进行必要性的结论探索,再通过一般性证明结论的完整性,以减少运算方向的不明确性和阻碍性,提升运算效益。

