勤思善研探过程砥砺深耕提能力

陕西省西安市高新第三中学(710075) 吕二动

在中高考改革与教学创新的今天,越来越多中高考试题呈现出回归教材的趋势,课本知识是学习的基础和根本,对课本知识进行适当的研究和拓展,会有意想不到的收获. 不仅有利于拓宽数学视野,深化对数学知识的认知和理解,还可以提升学生解决问题的能力,培养学生的数学核心素养.

引例如图1, 点A在反比例函数xy= 2 上, 点B在反比例函数xy= -1 上,且∆AOB是等边三角形,求∆AOB的面积.

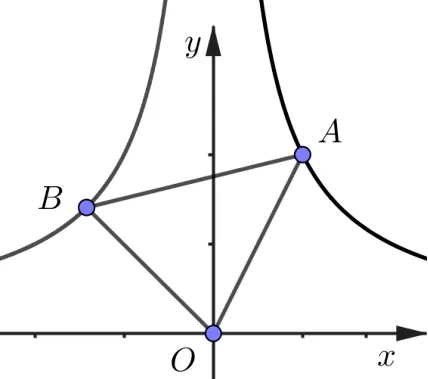
图1

笔者在一本教辅资料看到此题,感觉此题具有丰富的内涵和研究价值,便对该题做了深入研讨,具体如下:

一、介绍两个引理

引理1 平行四边形ABCD内接三角形DEF,则

证明设∠A=α,α∈(0◦,180◦),AB=a,AD=b,AE=x,CF=y. 则BE=a-x,BF=b-y,S.ABCD=absinα. 因为所以BE=所以

所以

所以

即

因为S.ABCD=S∆ADE+S∆CDF+S∆BEF+S∆DEF. 所以=(S∆ADE+S∆DCF+S∆BEF)2-4S∆ADE·S∆DCF.

引理2矩形ABCD内接正三角形CEF,则S∆AEF=S∆CDE+S∆BCF.

证法1如图2. 设EC= 2a, ∠DCE=θ, 则∠BCF= 30◦-θ, ∠AEF= 30◦+θ, 从而S∆CDE=2a2sinθcosθ=a2sin 2θ. 同理S∆BCF=a2sin(60◦-2θ),S∆AEF=a2sin(60◦+2θ). 故

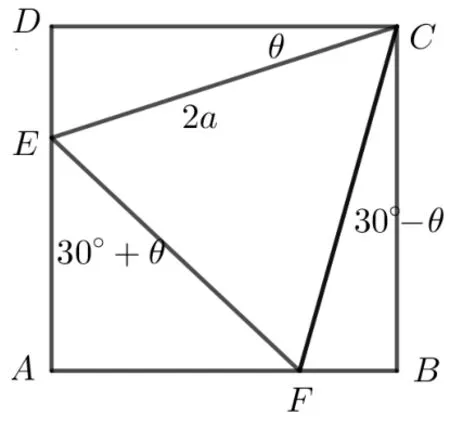
图2

即S∆CDE+S∆BCF=S∆AEF.

证法2如图3, 设EC= 2a, ∠DCE=θ, 则∠BCF= 30◦-θ, ∠AEF= 30◦+θ, 从而S∆CDE=2a2sinθcosθ=a2sin 2θ. 同理S∆BCF=a2sin(60◦-2θ),S∆AEF=a2sin(60◦+2θ). 作CT= 2a,∠TCE= 2θ, 则∠FIC=60◦+2θ. 从而

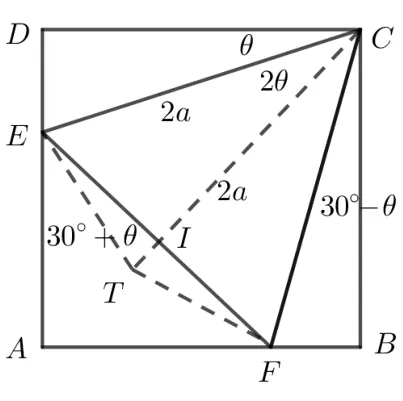
图3

即S∆CDE+S∆BCF=S∆AEF.

证法3如图4,设AB=a,BC=b,BF=x,DE=y,则AF=a-x,AE=b-y, 且(a-x)2+ (b-y)2=x2+b2=y2+a2,从而

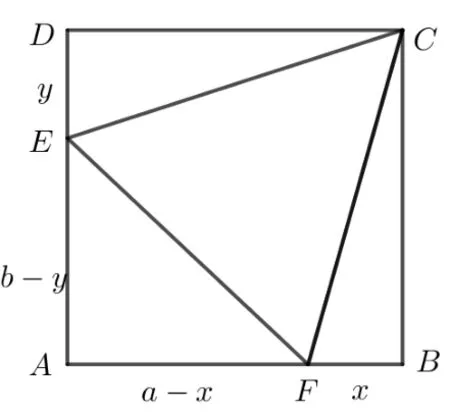
图4

①×a2- ②×b2得a2x2-b2y2-2(ax+by)(a2-b2)=0,即(ax+by)(ax-by-2a2+2b2)=0,所以ax-by-2a2+2b2=0.

将by代入①中得到:b2-2ax+4a2-4b2-2ax+x2=0,即(x-2a)2=3b2,x=同理所以因为

证法4如图5, 作∆CDE∽= ∆CFI, 则∠ICB=∠IFA= 30◦, 由S∆CIF+S∆CBF=S∆BIF+S∆CBI得即2ay+2bx=ab+xy,即ay+bx= (a-x)(b-y), 从而S∆BCF+S∆CDE=S∆AEF.

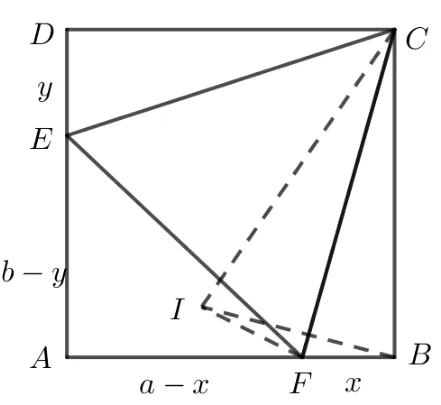
图5

二、性质研究

结论1已知点A在反比例函数xy=k1(k1>0)上,点B在反比例函数xy=k2(k2< 0)上,且∆AOB是等边三角形,则∆AOB的面积是

解析如图6,根据引理2 可得

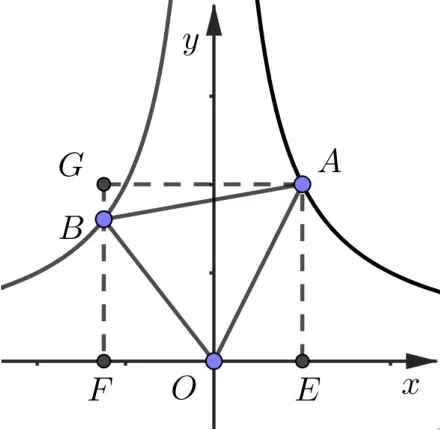
图6

再由引理1 可得

注前面引例的问题就会迎刃而解,即为

结论2已知直线y=kx+t(k≠ 0) 与反比例函数xy=m(m≠ 0) 交于两点, 连接OA,OB, 且∆AOB是等边三角形, 则m=

太史公曰：诗有之：“高山仰止，景行行止。”虽不能至，然心乡往之。余读孔氏书，想见其为人。鲁，观仲尼庙堂车服礼器，诸生以时习礼其家，余祗回留之不能去云。天下君王至于贤人众矣，当时则荣，没则已焉。孔子布衣，传十余世，学者宗之。自天子王侯，中国言“六艺”者折中于夫子，可谓至圣矣！

证明如图7, 设一次函数y=kx+t与x轴,y轴相交于D(0,t) 两点. 由反比例函数性质可知AD=BC, 又OA=OB, ∠OAD= ∠OBC, 所以∆OAD∽= ∆OBC, 所以OC=OD. 故kAB= -1 即化简得ab=m,又因为OA=AB,所以,即a2-4ab+b2=0. 又因为b>a,解得所以所以所以

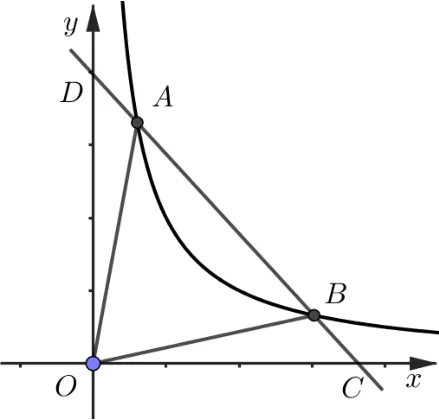
图7

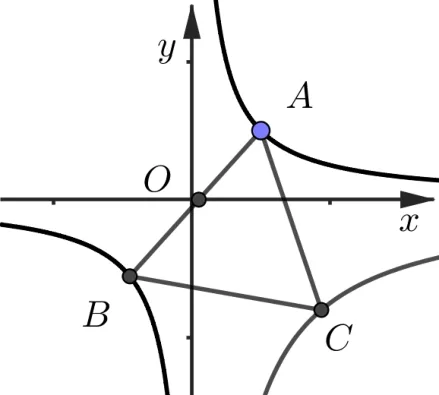
图8

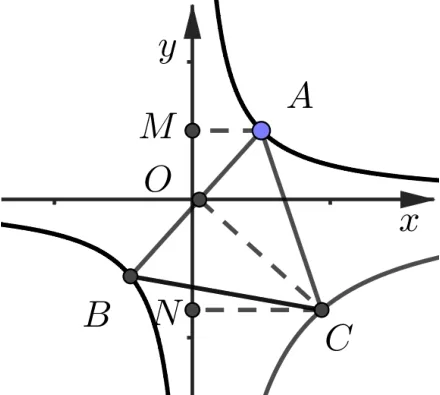
图9

结论3已知直线y=kx与反比例函数xy=k1相交于A,B两点, 点C在反比例函数xy=k2(k1·k2< 0)上, 且∆ABC是等边三角形, 则k2= -3k1,S∆ABC=

证明连接OC, 分别过点A,C作AM⊥y轴、CN⊥y轴, 交y轴于点M,N. 因为∆ABC是等边三角形, 所以OC⊥AB, 且因为∠OMA= ∠CNO=90◦, 且∠AOM= ∠OCN, 所以∆OMA∽∆CNO, 又所以S∆ONC= 3S∆OMA即k2= -3k1. 设A(xA,yA),联立,所以

故k2=-3k1,

结论4设P(x0,y0)是反比例函数xy=k(k≠ 0)上任意一点,过点P(x0,y0)作其切线l分别交x轴,y轴于A,B两点,则点P是线段AB的中点,且∆AOB的面积为定值,即S∆AOB=2|k|.

证明由xy=k(k≠ 0) 得, 求导得, 则过点P(x0,y0) 的切线l的方程为,令x=0 时,,令y=0时,,则xA= 2x0,yB= 2y0,所以点P是线段AB的中点,S∆AOB= 2|x0y0| = 2|k|,故点P是线段AB的中点, 且∆AOB的面积为定值, 即S∆AOB=2|k|.

结论5设P(x0,y0)是对勾函数上任意一点, 过点P(x0,y0) 作其切线l分别交y轴, 直线y=ax于A,B两点,则点P是线段AB的中点,且∆AOB的面积为定值,即S∆AOB=2|b|.

结论6设P(x0,y0)是双曲线= 1(a> 0,b>0)上任意一点,过点P(x0,y0)作双曲线的切线l分别交渐近线于A,B两点,则点P是线段AB的中点,且∆AOB的面积为定值,即S∆AOB=ab.

注结论5、6 的具体证明过程可仿照结论4 的证明,留给有兴趣的读者!

三、变式研究

结论7直线y=kx(k> 0) 与反比例函数xy=k1(k1> 0) 相交于A,B两点, 点C在反比例函数xy=k2(k2<0),则三角形ABC的面积的最小值为解得

证明设A(x0,y0),C(xC,yC), 则B(-x0,-y0), 由

点C到直线kx-y= 0 的距离为又因为xcyc=k2,所以

结论8直线y=kx(k>a)与函数0,b> 0) 相交于A,B两点, 点C在函数y=mx+则三角形ABC的面积的最小值为

结论9直线y=kx(k> 0) 与反比例函数xy=k1(k1>0)相交于A,B两点,点C在圆:x2+y2=r2(r>0),则三角形ABC的面积的最大值为

结论10直线y=kx(k> 0) 与反比例函数xy=k1(k1> 0) 相交于A,B两点, 点C在椭圆:1(a>b> 0), 则三角形ABC的面积的最大值为√

结论11直线y=kx(k>a)与函数0,b> 0) 相交于A,B两点, 点C在椭圆:1(a>_b> 0), 则三角形ABC的面积的最大值为√

由于篇幅有限,具体证明可仿照结论7 的证明过程.

通过对引例的研究和拓展发现,我们对典型试题应从不同角度去思考,挖掘试题的本质,从而更好地解决新的问题,推理出新的结论,叶圣陶先生说过“教材无非是个例子”,我们应该充分利用好这个“例子”,才能将其思想和方法内化为学生的数学能力和数学素养.