对一类基本不等式错解问题引发的深度探究

江苏省淮阴中学教育集团淮安市新淮高级中学(223001) 王恩普

在复习基本不等式求最值这类题型时,有部分学生在解决问题的过程中出现了一些错误的解法,但是却不认为有问题,亦或是感觉有问题又不知错在哪里,很是困扰,笔者对此进行了深入的探究.

1 错解呈现

例1已知a>0,b>0,a+b=1,求的最小值.

错解过程由a> 0,b> 0 知:当且仅当时取等号,由可得:此时则所求最小值为6.

我们知道答案显然是错的,那么错在哪里呢?

2 类比示错

为了解决这样的问题,先从一个最基本的求最值问题开始研究:

例2已知x>0,求的最小值.

分析由基本不等式易知: 当x>0 时,4,当且即当即x=2 时取等号,即的最小值为4.

但若类比本文开头的解题逻辑, 也可以这样处理: 当x>0 时,当且仅当时即时取等号,此时可得即的最小值为

还可以再换一种方案来处理: 当x> 0 时,当且仅当时即x= 1 时取等号,此时可得即的最小值为5.

如果继续按照类似的方案来处理,将得到更多不同的结果,此时学生也意识到根据基本不等式建立不等关系,得到取等条件,再根据取等条件求出的x值回代求最值的思路是存在问题的,文首的双变量求最值问题亦是如此,但是到底错在哪里呢?

3 理性释疑

参考上述错解过程的做法, 当x> 0 时,仅仅表示这个不等式是恒成立的, 此时,记x> 0,则不等式表示的几何意义是: 在y轴的右侧,f(x)的图象恒在g(x)图象的上方(可以有交点),如图1,而取等号的条件对应的x则表示f(x)的图象与g(x)图象相切时的切点的横坐标,换言之,若按照这样的方法求出的最值,其结果是由左边配凑后的式子决定的,而将每改变一种配凑形式,将得到不同的函数g(x),同时切点的位置也随之变化,而其横坐标可以取像前文中的1,,亦或是大于0 的每一个数.

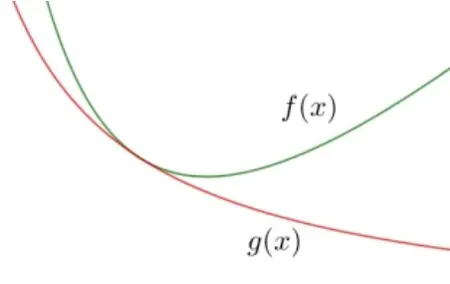
图1

结合开头展示的正确过程: 由x> 0,根据基本不等式知:当且仅当即x= 2 时取等号,由此可知只有当x=2 的时候f(x)取得最小值,那么此时的过程为何正确呢? 继续来看图象,如图2,此时g(x) = 4,由于g(x)的图象是一条与y轴垂直的直线,同时f(x)的图象恒在g(x)图象的上方,取等号的条件则对应着f(x)的图象与g(x)图象的切点处,即x= 2 时f(x)有最小值,此时,也就说明了使用基本不等式求最值时不等号的右侧应该是个定值,至此,我们不仅找到了错误的根源,也明白了应该如何去处理.

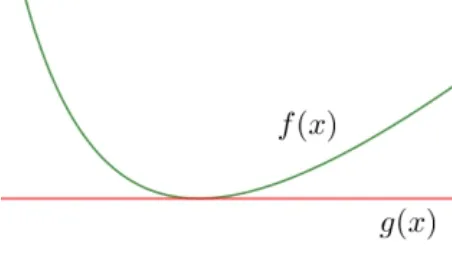
图2

文章开头给出借助基本不等式求双变量类型最值问题,其错解原因也是一样的,其实这也是平时提炼出的利用基本不等式求最值时,要注意“一正二定三相等”的原则,“一正”保证了基本不等式可用, 而“二定”则是指使用基本不等式时,不等式的一侧应为常数(不含变量),得到了可能产生的最值,“三相等”则是验证了最值的存在性,而文首出现的错误则是没有真正理解“二定”的原则.

4 巩固提升

当从根本上理解了错误的原因之后,接下来通过一组题来看下此类问题应如何处理.

例3已知a>b>0,a+b=1,求的最小值.

解由a>b>0 知a-b>0,且有(a-b)+2b=1,则

评注过程中在上乘以(a-b)+2b,目的是为了配凑出这两个积为定值的代数式,进而求出最值.

例4已知a>b>0,a+b=1,求的最小值.

解由a>0,b>0,a+b=1 知:≥2+1=3,当且仅当时取等号,此时由a+b=1 可得,则的最小值为3.

评注过程中的1 用a+b来代换,其目的也是为了配凑出这一对积为定值的代数式,从而使得问题得到解决.

例5已知a>b>0,且求ab的最小值.

解由a>b> 0 知当且仅当时取等号,而则有,化简可得ab≥8,由与ab=8 可得a=2,b=4,则ab的最小值为8.

评注本题中虽然开头运用基本不等式建立的不等关系的右边不是定值,但是此时结合题中的条件可以得到ab≥8,也是符合前文研究的基本不等式求最值的情况,只是稍微间接了一点,此时得到了两个不等关系,需要验证两个不等式成立的公共条件是否成立.

例6已知a>b>0,求的最小值.

解由题知当且仅当a4=1即a=1 时取等号,由a>b>0 知当且仅当时取等号, 由a= 1,可得,a=1,的最小值为

评注同例5,过程中运用了两次基本不等式才使得不等式的一侧为常数,则需要去进一步验证两次使用基本不等式取等的条件能否同时成立.

5 思想升华

除了利用基本不等式可以直接解决一些最值问题,还可以借助于这种求最值的思想来帮助我们解决一些较为复杂的问题,而且有着事半功倍的效果.

例7函数f(x)=xex-ax+b的图象在x=0 处的切线方程为:y=-x+1.

(1)求a和b的值;

(2)若f(x)满足: 当x> 0 时,f(x) ≥lnx-x+m,求实数m的取值范围.

解(1)a=2,b=1. (过程略)

(2)分析 常规的做法是构造函数直接求最值,但是此时求最值的过程会涉及到隐零点代换等方法, 过程相对复杂,对学生的推理能力要求比较高,而下面的解法则较为简洁.

由f(x) ≥lnx-x+m知,m≤xex-x-lnx+1,由ex≥x+1(当且仅当x=0 时取等号)知

当且仅当x+lnx=0 时取等号,令g(x)=x+lnx(x>0),则则g(x) =x+ lnx在定义域上单调递增, 又< 0,g(e) = e + 1 > 0,则存在x0使得g(x0) = 0, 即x+ lnx= 0 有解, 即有(xex-x-lnx+1)min=2,则m≤2.

评注题中的求最值过程采用了放缩法,正是基本不等式法求最值思想的本质体现,而放缩法之所以可行,正是因为建构的不等式的一侧是定值,而后面的过程则体现了取等这个另一重要的环节,完美的展现了方法与思想的迁移.

往往一个错误的解法都是有其原因的,有时只是根据提供的解答进行纠正,强行入驻大脑,也许只是过眼云烟,因此,我们有必要去探究这样的解答错了没有,错在哪里,为什么错, 对此进行充分研究之后, 才真正的走进深度学习, 当然,在此基础之上,能将掌握的知识,方法,思想进行发展,迁移,会将更好的提升自身的创新能力.