对一道分式型最值问题的探究

广东省云浮市云浮中学(527300) 成永深

题目(《数学教学》2023 年第2 期问题1173 为) 当x> 1,y> 2,z> 3 时, 求的最小值.

解法1易证当x> 1,y> 2,z> 3 时,事实上,有

解法2设s=a+b+c,a,b,c,s>0,则

取等条件为a+b+c=6,2a=b,3b=2c,c=3a即

解法3设a,b,c>0,由均值不等式得

当a= 1,b= 2,c= 3,即时取等号.

解法4由已知条件结合柯西不等式和配方法得

解法5由柯西不等式结合基本不等式得

二 变式拓展

2.1 变式1当x>1,y>2 时,求

的最小值.

解如图1 所示, 在直线l上依次取点P,O,Q, 使得OP= 1,OQ= 2,AP垂直于PQ且OA=x,BQ垂直于PQ且OB=y, 四边形APQA′为矩形. 则AP=所以

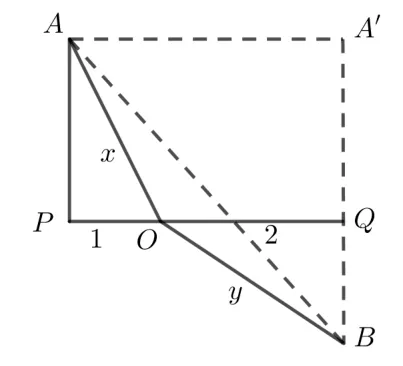
图1

取等条件为A,O,B三点共线且A′B= 3, 即y=即时取等号.

变式2当x>1,y>2,z>4 时,求

的最小值.

解设a,b,c>0,由代数变形结合均值不等式得

2.2 推广

推广1已知a1>b1,a2>b2且a1,a2为变量,b1,b2为正常量,则的最小值为2(b1+b2).

证明设则

当a1=a+1,a2=b+2,b1= 1,b2= 2 时,则问题就是2018 奥地利数学奥林匹克不等式题:

已知a,b∈R+,则

推广2已知a1>b1,a2>b2,··· ,an>bn且a1,a2,··· ,an为变量, {bn} 为正项等差数列或等比数列, 记数列{bn}的前n项和为sn,则

的最小值为2sn.

证明设,则

2.3 几个结论

结论1若bn=n(n∈N∗),则

的最小值为n(n+1).

结论2若bn=n+1(n∈N∗),则

的最小值为n(n+3).

结论3若bn=n+k(n∈N∗,k=0,1,2,···),则

的最小值为n(n+2k+1).

结论4若bn=2n-1(n∈N+),则

的最小值为2(2n-1).

当a1=d1+b1,a2=d2+b2,··· ,an=dn+bn,bn=n(n∈N∗),则

的最小值为n(n+1),取等号条件为

该问题便是2018 奥地利数学奥林匹克不等式题的推广.