克列尔公式及关联公式的应用与思考

云南师范大学数学学院(650500) 丰魁 何月 张勇

四面体作为空间中最基本的几何体,其体积及外接球问题一直是高频考点之一,常作为压轴小题出现,对学生的空间想象、逻辑推理、数学运算等能力都有较高要求. 通常采用综合几何法或向量法求解,但在一些情况下,空间点、线、面的位置关系较难确定,此时若能辅以恰当公式解之,可大大减少思维量.

1 克列尔(A.L.Crelle)公式

对任意四面体,其体积V和外接球半径R满足

要证明此公式,我们先推导以下引理:

引理对任意四面体, 其体积其中,S1,S2为以a为公共棱的两个面的面积,θ为这两个面所成的二面角.

引理的证明如图1,AH为∆ACD在DC边上的高,AE为三棱锥A-BCD的高,连接EH,则∠AHE=θ即为二面角A-DC-B的平面角,记∆BDC,∆ACD的面积分别为S1,S2. 则由解得

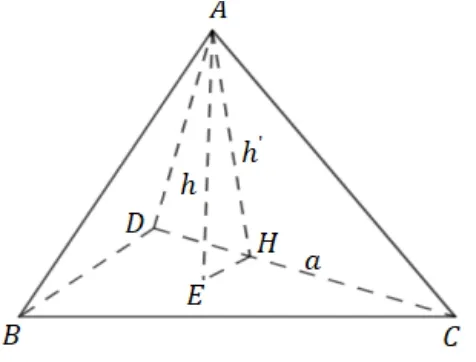
图1

证明设四面体的各棱长如图2,过顶点A作外接球的切面α,过B作平面β//平面ACD,过D作平面γ//平面ABC,则平面α,β,ABC,ABD构成四面体ABD1C1,平面α,γ,ABC,ADC构成四面体ADB2C2. 在平面ABC上,由于AC1在外接球的切面上,所以AC1与∆ABC的外接圆(外接球与面ABC的交线) 相切, 从而∠C1AB= ∠ACB.又BC1//AC(平行平面β,ACD与平面ABC的交线平行, 所以∠ABC1= ∠BAC, 于是∆ABC1//∆CAB, 得同理,又C1D1//C2A,C1A//C2B2, 所以∆C1AD1//∆C2B2A, 得将∆AC1D1放大倍,就得到一个边长为aa1,bb1,cc1的三角形.

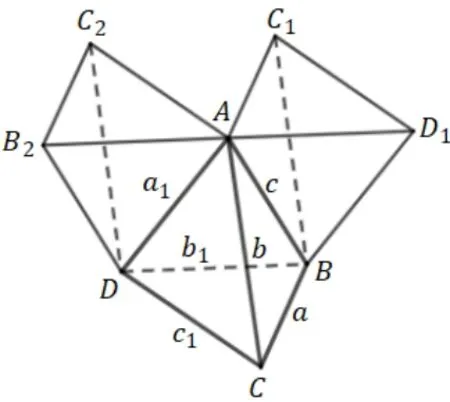
图2

过A作外接球的直径,设B在这直径上的射影为B′,则由射影定理,有. 由于AB′⊥切面α,所以它就是B到切面α的距离,因此,这里再由引理中的公式,可得

例1(2023 年华南师范大学附属中学高三测试第7题) 在四面体ABCD中, 若AB=CD=AC=BD=则四面体外接球的表面积为()

解如图3,取BC,AD的中点分别为N,H, 连接AN,DN,NH, 易知BC⊥AN,BC⊥DN, 故NC,BN分别为四面体ACDN,ABDN的高, 且两体积相等. 由三角形全等知AN=DN,故NH⊥AD,由勾股定理得

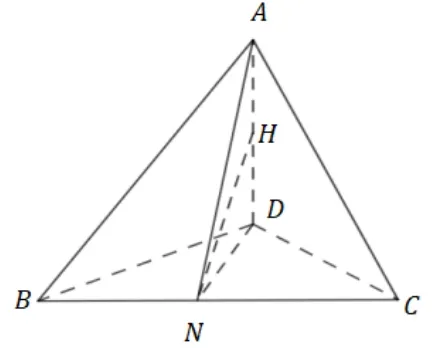
图3

评注该题中体积除了结合几何关系由求解外, 亦可由求解, 其中∠AND即为A-BC-D的二面角,cos ∠AND易由边长关系由余弦定理解出,也可以∆BCD为底,AN·sin ∠AND作为四面体的高求解. 值得一提的是,该问题原题题干中已经给出了克列尔公式,本文为了便于叙述作了适当删减. 应注意到,立体几何与高等数学中的空间解析几何的一些概念定理相融合,综合考查学生信息提取、知识的灵活运用能力的信息类题型也是高考模拟热点之一,对于此类问题,要克服畏难情绪,耐心阅读并理解题意,联想已学知识结合新信息解决问题.

2 二面角公式(三射线定理)

对于克列尔公式的运用,题干往往会以直接或间接的方式给出四面体的6 条棱长, 关键在于求四面体的体积, 例1中四面体体积相对来说容易求解,但若棱长不具备特殊关系,四面体的高和二面角往往较难确定,因此我们可以继续推导二面角和体积更为一般的关系式.

如图4,α和β是两相交平面, 所交直线上有一点P,PA,PB是从P点出发的两条射线,在两射线上分别取H,N, 分别过H,N向两面所交直线PC作垂线, 这里取H,N两点满足两垂足相交于同一点M, 记∠APB=θ,∠APC=θ1,∠BPC=θ2,二面角A-PC-B为φ,则有

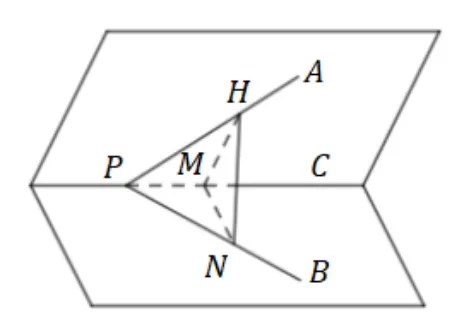
图4

证明因为HM⊥PC,NM⊥PC, 易得PH=MN=PMtanθ2,在∆HPN,∆HMN中,由余弦定理得

由①= ②解得cosθ= cosθ1cosθ2+sinθ1sinθ2cosφ,命题得证.

在上文图1 中,令∠ACB=θ,∠ACD=θ1,∠BCD=θ2,BC=c,AC=b. 至此任意四面体体积公式可进一步化为

该公式的各余弦值可以通过已知边长利用余弦定理得到,结合克列尔公式使用更具一般性. 当然,还可进一步往下推导,利用余弦定理解出各余弦值代入上式,就可以得到一个用6 条棱长表示的体积公式,但运算繁琐复杂,且在初等数学中适用性不强,较为简洁的推导涉及高等数学知识,因此本文不作说明,可参考文献[2-3].

例2在三棱锥P-ABC中,AC=PA=PC= 3,AB= 4,BC= 5,二面角P-AC-B的平面角的大小为30◦,则三棱锥P-ABC的体积为____,外接球的表面积为____.

解记∠PCB=θ,由勾股定理知AC2+AB2=BC2,故AB⊥BC, 所以且∠PCA= 60◦, 由二面角公式可得故,由体积公式可得

在∆PCB中, 由余弦定理可得PB2=BC2+PC2-2BC·PCcosθ, 解得由克列尔公式得p=故

评注对于上述涉及二面角和外接求半径的模型,还有一个运算量更小且对题干已知量要求更少的公式,即在任意四面体ABCD中,若BC= 2a,二面角A-BC-D的平面角为φ,∠BAC=α,∠BDC=β,则四面体外接球的半径

证明可参考文献[4].

在例2 中,根据该公式

3 线面角公式

除了上述的二面角与体积密切相关,若已知线面角,则体积也容易求出,反过来,根据上述由二面角对体积公式的推导, 可以得到如下的一个线面角公式: 在上述图1 中, 记AC与平面BCD所成角为β, 根据线面角的定义及上文叙述,即sinβ= sinθ1sinθ, 该式子通常被称为三正弦定理, 进一步,将二面角换成上文推导出来的结果,还可以得到

例3(2023 年全国乙卷理科数学第9 题)已知∆ABC为等腰直角三角形,AB为斜边,∆ABD为等边三角形,若二面角C-AB-D为150◦,则直线CD与平面ABC所成角的正切值为()

解易知∠ABD= 60◦,∠CBA= 45◦,设∠CBD=θ,由二面角公式可得,解得, 不妨设AC=BC=a, 则AB=AD=由余弦定理得CD2=BD2+BC2-2BD·BCcosθ,解得,故

易知∠BCD= ∠ACD, 且∠ACB= 90◦, 记线面角为φ,∠BCD=∠ACD=α,∠ACB=90◦=β,故

评注事实上,由题干中特殊的等腰和等边三角形,本例的二面角也容易作出,故可直接用余弦定理求出CD的长再使用线面角公式,由例1、例3 可以看出,即便在完全套用公式的情况下,适当的进行一些几何分析,也有助于简化运算.

4 公式应用建议

立体几何综合考查的是空间想象与几何分析的能力,二级公式、定理并非是解题的“万能药剂”, 因此, 切忌死记硬背,生搬硬套,比如在共顶点的三条棱两两垂直的四面体外接球模型中,若强行套用克列尔公式,运算量极大,反而适得其反. 再比如上述例3 中,若能结合线段长度关系,作出二面角,便很容易作出线面角,问题可以更为高效的解决,上述采用线面角公式并非考场上的最佳选择. 归根结底,几何定理、空间位置关系的基本方法和基本思想仍是解题之根,不能完全用公式的“算”替代几何分析的“想”,当然,若能在平时解题过程中,注意到各个具体题目的共性,从特殊到一般,运用综合几何法或者向量法推导出上述公式, 作为辅助解题的“利器”,这不单有助于提高解题效率,还能够使几何直观的素养更上一个阶层.