二参数逻辑斯蒂模型项目参数的估计精度*

杜文久 周 娟 李洪波

(1西南大学数学与统计学院,重庆 400715)(2重庆市教育考试院,重庆 401147)

1 引言

教育和心理测验都是由相应的测验项目组成,测验项目质量的好坏直接决定了测验的质量。精确掌握每个测验项目区分度参数和难度参数的相关信息,对于教育和心理测验项目的筛选以及测验的编制具有重要的参考价值(涂冬波,蔡艳,戴海琦,丁树良,2011)。另外,计算机化自适应测验(

Computerized Adaptive Testing

,CAT)自20世纪70年代早期被引入测验领域,而实施 CAT需要一个优质、大型的题库,同时题库还需要不断更新(陈平,辛涛,2011),淘汰一些质量不够好的试题,加入一些新的试题。可见,对项目参数进行准确估计就非常重要(Maij-de Meij,Kelderman,&van der Flier,2008)。

目前,国内外对项目参数估计精度的研究,大部分是基于在已知项目参数真值的情况下,运用各种参数估计方法(常用的参数估计方法有极大似然法、贝叶斯方法、MCMC方法等)产生新的估计值,再和真值进行偏度(BIAS)和均方根差(RMSE)的比较,从而说明该种估计方法的有效性(Liang &Wells,2009;Finch,2010) 。均方根差RMSE、Bias的计算公式分别为：

其中

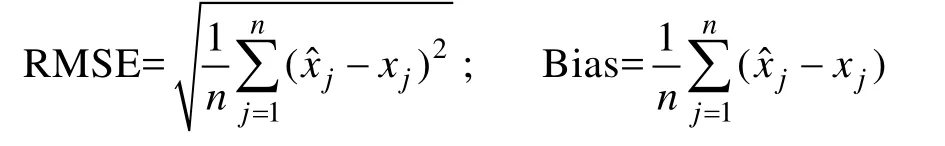
x

表示第

j

个项目参数(a或 b)的真值,

x

表示第

j

个项目参数的估计值,

n

表示重复试验的次数。通过公式可看出,均方根差反映的是

n

次重复试验中项目参数真值与项目参数估计值之间的平均偏差大小;偏差的值反映了项目参数真值与参数估计值之间偏差的平均。这种方法只能得出每个参数真值的估计误差,无法反映不同的参数之间的估计误差是如何随着参数真值的变化而变化的。

为了弥补这些缺陷,本文尝试从项目参数信息函数的角度出发,研究二参数逻辑斯蒂模型项目参数的估计精度。目前,国内外主要研究能力参数的信息函数,而对于项目参数的信息函数还没有人研究,本文尝试填补这一空缺。同时还探索了影响估计精度的主要因素有哪些,以及这些因素是怎样影响项目参数的估计精度的。希望通过本文的研究,能够为题库编制者和测验编制者提供一些有价值的参考信息。

2 研究方法

2.1 项目参数的极大似然估计

首先,假设能力参数已知,通过讨论二参数逻辑斯蒂模型项目参数(

a

,

b

)的极大似然估计,从而获得项目参数估计值的置信区间。设

X

,

X

,… ,

X

为

N

个能力分别为

θ

,

θ

,… ,

θ

的被试在某个二级评分项目上的得分,如果被试

j

在项目上答对,则

X

=1,否则

X

=0。于是根据被试

j

在项目上的反应可得似然函数：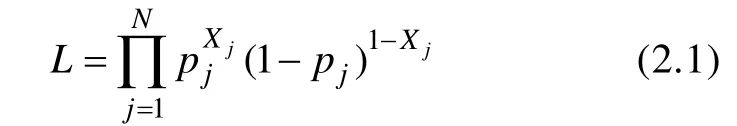

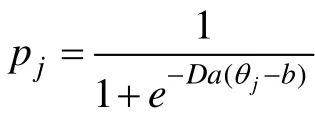
由(2.1)式两边取对数,再分别对

a

,

b

求导,除以

N

后令其等于零,得：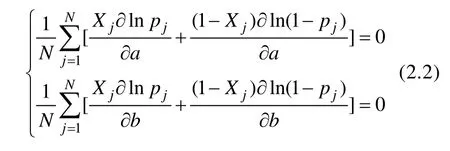

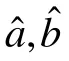
其中,(

a

,

b

)表示向量(

a

,

b

)的转置,

I

(

a

,

b

)表示矩阵

I

(

a

,

b

)的逆,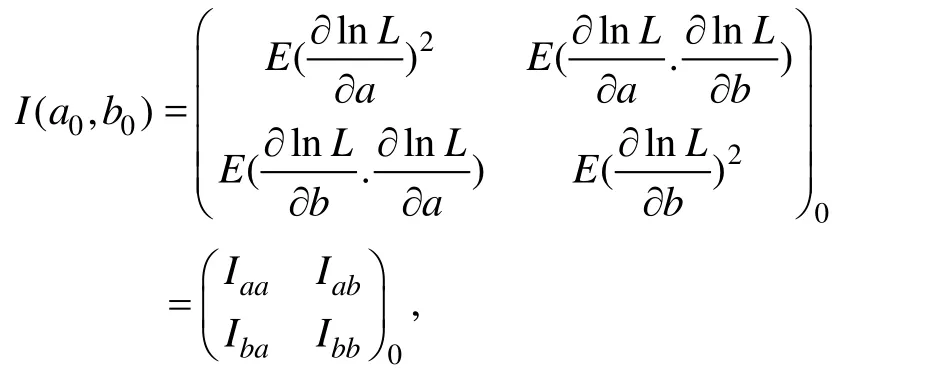

下标“0”表示将表达式中的

a

,

b

用

a

,

b

代替。根据Lord(1980)的计算(漆书青,戴海崎,1992;Hambleton &Swaminathan,1985),

I

、

I

(

I

=

I

)、

I

的表达式如表1。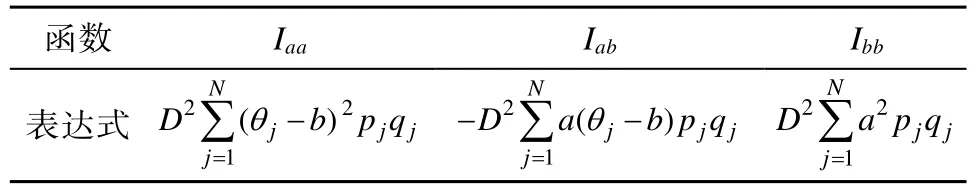

表1 Iaa、Iab(Iba= Iab)、Ibb的表达式

由上式不难发现：

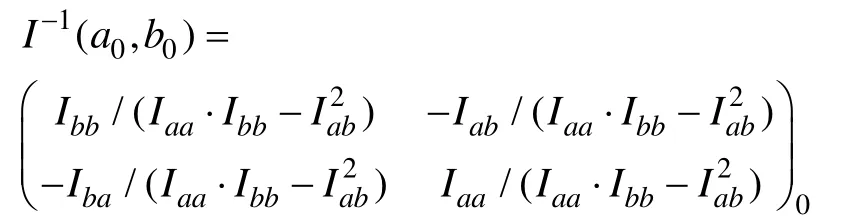
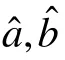
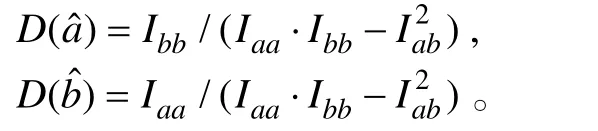
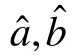
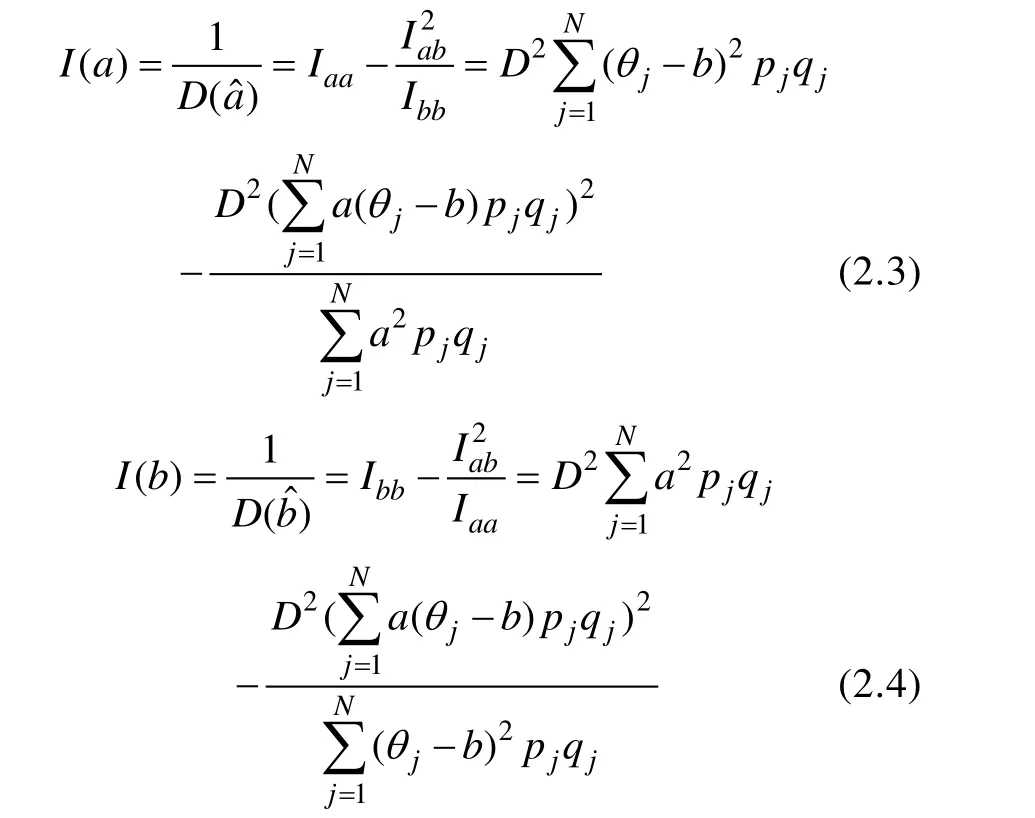
I

(

a

)、

I

(

b

)值越大,参数

a

、

b

估计值的方差越小,从而估计值也就越精确;反之,

I

(

a

)、

I

(

b

)值越小,估计值的方差就越大。因此,可用项目参数

a

、

b

的估计信息函数,描述参数

a

、

b

的估计精度。

2.2 参数估计值的置信区间

给定置信水平α=0.05,由正态分布表可查得双侧分位值

μ

=1.96,于是在 95%的概率意义下,

a

,

b

的置信区间分别为：

结合参数

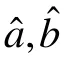
a

,

b

的信息函数和其估计值的置信区间,就能对项目参数的估计精度进行研究。

3 实证研究

为了探明被试的样本容量和能力分布对项目参数的估计精度的影响,按以下方法和实验设计进行模拟研究：

(1)假设被试能力参数已知,被试的能力分布取两种情形：标准正态分布

N

(0,1)和均匀分布

U

[−3,+3];

(2)被试样本容量为3个水平：100人,500人,1000人;

(3)以区分度参数

a

为横坐标,难度参数

b

为纵坐标,项目参数

a

,

b

的估计信息函数

I

(

a

),

I

(

b

)分别为垂直坐标绘制各种情形下

I

(

a

),

I

(

b

)的三维图像。(4)所有随机生成数据和作图过程均由Matlab2009(王沫然,2009)程序实现。为制图方便,区分度参数

a

的取值范围确定为[0,3],难度参数b的取值范围确定为[−3,3]。

根据上述设计,本实验共有2× 3×2=12种不同的类别。

3.1 区分度参数a的估计信息函数

分别随机产生服从标准正态分布

N

(0,1)和均匀分布U[−3 ,+3]的100个、500个、1000个被试的能力参数值,根据公式(2.3),画出不同情形下(2×3)

I

(

a

)的三维图形,如表2。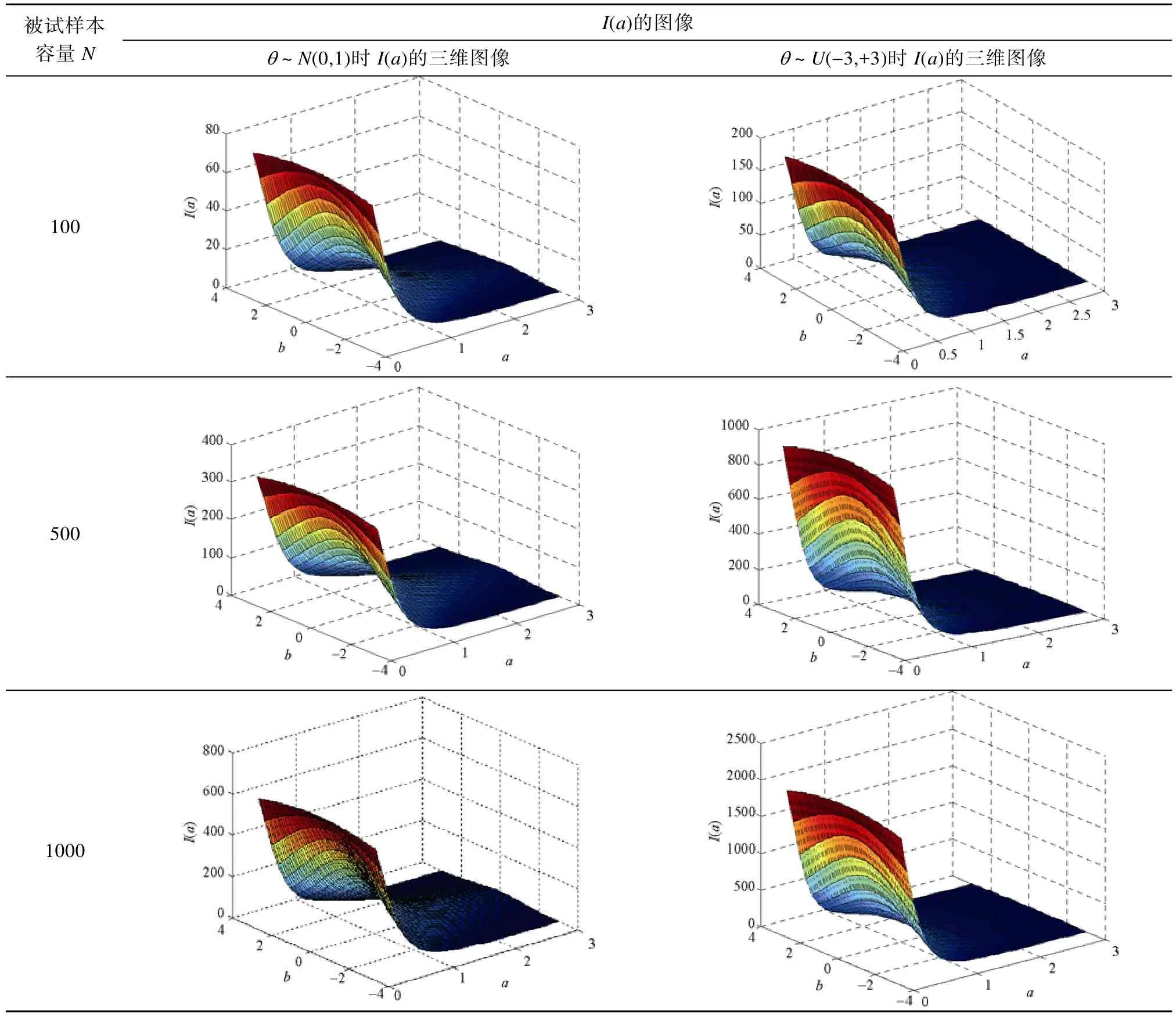

表2 不同情形下区分度参数a的估计信息函数I(a)的三维图像

由表2可知：区分度参数

a

的信息函数同时受到参数

a

、参数

b

和被试样本容量的影响。首先讨论样本容量的影响：比如,当能力参数θ～

N

(0,1)时,在

a

=1,

b

=0附近,被试样本容量从100人、500人增加到1000人时,

I

(

a

)值从20、100增加到约200。可见,增加被试的样本容量,能有效提高区分度参数

a

的信息量,从而提高参数

a

的估计精度。当固定参数

b

和被试样本容量时,区分度参数

a

的信息量受

a

参数真值本身的影响很大。如当能力参数θ～

N

(0,1),样本容量为1000,

b

=0时,在区分度参数

a

的真值

a

=0.5附近,

a

的信息量约为450,而随着

a

真值的增大,

a

的信息量迅速减小。当

b

=0,

a

>3时,

a

的信息量迅速减小到接近于零。上述结果表明,如果测试项目的区分度参数

a

的真值过大,即使被试样本容量很大,其区分度参数

a

的估计精度也不高。参数

a

的信息量不仅受到被试样本和参数

a

的真值的影响,同时还受到难度参数

b

的真值的影响。图1是被试样本容量为 1000人,能力参数

θ

～

N

(0,1)时区分度参数

a

的估计信息函数

I

(

a

)的三维图像在

b

轴和

I

(

a

)轴所在平面的正投影。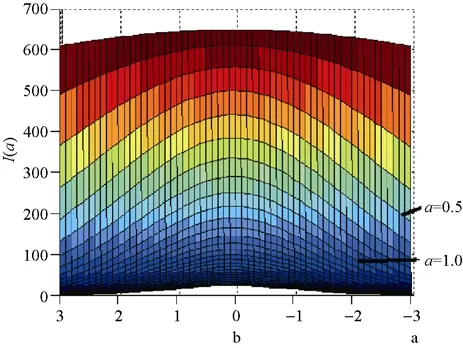

图1 I(a)在b轴和I(a)轴平面的正投影图

由图1可知,对任意给定的

a

值,

I

(

a

)的图像都是一条钟形曲线。例如,假设参数

a

的真值为

a

=0.5时,在

b

=0处,

I

(

a

)取得最大值。随着参数

b

渐渐远离零点,

I

(

a

)值也逐渐减小。这与表2中图形所呈现的结论是一致的,即

b

=0时,

I

(

a

)的三维图像有一条明显隆起的脊线,而脊线上的点就是

I

(

a

)在不同

a

参数位置时的最大值点。另外,当

a

=1时,尽管

I

(

a

)的图像仍然是一条钟形曲线,但该曲线整体上比

a

=0.5时的

I

(

a

)图像降低了很多。也就是说,当参数

a

值增大时,测验所提供的参数

a

的信息量迅速减少,即对参数

a

的估计精度迅速降低。这与前面提到的随着

a

真值的增大,

a

的信息量减小的结论也是保持一致的。从表2中可看到,被试能力参数呈均匀分布与被试能力参数呈标准正态分布时的估计信息函数

I

(

a

)的图像十分类似,只是在

I

(

a

)图形的陡平程度上有差异。在样本容量相同时,能力分布服从正态分布的的

I

(

a

)的曲线相对于能力分布服从均匀分布的

I

(

a

)的曲线要陡峭。由此可得,被试的能力分布对参数

a

的估计精度有影响。

3.2 难度参数b的估计信息函数

根据公式(2.4),画出不同情形下(2×3)难度参数

I

(

b

)的三维图像,如表3。由表3可知,难度参数

b

的估计信息函数

I

(

b

)的图像与区分度参数的信息函数

I

(

a

)的图像差别很大,而且信息函数

I

(

b

)明显受到被试的能力分布的影响。比如,在样本容量为1000时,若被试的能力分布服从标准正态分布,那么任意给定一个

a

值,如

a

=3,则

I

(

b

)的曲线与正态分布的密度函数曲线非常相似;同样,若被试的能力分布服从均匀分布,则在

a

=3处,

I

(

b

)的曲线也非常类似于均匀分布的曲线。

I

(

a

)、

I

(

b

)的图像与能力分布之间的关系如表4所示。可知,难度参数

b

的信息函数受能力分布的影响很大,相对来说,区分度参数

a

的信息函数受能力分布的影响要小一些。另外从表3中还可得出结论,难度参数

b

的信息函数也受到参数

a

的真值、参数

b

的真值和被试样本容量的影响。(1)参数

b

的信息函数值随着样本容量的增大而增大。(2)参数

b

的真值对估计信息值的影响因能力参数分布的不同而不同。(3)当区分度参数

a

的真值增大时,

b

的信息函数也随之增大。

I

(

b

)与区分度参数

a

之间的关系如图2所示。图2是在样本容量为1000,被试能力分布服从标准状态分布时

I

(

b

)的三维图形在

a

轴和

I

(

b

)轴所在平面的正投影。从图中可看到,在任意给定的

b

值,

I

(

b

)的图像是区分度参数

a

的单调递增曲线,在

a

=0附近,

I

(

b

)取得最小值,

I

(

b

)值随着

a

值的增大而增大。当

b

=1.5时,尽管这时

I

(

b

)的图像仍然是一条单调递增的曲线,但该曲线上的

I

(

b

)值比

b

=0时的

I

(

b

)值小很多。也就是说,随着

b

逐渐的远离零点,

b

的信息量也渐渐减小,当|

b

|>3时,

b

的信息量减小到接近于零。上述结果表明,对于能力分布服从正态分布的情形,在

b

=0附近,测验才能提供最大的

b

参数信息量。如果测试项目的难度参数的绝对值|

b

|过大,即使被试样本容量很大,其难度参数

b

的估计精度也不高。因此,在测验编制或者题库建设中项目不应过于简单或是难。

3.3 a0,b0的置信区间

在题库建设和测验编制中,为了提高测验的质量,人们总希望同时提高项目难度参数和区分度参数的估计精度。通过以上对参数

a

、

b

的信息函数方面的讨论,根据公式(2.5)、公式(2.6),可画出

a

,

b

的置信区间。图3和图4分别为区分度参数

a

和难度参数

b

的 95%的置信区间的三维图像,其中,能力参数服从标准正态分布,被试样本容量为1000。图3的横轴表示区分度参数,纵轴为难度参数,竖轴表示区分度参数

a

的真值,下曲面表示置信区间的左端点曲面,上曲面表示置信区间的右端点曲面,任意作一条与

a

、

b

轴所在平面垂直的直线,直线与两曲面相交部分的线段长度就是区分度参数

a

的真值的置信区间长度,该直线与

a

、

b

坐标平面的交点的横坐标就是

a

的估计值。图4的横轴表示难度参数

b

,纵轴表示区分度参数

a

,其余与图3有类似的解释。1)区分度参数

a

的估计误差由图3可知,在难度参数

b

∈[−2,2]内,对于区分度参数值位于 0—2之间的试题,其对

a

的估计误差约为0.15个单位。例如,假设区分度参数

a

的估计值为 1,那么在 95%的概率意义下,其真值位于区间(0.85,1.15)内。当难度参数

b

∈[−2,2]外时,

a

参数的估计误差迅速增大,例如,当

a

=2.7,

b

=−2.2时,

a

参数的估计误差约为2.5个单位,这样大的估计误差实际上已经没有什么价值。

表3 不同情形下难度参数b的估计信息函数I(b)的三维图像

表4 被试能力分布对I(a)、I(b)的影响(被试样本容量N=1000)

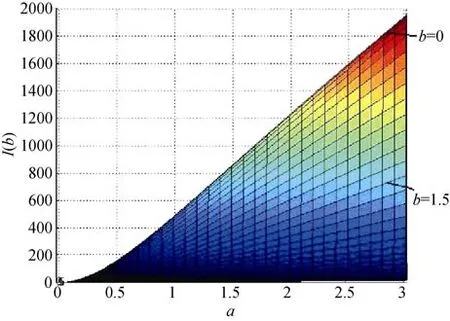
图2 θ ～ N(0,1)时1000个被试下参数b的信息函数投影图

2)难度参数

b

的估计误差由图4可知,在固定参数

a

时,对于难度参数位于−1—1之间的试题,其估计误差约为 0.3个单位。例如,如果项目的难度参数估计值为0,那么在95%的概率意义下,其真值将位于区间(−0.3,0.3)内。当参数

a

变化时,参数b的置信区间也受到参数

a

的影响,在

a

=0=0附近两曲面间的距离相对较大,即

a

值越大,对

b

的估计精度越好。在b=0时对

b

的估计精度最好,|

b

|越大,

I

(

b

)的值逐渐变小,估计精度就越差。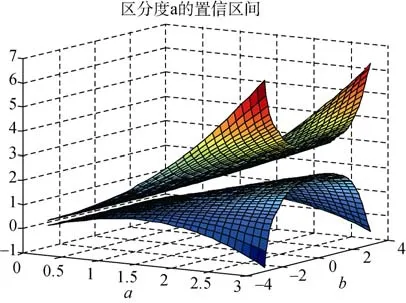

图3 区分度参数a的置信区间

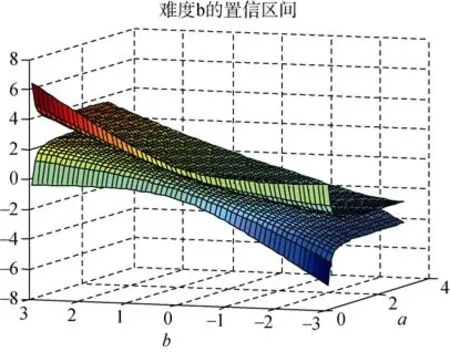
图4 难度参数b的置信区间

4 讨论与结论

本研究定义了二参数 logistic模型项目参数的估计信息函数,并讨论了项目参数的估计精度,给出了参数估计值的置信区间。从本文的讨论可以得到：

在已知被试的能力参数估计项目参数时,对于不同的测验项目,其项目参数的估计误差也不相同;

与采用均方根差方法来估计项目误差的方法相比,借助于项目参数的估计信息函数能够更精确的描述项目参数的估计误差;

(当能力参数已知时)项目参数的估计误差仅与项目有关,而与能力参数无关;

(当能力参数已知时)项目区分度参数

a

与难度参数b的估计精度相互影响,相互制约。项目难度参数b与能力分布的期望值越接近,对b的估计精度越高,同时项目区分度参数

a

越大,b的估计精度越高;对

a

参数而言,

a

越小,对

a

的估计精度越高,同时b的绝对值越小,

a

的估计精度越高。项目参数

a

、b的估计精度还受到被试样本容量和能力分布的影响,样本容量越大,对项目参数的估计越精确。如果被试的能力参数服从标准正态分布,只要样本容量足够大,对位于[−1.5,1.5]之间的项目难度参数 b,都能获得较为满意的估计精度。而对于难度参数b大于1.5的项目,则需要足够多的高能力被试参与测验,否则估计误差会很大。同样,对于低难度的测试项目,要获得理想的估计精度,也需要有足够多的低能力被试参与测验,才能获得满意的估计精度;对于项目的区分度参数

a

,一般情况下,

a

应位于(0.5,2)之间才能获得较好的估计精度,如果

a

真值过大,即使样本容量很大,其估计精度也不理想。

不管是编制测试还是构建题库,掌握每一道题目的性质和信息非常重要。本研究定义的项目参数的信息函数可研究在一次测验中的每个试题在区分度和难度两个指标上分别能给全体被试提供多大的信息(能力信息函数是指一次测验中所有的测验项目能为某特定能力的被试提供多大的信息量)。区分度参数的信息函数可考察一道试题在区分度方面给一组被试提供的信息量。难度参数的信息函数能考察具有特定难度的试题在难度方面能给一组被试提供多大的信息量。结合项目参数的信息函数和估计方差,可以对试题的参数估计精确问题进行更系统的研究,在编制试题时也可根据测试的性质(选拔性、资格性)控制项目参数的信息量。希望上述讨论能够为题库编制者和测验编制者提供一个有价值的参考信息。

Chen,P.,&Xin,T.(2011).Item replenishing in cognitive diagnostic computerized adaptive testing.

Acta Psychologica Sinica,43

(7),836–850.[陈平,辛涛.(2011).认知诊断计算机化自适应测验中的项目增补.

心理学报,43

(7),836–850.]Finch,H.(2010).Item parameter estimation for the MIRT model:Bias and precision of confirmatory factor analysis--based models.

Applied Psychological Measurement

,

34

(1),10–26.Hambleton,R.K.,&Swaminathan,H.(1985).

Item response theory:Principles and applications.

Boston:Kluwer-Nijhoff.Li,X.P.(1997).

Foundation of probability theory.

Beijing,China:Higher Education Press.[李贤平.(1997).

概率论基础

.北京:高等教育出版社.]Liang,T.,&Wells,C.S.(2009).Amodel fit statistic for generalized partial credit model.

Educational and Psychological Measurement,69

(6),913–928.Lord,F.M.(1980).

Applications of item response theory to practical testing problems.

Hillsdale,NJ:Lawrence Erlbaum Associates.Maij-de Meij,A.M.,Kelderman,H.,&van der Flier,H.(2008).Fitting a mixture item response theory model to personality questionnaire data:Characterizing latent classes and investigating possibilities for improving prediction.

Applied Psychological Measurement

,

32

(8),611–631.Mao,S.S.,Cheng,Y.M.,&Pu,X.L.(2004).

Probability theory and mathematical statistics.

Beijing,China:Higher Education Press.[茆诗松,程依明,濮晓龙.(2004).

概率论与数理统计教程

.北京:高等教育出版社.]Qi,S.Q.,&Dai,H.Q.(1992).

Item response theory and its application

.Nanchang,China:Jiangxi Universities and Colleges Press.[漆书青,戴海崎.(1992).

项目反应理论及其应用研究

.南昌:江西高校出版社.]Tu,D.B.,Cai,Y.,Dai,H.Q.,&Ding,S.L.(2011).Parameters estimation of MIRT model and its application in psychological tests.

Acta Psychologica Sinica,43

(11),1329–1340.[涂冬波,蔡艳,戴海琦,丁树良.(2011).多维项目反应理论:参数估计及其在心理测验中的应用.

心理学报,43

(11),1329–1340.]Wang,M.R.(2009).

MATLAB and science compute

(2nd ed).Beijing:Publishing House of Electronics Industry.[王沫然.(2009).

MATLAB与科学计算

(第2版).北京:电子工业出版社.]