从解题策略审视运算错误

☉江南大学附属实验中学 庞彦福

☉江苏省江阴市第一中学 钟珍玖

☉江苏省无锡市蠡园中学 武益燕

对于一个人来说，运算能力是数学能力和数学素养的一种重要体现，对于初中学生来说，运算能力是数学能力的重要体现.不少学生考试的时候都吃过运算错误的亏.数学运算如果不过关，就会直接影响后续内容的学习.数学学习中的运算问题，无论是教师教学还是学生学习都没有特别感觉到有非常“难懂难理解”的地方.对学生来说，在考试时，不“难懂难理解”的运算却时常出错或丢分，这很让数学教师感到“纠结”，也使学习数学的学生非常“纠结”.从数学学习策略角度审视理解解题策略，就是要让学生理解：怎样做、为什么这样做、在什么条件下这样做？解题中不难的运算问题为什么容易出现错误呢？现举几例从解题策略角度剖析其错误产生的原因．

一、对公式法则没有真正理解

问题1 计算：（a+2b-c）（a-2b-c）.

错误类型举例：

生1：把（a+2b-c）（a-2b-c）按照多项式乘以多项式直接展开时，却出现了漏乘“项”的问题.（过程略）

生2：（a+2b-c）（a-2b-c）=［（a+2b）-c］［（a-2b）-c］=（a+2b）2-c2=a2+2ab+b2-c2.

评析：如果生1对多项式乘以多项式的方法和过程很熟练的话，是不应该出现错误的.倘若追根求源查上位知识，就是单项式乘以多项式不够熟练；进一步向上查找，是单项式乘法没有过关；进一步向上查找，又会发现：幂的运算乃至数的运算可能还存在一定的问题.数学运算不是简单的程式化操作与重复，运算的上一步与下一步之间的关系、道理、依据都必须搞清楚弄明白，否则，即使这一步没有“漏项”或出错，也难保下一步还会“幸运”！生2的运算过程显然是通过变形先套用“平方差公式”，再运用“完全平方公式”以达到计算化简的目的.但是，在运用“平方差公式”过程中，对公式的“相同的项”与“相反的项”理解不透，本来原式应该变形为“［（a-c）+2b］［（a-c）-2b］”，却出现了“（a+2b-c）（a-2b-c）=［（a+2b）-c］［（a-2b）-c］”，致使第一步的变形就出现了错误.数学运算开始时错了，就等于走路时方向错误，下面的运算、变形都会随之而错.从解题策略审视该题的解法应该优先选择运用“公式”的方法进行解决，如果想不到或发现不了运用公式等灵活方法时，可以考虑“多项式乘法”，按照多项式乘以多项式的方法展开进行化简也能达到目的.所以，教师在平时教学时应注重公式、法则的形成过程，让学生在具体事例中体会公式、法则的结构特征、使用范围等，强调对公式、法则抽象过程的理解，为准确、熟练、灵活运用公式打下坚实的基础.

二、只知步骤不明算理

错误类型举例：

生1：去分母，得2x+6-1-x=1.（以下略）

生2：去分母，得2x+6-1+x=8.（以下略）

三、运算法则逆用不灵活

问题3 已知3x=5，27y=7，求3x-3y的值.

错误类型举例：

生1：因为3x=5，27y=7，所以3x-3y=3x-33y=3x-27y=5-7=-2.

生2：将27y=7变形为27y=（33）y=7，但是，接下来却找不到进一步解下去的思路.

评析：生1和生2在解决本题的过程中都出现了思维障碍，生1的解答是将幂的指数相减理解成了幂的结果相减，显然是不理解且没有依据的乱写.生2也尝试着将幂的“底数”朝着某个方向转化，但最终还是没有找到解决的办法.如果能逆过来想一想的话，可能就会恍然大悟.幂的指数在什么情况下相减（同底数幂除法）？因此，需要将所求的式子转化成“同底数幂除法”，即3x-3y=3x÷33y，而33y又可以逆用“幂的乘方”变形为：33y=（33）y，进一步朝着题目条件追溯查找，目标越来越明朗，（33）y就是27y，这样问题就迎刃而解了.其实，学生也是知道的，数学的公式、法则往往是可以逆用的，既可以从左到右，也可以从右向左，就是在解决问题的过程中却不能灵活自如地运用起来.从学习策略的角度审视数学解题，学习数学，仅仅靠多训练是不够的，必须做到真正理解和掌握，务必注重解题后的总结、反思与提炼.教师在教学时，不能认为公式、法则的逆用仅仅是把它们的位置进行了置换，方向进行了颠倒.实际上逆用公式、法则是新的思维方式发生了变化，即逆向思维，只有学生顺用公式、法则非常自如时，对公式的结构特征和法则的本质属性深刻理解时才会进行逆用，教师应在夯实学生对公式、法则理解的基础上，加强训练和反思，才能取得教学的实效.

四、没能从通法走向技巧

问题4 已知实数a≠b，且满足a2+3a-7=0，b2+3b-7=0，求a+b的值.

错误类型举例：

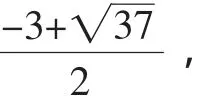
生3：两式相减，可得a2-b2+3a-3b=0，进一步变形得（a-b）（a+b-3）=0，因为a≠b，所以a-b≠0，所以a+b-3=0，即a+b=3.

《义务教育数学课程标准》（2011年版）这样描述：“运算能力主要是指能够根据法则和运算律正确地进行运算的能力．培养运算能力有助于学生理解运算的算理，寻找合理简洁的运算途径解决问题.”据此可概括出运算能力的几个基本特征，即正确、有据、合理、简洁.这也启示我们数学教师，运算不等同于计算，运算能力也并非一种单纯的、孤立的数学能力．它需要正确理解相关知识，辨识分清运算条件，合理选择运算方法，有效设计运算步骤，还要使运算符合算律、算理，并且尽可能简洁地获得运算结果．它是“算”与“思”的结合、操作与思辨的融合．

数学的运算能力是整个数学学习的基础，运算能力是数学能力与数学素养的重要体现．数学不仅要讲推理，更要讲道理，同样数学运算不仅要明算法，更要明算理．算法的每一步做什么具体而明确，前一步和后一步之间有着内在的逻辑关联，不可随意倒置．算法的思维要求学生有条理地思考和演算，问题的解决策略是建构在已经解决的问题之上，一步一个脚印，拾级而上．算理是算法的思维本质，算法是算理的外在表现形式，是避开了复杂思维过程的程式化的操作步骤．数学运算不能当作是程式化的操作，数学运算需要理解，数学运算明算理，识算律乃是第一位的．从学习策略的高度审视解题，从解题策略的角度研究运算，学生运算能力不仅会得到提高，学生的数学能力和数学素养也会得到发展．