勤提炼 活运用 促提高——“双A”字基本图形在解题中的应用

☉湖北省阳新县白沙中学 罗 峻

☉湖北省阳新县白沙中心校 马先明

相似是初中几何的核心模块，是中考中的重要考点，也是考查学生分析问题和解决问题及综合能力的重要载体．相似往往与三角形、四边形、圆等几何图形结合，使问题的难度加大．要突破这一难点，不仅要牢固掌握三角形相似的基本判定、性质和相关定理，还需要借助丰富的图形识别经验．为此在平时教学中，我们要适当提炼一些基本图形，并有意识地进行基本图形专题方面的训练，进行几何基本图形的识别和运用．下面结合近年的中考、竞赛试题，提炼出相似问题中常见的“双A”字图形，让我们体会基本图形在解题中化隐为显、化难为易的作用．

一、“双A”字图形及其基本结论

图1

从上面基本图形（图1）的结构看，像两个并排着的背靠背的英文字母“A”，我们暂且称之为“双A”字图形.若熟悉上面基本图形的结构特点，在平时学习中，对于几何图形比较复杂的试题，便能较快地分离出隐藏于其中的基本图形，抓住问题的本质，从而快速解决问题.

二、直接运用基本图形解题

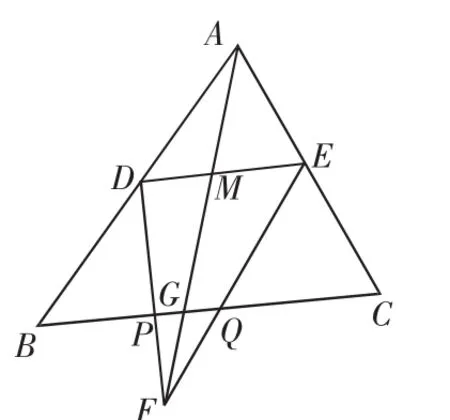
图2

解析：所证的四条线段都在同一条直线上，无法直接运用相似的性质证明，可尝试寻求过渡比实现解题．找出这四条线段所在的三角形，很快发现DM、ME与所证结论有关联，且这六条线段存在于两个“双A”字图形中，其中一个“双A”字图形是倒放着的．

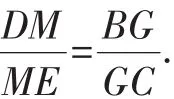
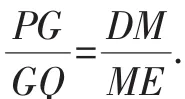
点评：根据所证结论并结合题设图形的鲜明特征，找出其中隐藏着的“双A”字图形，运用该图形的结论，得出比例式，利用过渡比便可快速证题.

例2（济宁中考题）在一次数学课上，一位同学提出：“谁能帮我用一副没有刻度的三角板找出线段AB的中点？”小华说：“我能做到，我的做法是，用这副三角板任作一条直线MN∥AB；在直线AB、MN的同侧任取一点P，连接PA、PB，分别交直线MN于C、D；再连接AD、BC，相交于点E；画射线PE交线段AB于点O，点O就是线段AB的中点.”你认为O是线段AB的中点吗？说明理由.

解析：先按照题意画出如图3所示的图形.

因为CD∥AB，结合“双A”字图形和结论（1），知：

图3

点评：由两条直线平行的条件可看出题设图形中隐藏着的“双A”字图形，同时还隐藏着“8”字型的对顶三角形，这样得出相关的比例线段，用过渡比实现证题．

例3 （武汉中考题）在△ABC中，∠BAC=90°，正方形DEFG的四个顶点在△ABC的边上，连接AG、AF，分别交DE于M、N两点.

（1）如图4，若AB=AC=1，直接写出MN的长；

图4

（2）如图5，求证：MN2=DM·EN.

图5

又GF=DG=EF，即GF2=CF·BG.①

由DE∥BC，利用“双A字”图形及结论（1），知：

结合①和②，得MN2=DM·EN.

点评：本题是相似与三角形、四边形相结合的综合题，要运用相似的性质进行解题，而解题的关键在于运用基本图形快速得出相关线段成比例.其中，第一问是“双A”字基本图形的直接应用；第二问除了“双A”字图形外，还蕴含有“两角对应相等的三角形相似”的基本图形，由相似的性质得出比例式，两者有机结合，使问题易于解决.

从几何图形中直接分离出基本图形，运用图形的性质相对容易，而如何从几何图形中构造出基本图形进行运用，是解题的难点所在.为此必须仔细观察题目给予的图形并研究图形的结构特点，结合已知条件或所求、所证内容，产生丰富联想，构造出能解决问题的基本图形.

三、构造基本图形解题

图6

图7

解析：（1）图6中，由AB为直径，AP为切线，易知AF⊥AB.又CD⊥AB，则CD∥AF.

在“8字”型的对顶三角形中，△ECF≌△EOB（SAS），因此∠FCE=∠EOB=90°，则直线CF是半圆O的切线.

（2）连接BC并延长交AP于点G，连接AC、CO（如图7）.

由第一问的CD∥AF，CE=DE，利用“双A”字图形的结论（3），知FG=FA.

在Rt△ACG中，FC为斜边AG的中线，因此FC=FA，则∠FCA=∠FAC.

又∠OCA=∠OAC，则∠FCO=∠FCA+∠OCA=∠FAC+∠OAC=∠FAO=90°，故FC是半圆O的切线.

点评：本题是一道探索性问题，第一问通过问题的特殊情形探究图形的本质属性，第二问从特殊化向一般情形拓广，进一步探索结论的“不变性”．虽然能猜测结论不变，但求证它较难．此处由“CD∥AF”和“E为CD的中点”这两个条件，联想到构造出“双A”字图形，运用基本图形的结论得出点F为AG的中点，再运用圆、直角三角形、等腰三角形的有关性质进行综合运用．

例5 如图8，在△ABC中，∠BAC=90°，AD⊥BC于D，P是AD的中点，BP的延长线交AC于E，EF⊥BC于F.求证：EF2=AE·EC．

解析：由已知条件AD⊥BC、EF⊥BC，知AD∥EF，延长FE交BA的延长线于点G，就可以构造出“双A”字图形．

由AD∥EF和AP=DP，利用结论（3），知EG=EF.

图8

点评：根据条件“P是AD的中点”和AD∥EF，将图形补全，便构造出“双A”字图形，再运用其性质可快速解题．可见，熟悉基本图形的特征，是正确作出辅助线的前提．

例6（2003年全国数学竞赛）如图9，已知AB是⊙O的直径，BC是⊙O的切线，OC平行于弦AD，过点D作DE⊥AB，垂足为E，连接AC，与DE交于点P，问：EP与PD是否相等？证明你的结论．

解析：由已知条件“AB是⊙O的直径，BC是⊙O的切线”，易知：BC⊥AB.又DE⊥AB，所以DE∥BC．根据已有结果DE∥BC，以及图形的结构特点，还有猜想的结论EP=PD，易联想到“双A”字基本图形，由此延长AD、BC交于点F．

图9

说明：本题是一道结论开放性问题，需用到两个基本图形：“双A”字基本图形和“单A”字基本图形进行解题，难点在于作出合适的辅助线，这需要根据已知条件和所证结论逆向思考，产生联想，让看似并不存在的基本图形显露出来，产生作用．

四、综合运用基本图形解题

例7 如图10，在△ABC中，BD=DC，O是AD上一点，BO、CO的延长线分别交AC、AB于F、E.求证：AD平分EF．

图10

简解：设AD与EF交于点G，过点A作BC的平行线，与CE、BF的延长线分别交于M、N．

点评：由已知条件和所证结论，猜测可能要用到本文中的基本图形，但缺少平行线这个条件，故突破问题的关键在于证EF∥BC，为此过点A作BC的平行线，再运用相似的性质综合解题．本题难度大，原因有三：一是构造“8”字型基本图形；二是利用“双A”字基本图形的性质解题；三是图10中出现多个基本图形的叠加和隐藏.

在“双A”字基本图形中，由EF∥BC，BD=CD，运用结论（3），得EG=FG，即AD平分EF．

图11

简证：过点C作AB的平行线，交PA、PB的延长线于点F、G．

PA为⊙O的切线，由弦切角定理，知∠FAC＝∠ABC.

由AB∥CG，得∠BCG＝∠ABC.

因此∠FAC＝∠BCG.①

由切线长定理，知PA＝PB.又AB∥FG，则△PFG为等腰三角形，所以∠F＝∠G.②

点评：此题是一道颇有难度的竞赛题，原解法运用相似三角形得出多个比例式，再将它们乘除运算，曲折迂回，不易思考．这里结合题设的图形，构造出“双A”字基本图形，并利用结论（1）、相似三角形的性质和面积比进行证明，直观明了，简捷易懂．

例9（全国初中联赛）如图12，设凸四边形ABCD的对角线AC与BD交于点M，过点M作AD的平行线分别与AB、CD交于点E、F，与BC的延长线交于点O，P是以O为圆心、OM为半径的圆上一点.求证：∠OPF=∠OEP.

图12

图13

证明：如图13，延长BC、AD交于点H.

又∠FOP=∠POE，利用“两边对应成比例且夹角相等的两三角形相似”，得△OFP∽△OPE，因此对应角∠OPF=∠OEP．

五、教学反思

数学是关于数与形的科学，形是数学的重要表现形式，学习数学离不开对几何图形的研究．《数学课程标准》在几何方面的学习要求是“能从较复杂的图形中分解出基本的图形，并能分析其中的基本元素及其关系，利用直观来进行思考”．可见从复杂图形中“离析”出基本图形，是解决图形问题必须具备的重要能力之一，也是解决几何问题的重要方法．同时数学也是关于模式的科学，这反映在数学解题时，需要进行模式识别，需要构建标准的模型．当我们面对一个陌生的、看似复杂的几何问题时，往往都可以将它转化为已解决过的、较熟悉的、简单的几何图形，这里用到的基本图形就是解决问题的一个模式．用基本图形来分析、解决问题，是解题的常用方法、通用方法，可以发挥数学教学的长期效益．因此，必须重视基本图形在解题中的作用．

总体来说，数学中的基本图形分为两种：一种是教材中的定义、定理和性质所对应的图形——单一型基本图形，这些图形一般都有与概念或定理的条件及结论的外形相呼应的结构特征，像直线、平行线、相交线、三角形、四边形、点与圆、圆的切线、弦切角等都属于单一型基本图形；另一种基本图形是例题和习题所对应的图形——复合型基本图形，它是单一型基本图形内容的扩展与延伸，它常常把一些重要的、常用图形加入到单一型基本图形成为复合型基本图形的一部分，一般而言复合型基本图形都由两个或两个以上的单一型基本图形组合而成，所蕴含的结论更丰富、实用性也比较强．比如：角平分线和平行线组合成为等腰三角形，一线三垂直（即在同一直线上，有三个直角）图形可产生三角形全等或相似，圆的切线长基本图形中蕴含有多对三角形全等、多对线段相等、多对角相等……复合型基本图形在课本中以例题、习题的形式零散出现，我们应引导学生收集与归纳．

学生对于单一型基本图形一般较熟悉，用的比较得心应手；而对于复合型基本图形，虽然知道图形与结论，但在解题时却常常忽略它的存在，导致解题困难或失败.为什么单独把这些复合型基本图形提出来，学生马上就知道其结论，而解题时却熟视无睹？这就要求我们在教学过程中，一方面应重视基础知识、基本技能、基本方法的教学，注重对知识的发生、发展过程的揭示，因为定理、公式推证的过程就蕴含着重要的解题方法和规律，教师应该充分暴露思维过程，发掘其内在的规律.长此以往，学生便可以潜移默化，学会解决问题的思考方法.另一方面，注重对这些基本图形的提炼并会灵活运用.要引导学生研究这些看似不起眼的复合型基本图形，分析基本图形的特征，归纳基本图形的性质，深刻掌握基本图形，理解基本图形的性质都是以怎样的方式发挥作用.

为此，在平时的教学中，应该培养学生对一些基本题型和基本图形的敏锐观察力，借给学生一双“数学慧眼”.在每学习一部分课本内容后，可以尝试以“专题讲座”的教学模式，引导学生自主探索、自我总结、逐步提高，对课本的这部分例题、习题加以提炼并深刻研究，形成结论储备起来，达到“见到图形，想到性质；想到性质，想全图形”的要求，在头脑中形成系统完备的待用基本图形库，最终把基本图形当作利刃，用到解题中去.

总之，引导学生提炼总结课本中的基本图形，并运用基本图形解题，不仅有助于激发学生的学习兴趣，提高解题效率，而且对发展学生的数学思维能力，培养学生的创新意识具有重要的现实意义.