例析“动点的路径长”中考压轴题解题策略
☉江苏省淮安市淮海中学 张建华
著名数学家弗兰登塔尔曾说:“从来没有一种数学的思想会像当初被发现时那样付诸文字,一旦问题解决了,思考的程序便颠倒过来,把火热的思考变成冰冷的美丽”.动点问题是近年来中考的热点,其中有关直接写出动点的路径长的中考题也备受各地中考命题者的青睐,由于动点所经过的路径是隐性的,这类试题能全面考查数学活动过程、数学活动经验的积累、解决问题的能力及数学应用意识和创新意识,动点问题要经过火热的思考,才能得出冰冷的美丽,因此,这类问题常是填空题、选择题、解答题中的压轴题,而在解答题中常是直接写出动点的路径长.
一、解题策略
因动点所经过的路径长可求,故常见的动点所经过的路径有线段和圆弧两类.路径虽是“隐性”,但用三点这“X光”显其形(即起点、过程点和终点三点确定其形状),五步解决问题.具体五步是:一画,画出动点的起点、过程点和终点;二看,观察三点是否在一直线上;三猜想,在一直线上是线段,不在一直线上是圆弧;四验证,线段型常用中位线或垂直平分线等知识解决,圆弧型常利用“有对称性”和“90°的圆周角所对弦是直径”等知识确定圆心和半径;五计算,常用勾股定理、相似三角形等知识进行求解.多媒体的普及,对于数学教学的作用是不容忽视的,特别是几何画板在解决动态问题的作用真是妙不可言的,让我们在图形变化的过程中体验、把握、认知数学的美.本文例举近几年的中考题进行归类剖析,供2013年中考复习教学参考,并试图用几何画板进行动感体验.
二、分类剖解

图1
(一)线段型
1.中位线型
例1 (2012年湖南张家界)如图1,已知线段AB=6,C、D是AB上两点,且AC=DB=1,P是线段CD上一动点,在AB同侧分别作等边三角形APE和等边三角形PBF,G为线段EF的中点,点P由点C移动到点D时,G点移动的路径长度为______.
解析:如图1,分别延长AE、BF交于点H,连接HD,过点G作MN∥AB分别交HA、HD于点M、N.
因为△APE和△PBF是等边三角形,所以∠A=∠FPB=60°,∠B=∠EPA=60°.
所以AH∥PF,BH∥PE.
所以四边形EPFH为平行四边形.
所以EF与HP互相平分.
因为点G为EF的中点,所以点G也正好为PH中点,即在点P的运动过程中,点G始终为PH的中点.
所以点G的运行轨迹为△HCD的中位线MN.
因为AB=6,AC=DB=1,所以CD=6-1-1=4.
所以MN=2,即G的移动路径长为2.
动感体验:打开几何画板:(1)[绘图]→[定义坐标系]→在x轴上取点A、C、D、B→选中点C、D→[构造]→[线段]→在线段CD上取点P→选中线段CD→右键→[隐藏线段];(2)选中点A、P→[构造]→[线段]→双击点A→[变换]→[旋转]→[固定角60度]→回车得到线段AE→点A、E→[构造]→[线段]→等边△APE;(3)同样方法构造等边△BPF;(4)点E、F→[构造]→[线段]→选中EF→[构造]→[中点]→记为G.
如图2,选中点G,右键→[追踪点],拖动点P,G点的路径是一线段.
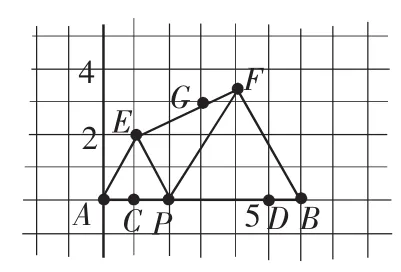
图2
例2(2010年江苏南京)如图3,正方形ABCD的边长是2,M是AD的中点,点E从点A出发,沿AB运动到点B停止,连接EM并延长交射线CD于点F,过M作EF的垂线交射线BC于点G,连接EG、FG.
(1)设AE=x时,△EGF的面积为y,求y关于x的函数关系式,并写出自变量x的取值范围;
(2)P是MG的中点,请直接写出点P的运动路线的长.

图3

图4
分析:(1)略.(2)如图4,画出当动点E在起点E1、过程中E1E2上、终点E2时,对应P点为P1、P和P2,发现P1、P、P2这三点在一直线上,易证点P的路径为△MG1G2的中位线,又易证△MG1G2∽△BAM,从而求出G1G2=4,故P1P2=2.

当点E与点A不重合时,0<x≤2.
在正方形ABCD中,∠A=∠ADC=90°,
所以∠MDF=90°,所以∠A=∠MDF.
因为AM=DM,∠AME=∠DMF,所以△AME≌△DMF.所以ME=MF.

过M作MN⊥BC于N,则∠MNG=90°,∠AMN=90°.
因为MN=AB=AD=2AM,所以∠AME+∠EMN=90°.
因为∠EMG=90°,所以∠NMG+∠EMN=90°.
所以∠AME=∠GMN,所以Rt△AME∽Rt△NMG.

所以y=2x2+2(0≤x≤2).
(2)点P的运动路线长为2.
动感体验:打开几何画板:(1)[绘图]→[定义坐标系]→在y轴上取点A,原点B→选中点A、B→[构造]→[线段]→双击点A→[变换]→[旋转]→[固定角90°]→回车得到线段选中线段AD,同样方法将线段AD绕点D旋转90°,得线段CD,连接BC,得正方形ABCD;(2)选中线段AD→[构造]→[中点]得AD中点M;(3)在线段AB上取一点E→选中E、M→[构造]→[射线];(4)选中线段CD→右键→[隐藏线段]→选中C、D→[构造]→[射线],两射线交点为F;(5)选中M、射线EM→[构造]→[垂线]→交BC于点G;(6)选中射线ME→右键→[隐藏射线]→选中点M、G→[构造]→[线段]→[构造]→[中点]记为P.

图5
如图5,选中点P,右键→[追踪点].拖动点E,P点的路径是一线段.
2.线段的垂直平分线型
例3(2011年福建三明)在矩形ABCD中,点P在AD上,AB=2,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB,BC于点E,F,连接EF(如图6).

图6

图7
(1)当点E与点B重合时,点F恰好与点C重合(如图7),求PC的长.
(2)探究:将直尺从图7中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中,请你观察、猜想,并解答:
①tan∠PEF的值是否发生变化?请说明理由.
②直接写出从开始到停止,线段EF的中点经过的路线长.

图8

图9


又因为∠BPC=90°,所以∠APB+∠DPC=90°.
所以∠ABP=∠DPC.


(2)①tan∠PEF的值不变.
理由:过点F作FG⊥AD,垂足为点G,则四边形ABFG是矩形.
所以∠A=∠PFG=90°,GF=AB=2.
所以∠AEP+∠APE=90°.
又因为∠EPF=90°,所以∠APE+∠GPF=90°.
所以∠AEP=∠GPF,所以△APE∽△GPF.

所以tan∠PEF的值不变.

(二)圆弧型
1.利用对称性确定圆心和半径
例4 (2012年江苏镇江)在平面直角坐标系xOy中,点A的坐标为(0,2),直线OP经过原点,且位于第一、三象限,∠AOP=45°(如图10),设点A关于直线OP的对称点为B.
(1)写出点B的坐标______.
(2)过原点O的直线l从直线OP的位置开始,绕原点O顺时针旋转.
①当直线l沿顺时针方向旋转10°到直线l1的位置时(如图10),点A关于直线l1的对称点为C,则∠BOC的度数是______,线段OC的长为______;
②当直线l沿顺时针方向旋转55°到直线l2的位置时(如图11),点A关于直线l2的对称点为D,则∠BOD的度数是______;
③当直线l沿顺时针方向旋转n°(0<n≤90°)时,在这个运动过程中,点A关于直线l的对称点所经过的路径长为______(用含n的代数式表示).

图10

图11
解析:(1)如图10,由∠AOP=45°,点A在y轴上,得点A关于直线OP的对称点B在x轴上.根据“轴对称和线段垂直平分线上的点到线段两端距离相等”的性质可知B(2,0).

动感体验:打开几何画板:(1)[绘图]→[定义坐标系]→在y轴上取点A(0,2);(2) 点击画圆工具→画出⊙O;(3)任取点C,选中O、C→[构造]→[直线],得直线l;(4)选中点A、直线l→[构造]→[垂线],交⊙O于点B;(5)选中⊙O→右键→[隐藏圆].

图12
如图12,选中点B,右键→[追踪点].旋转直线l,B点的路径是圆.
2.利用90°的圆周角所对弦是直径确定圆心和半径
例5(2011年浙江湖州)如图13,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.
(1)求点D的坐标(用含m的代数式表示);
(2)当△APD是等腰三角形时,求m的值;
(3)设过P、M、B三点的抛物线与x轴正半轴交于点E,过点O作直线ME的垂线,垂足为H(如图14),当点P从点O向点C运动时,点H也随之运动.请直接写出点H所经过的路径长.(不必写解答过程)

图13

图14

图15

解:(1)由题意得CM=BM.
因为∠PMC=∠DMB,所以Rt△PMC≌Rt△DMB.
所以DB=PC,所以DB=2-m,AD=4-m.
所以点D的坐标为(2,4-m).

②若PD=PA,过P作PF⊥AB于点F(如图13),


③若PD=DA,因为△PMC≌△DMB,





动感体验:打开几何画板:(1)[绘图]→[定义坐标系]中,画出正方形ABCD.(2)选中线段BC→[构造]→[中点]得BC中点M.(3)在OC上取点P→[度量]→[纵坐标],记为m;同样方法,点M的横坐标为xm点B的纵坐标为yB.(4)[数据]→[新建函数]→输入g(x)→回车→选中g(x)右键→[绘制函数],得抛物线g(x).(5)抛物线g(x)与x轴交点为E.(6)选中M、E→[构造]→[直线]→选中O→[构造]→[垂线],垂足为H.
如图16,选中点H,右键→[追踪点].拖动P,H点的路径是圆弧.

图16
三、几点思考
1.要引导学生解题后要反思
在解题过程中,要求学生不能仅满足于问题已解决,要引导学生审视问题,探究问题的本质,通过归纳总结,从而提高学生的思维水平,使思维得到拓展,从而达到做一题会一类,甚至知一片的目的.
2.没有过程就没有思想
在教学中,让学生自主探究问题的过程,要留有余地,让学生有思有想,培养学生解决问题的方法,体会从几个特殊点入手,通过观察、猜想、验证、证明的过程,从中积累经验,从而达到“授之以渔”的目的.
3.要通过典型问题,进行适当拓展
在中考复习时,要立足课本,瞄准课标和中考说明,既要训练好基础题,也要在知识方法上适当拓展,提高学生中考的适应性.
4.不断更新教学理念,提高教学能力
教学中要不断更新教学理念,提高教学能力,多媒体的普及,对于数学教学的作用是不容忽视的,特别是几何画板在解决动态问题的演示时,很直观地让我们在图形变化的过程中体验、把握、认知数学的美.因此,作为教师也要不断地学习,才能与时俱进,为提高教学质量而达到事半功倍的效果.

