基于阴影变换的动态灰值形态算子的研究

段 汕，冯光琼，赵淑珍，谢英华

(中南民族大学 数学与统计学学院， 武汉 430074)

1964 年G.Matheron 和J.Serra 在法国巴黎矿业学院共同创立了数学形态学，它是一门建立在严格数学理论基础之上的学科，其基本思想和方法对图像处理的理论和技术产生了重大影响[1].数学形态学具有完备的数学理论，为形态学方法用于图像分析和处理等各项工程技术领域奠定了坚实的基础，同时这也使得数学形态学中数学理论的研究显得尤为重要[2，3].

最初的数学形态学理论主要集中于固定结构元下的二值形态算子的研究，随后Serra、Heijmans等学者将二值形态算子理论的研究扩展到了灰值图像形态算子理论的研究，如文献[4-6]中作者通过阴影变换和表面算子的理论将函数与集合进行相互转化，实现了数学形态学理论从二值形态学到灰值形态学的扩展.然而随着形态学应用领域的不断发展，基于固定不变的结构元进行图像处理有时达不到理想效果，因此Beucher 、Debayle等很多学者基于空间变化(Spatially-Variant)的思想对自适应的形态学的理论及应用方面进行了研究，如文献[7-9]中作者研究了自适应算子的理论及广泛应用.同时，Bouaynaya、Schonfeld 等学者在文献[10,11]中以固定结构元下的二值形态学理论为基础，研究了动态结构元下的二值形态算子，在文献[12]中以固定结构元下的灰值形态学理论为基础，探讨了动态结构元下的灰值形态算子(即给出了SV灰值形态学的腐蚀、膨胀以及开闭算子的代数形式)，实现了从固定结构元下的形态学理论向SV的形态学理论的扩展.文献[13]则为欧式空间中SV(二值和灰值)的数学形态学理论提供了统一框架，并用阴影变换和表面算子表示了SV灰值形态学的腐蚀和膨胀算子，本文在此基础之上，基于阴影变换和表面算子的理论系统地研究了在SV的二值形态学理论的基础上建立SV灰值形态算子的方法.首先，从阴影集的概念出发，证明了阴影集的相关结论，其次，运用阴影变换和表面算子表示了SV灰值形态学的开闭算子，并以文献[11]中的SV二值形态学理论为基础， 证明了文献[13]中的腐蚀、膨胀以及本文的开这3种算子的表示形式具有文献[12]中所给出的对应算子的代数形式，最后，研究了腐蚀、膨胀以及开闭这4种算子的相关性质，从而实现了从SV的二值形态算子的研究到SV的灰值形态算子的研究的扩展.

1 预备知识

为了方便下文的研究，通过文献[4]和[13]，我们引入相关概念.

考虑非空集合E=Rn或Zn(n>0)，定义SV二值结构元素θ是从E到P(E)的映射，并将θ′(y)={z∈E：y∈θ(z)}(y∈E)称为θ的转置结构元素. 在欧式空间中， SV二值腐蚀、膨胀、开、闭算子分别表示为：

(1)

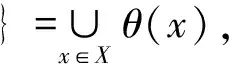
(2)

Γθ(X)=δθ(εθ(X))=∪{θ(y):θ(y)⊆X;

y∈E},

(3)

Φθ(X)=εθ(δθ(X))=∪{z∈E:θ(y)∩X≠∅,

∀θ(y):z∈θ(y)},

(4)

其中X∈P(E).在下文中，我们用大写字母X，Y，Z表示P(E)中的元素，小写字母x，y，z表示E中的元素.

通过阴影变换的方法，我们可实现从SV二值形态算子到SV灰值形态算子的扩展.本文仅考虑从E=Rn或Zn(n>0)到T=R或Z的上半连续函数的集合，记作USC(E,T).A∈Rn×R称为阴影集当且仅当对任意的(x,t)∈A，必有(x,t′)∈A对一切t′≤t成立.对任意的f∈USC(E,T)，将函数f的阴影集定义为U[f]={(x,y)∈E×T:y≤f(x)}.对任意的阴影集V，定义其表面为从E到T的函数S[V]，即S[V](x)=∨{y∈T:(x,y)∈V}.很容易得到，对任意的f∈USC(E,T)，均有S(U[f])=f. SV结构函数Θ定义为从E到USC(E,T)的映射，若对任意的x,u∈E，均有[Θ′(x)](u)=[Θ(u)](x)，则将Θ′称为Θ的转置映射.为了实现函数集合化，我们定义阴影集结构元ΘU：ΘU(x,y)=U[Θ(x)+y]=U[Θ(x)]+y((x,y)∈E×T).本文假定Θ是连续的，且对E中的每一点x，Spt(Θ′(x))都是紧集.

为了进行下文的研究，我们首先给出以下几个引理.

引理1 对任意的f1，f2∈USC(E,T) ，均有f1≤f2⟺U[f1]⊆U[f2]成立.

证明必要性.若f1≤f2，即对任意的x∈E，都有f1(x)≤f2(x)，则对任意的(x,y)∈U[f1]，有y≤f1(x)≤f2(x)，从而可得(x,y)∈U[f2]. 因此U[f1]⊆U[f2].

充分性.若U[f1]⊆U[f2]，即{(x,y)|y≤f1(x)}⊆{(x,y)|y≤f2(x)}，则对任意(x,y)∈E×T，有y≤f1(x)⟹y≤f2(x).从而有∨{y|y≤f1(x)}≤∨{y|y≤f2(x)}，也即∨{y|(x,y)∈U[f1]}≤∨{y|(x,y)≤U[f2]}.又由表面函数的定义，可知对任意的x∈E， 都有S(U[f1])(x)≤S(U[f2])(x)，即f1(x)≤f2(x).

引理2 若A∈Rn×R是阴影集，则有U(S(A))=A成立.

证明一方面，由于(S(A))(x)=∨{y|(x,y)∈A}， 则对任意的(x,y)∈A，有y≤(S(A))(x)，又因为U(S(A))={(x,y)|y≤(S(A))(x)}，于是有(x,y)∈U(S(A)). 从而可得A⊆U(S(A)).另一方面， 对任意的(x,y)∈U(S(A))，都有y≤(S(A))(x)=∨{y′|(x,y′)∈A}，则对任意的y′≥y，均有(x,y′)∈A.故由阴影集的定义可知，(x,y)∈A.也即U(S(A))⊆A.综上所述，可得U(S(A))=A成立.

引理3 对任意的f∈USC(E,T)，εΘU(U[f])和δΘU(U[f])均是阴影集.

证明1) 由(1)式可知，我们有εΘU(U[f])={(x,y)|ΘU(x,y)⊆U[f]}，则对任意的(x,y)∈εΘU(U[f])，有ΘU(x,y)⊆U[f]，也即U[Θ(x)+y]⊆U[f]，根据引理1可得，Θ(x)+y≤f.则对任意的y′≤y，有Θ(x)+y′≤Θ(x)+y≤f，于是有U[Θ(x)+y′]⊆U[f]，即ΘU(x,y′)⊆U[f]，从而可得(x,y′)∈εΘU(U[f]).故由阴影集的定义知εΘU(U[f])是阴影集.

由于对任意的f∈USC(E,T)， 有ΓΘU(U[f])=δΘU(εΘU(U[f]))，ΦΘU(U[f])=εΘU(δΘU(U[f])).由引理3知，ΓΘU(U[f])和ΦΘU(U[f])也都是阴影集.

根据引理2及引理3，容易得到性质1.

性质1 对任意的f∈USC(E,T)，以下4个等式成立:

U(S(εΘU(U[f])))=εΘU(U[f]),U(S(δΘU(U[f])))=δΘU(U[f]),U(S(ΓΘU(U[f])))=ΓΘU(U[f]),U(S(ΦΘU(U[f])))=ΦΘU(U[f]).

2 SV灰值形态算子的表示形式的研究

为了将SV的二值形态算子扩展到SV的灰值形态算子，阴影变换便成了重要的方法与途径.N .Bouaynaya和 D .Schonfeld在SV二值形态学的腐蚀和膨胀算子的表示形式的基础之上，运用阴影变换和表面算子表示了SV灰值形态学的腐蚀和膨胀算子，具体形式如下[13]：

[εΘ(f)](x)=S[εΘU(U[f])](x)

(∀x∈E,f∈USC(E,T))，

(5)

[δΘ(f)](x)=S[δΘU(U[f])](x)

(∀x∈E,f∈USC(E,T)).

(6)

我们按照二值形态学开闭算子的定义方式(即腐蚀和膨胀的复合)，利用阴影变换和表面算子得到SV灰值形态学的开闭算子的表示形式.

性质2 SV灰值形态学的开和闭算子可以分别表示为:

[ΓΘ(f)](x)=δΘ(εΘ(f))(x)=

S[ΓΘU(U[f])](x)(∀x∈E,f∈USC(E,T)).

[ΦΘ(f)](x)=εΘ(δΘ(f))(x)=

S[ΦΘU(U[f])](x)(∀x∈E,f∈USC(E,T)).

证明1)由(5)、(6)式，可得对任意的x∈E，有:

[ΓΘ(f)](x)=δΘ(εΘ(f))(x)=

S(δΘU(U(S(εΘU(U[f])))))(x).

又由性质1，有:

[ΓΘ(f)](x)=S(δΘU(εΘU(U[f])))(x)=

S(ΓΘU(U[f]))(x).

2) 由(5)、(6)式，可得对任意的x∈E，都有:

[ΦΘ(f)](x)=εΘ(δΘ(f))(x)=

S(εΘU(U(S(δΘU(U[f])))))(x).

又由性质1，有:

[ΦΘ(f)](x)=S(εΘU(δΘU(U[f])))(x)=

S(ΦΘU(U[f]))(x).

以SV的二值形态学理论为基础，通过阴影变换和表面算子的理论建立了SV灰值形态算子的表示形式.根据SV灰值形态腐蚀、膨胀以及开算子的表示形式，我们可以推证这3种算子具有其对应的代数形式.

证明由(5)式和表面函数的定义，可得对任意的x∈E，均有[εΘ(f)](x)=∨{v∈T:(x,v)∈εΘU(U[f])}.又由(1)式和ΘU(x,y)=U[Θ(x)+y]，从而可得:

[εΘ(f)](x)=∨{v∈T:ΘU(u,v)⊆U[f]}=

∨{v∈T:U[Θ(x)+v]⊆U[f]} .

由引理1可知，[εΘ(f)](x)=∨{v∈T:Θ(x)+v≤f}=∨{v∈T:v≤f-Θ(x)} .

性质4 SV灰值形态学膨胀也可表示为：∀x∈E，∀f∈USC(E,T)，[δΘ(f)](x)=

证明由(6)式和表面函数的定义，可得对任意的x∈E，都有[δΘ(f)](x)=∨{v∈T:(x,v)∈δΘU(U[f])} .又由(2)式，可得对任意的f∈USC(E,T)，均有δΘU(U[f])={(x,v)∈E×T:(ΘU)′(x,v)∩U[f]≠∅}.从而可得，[δΘ(f)](x)=∨{v∈T:(x,v)∈E×T,(ΘU)′(x,v)∩U[f]≠∅}.

也即[δΘ(f)](x)=∨{v∈T:(x,v)∈E×T,∃(u,w)∈(ΘU)′(x,v)∩U[f]}.

又因为(ΘU)′(x,v)={(u,w)∈E×T:(x,v)∈ΘU(u,w)}，于是有：

[δΘ(f)](x)=∨{v∈T:(x,v)∈E×T,∃(u,w),(x,v)∈ΘU(u,w)且(u,w)∈U[f]}=∨{v∈T:(x,v)∈E×T,∃(u,w),v≤[Θ(u)](x)+w且w≤f(u)}.

又[Θ′(x)](u)=[Θ(u)](x)，因此有：

[δΘ(f)](x)=∨{v∈T:(x,v)∈E×T,∃(u,w),v≤[Θ′(x)](u)+w且w≤f(u)}=∨{v∈T:(x,v)∈E×T,∃(u,w),v≤[Θ′(x)](u)+f(u)}.

[Θ′(x)](u)}.

根据上确界的定义，有[δΘ(f)](x)=∧{v:v≥f(u)+[Θ′(x)](u)}.即：

[δΘ(f)](x)=∧{v:-Θ′(x)+v≥f}.

性质5 SV灰值形态学开也可表示为：∀f∈USC(E,T) ，∀x∈E，

[ΓΘ(f)](x)=∨{Θ(u)+v≤f:(u,v)∈E×T}.

证明由性质2和表面函数的定义，可得对任意的x∈E，均有[ΓΘ(f)](x)=∨{b|(a,b)∈ΓΘU(U[f])}.又由(3)式，可得对任意的f∈USC(E,T)，都有[ΓΘ(f)](x)=∨{b|(a,b)∈∪{ΘU(x,y):ΘU(x,y)⊆U[f];(x,y)∈E×T},(a,b)∈E×T}.也即[ΓΘ(f)](x)=∨{b|∃(u,v)∈E×T,(a,b)∈ΘU(u,v)且ΘU(u,v)⊆U[f]}.又由于ΘU(x,y)=U[Θ(x)+y]和引理1，从而可得[ΓΘ(f)](x)=∨{b|b≤[Θ(u)](a)+v且Θ(u)+v≤f}.即[ΓΘ(f)](x)=∨{Θ(u)+v≤f,(u,v)∈E×T}.

3 SV灰值形态算子的性质

以上的研究利用阴影变换和表面算子，在SV二值形态算子的表示形式的基础上建立了SV灰值形态算子.SV灰值形态学腐蚀、膨胀以及开闭算子具有与SV二值形态学腐蚀、膨胀以及开闭算子相似的性质.下面我们将以SV二值形态算子的性质为基础来证明SV灰值形态算子的对应性质.

3.1 腐蚀和膨胀的性质

性质6(附益性) 对任意的结构函数映射Θ，δΘ(f)≤g⟺f≤εΘ(g)(f,g∈USC(E,T)).

证明由(6)式和δΘ(f)≤g可得S(δΘU(U[f]))≤g.根据引理1，我们有U(S(δΘU(U[f])))⊆U[g].从而由性质1可知δΘU(U[f])⊆U[g].故由SV二值形态学腐蚀和膨胀的附益性可得U[f]⊆εΘU(U[g]).又由表面函数的定义，可得S(U[f])≤S(εΘU(U[g])).即f≤εΘ(g) .

该性质表明SV的灰值腐蚀与膨胀具有附益性.

性质7(增性) 若f1，f2∈USC(E,T)，f1≤f2，那么对任意的结构函数映射Θ，有εΘ(f1)≤εΘ(f2)，δΘ(f1)≤δΘ(f2).

证明若f1，f2∈USC(E,T)且f1≤f2，则根据引理1和SV二值腐蚀和膨胀的增性， 有εΘU(U[f1])⊆εΘU(U[f2])，δΘU(U[f1])⊆δΘU(U[f2]).又由表面函数的定义，我们可得对任意的x∈E，均有S(εΘU(U[f1]))(x)≤S(εΘU(U[f2]))(x)，S(δΘU(U[f1]))(x)≤S(δΘU(U[f2]))(x).由(5)和(6)式 ，可得εΘ(f1)≤εΘ(f2),δΘ(f1)≤δΘ(f2).

此性质说明对于目标信号，SV灰值腐蚀和膨胀都满足递增性.

性质8 (扩展性、非扩展性) 如果对任意的x∈E，[Θ(x)](x)≥0，那么εΘ(f)≤f，δΘ(f)≥f(f∈USC(E,T)).

证明由于对任意的x∈E，[Θ(x)](x)≥0，则对任意的(x,y)∈Ε×T，都有[Θ(x)+y](x)≥y.也即(x,y)∈U[Θ(x)+y]=ΘU(x,y).故根据SV二值腐蚀的非扩展性和膨胀的扩展性，知对任意的f∈USC(E,T)，我们有εΘU(U[f])⊆U[f]，U[f]⊆δΘU(U[f]).又由(5)、(6)式，得εΘ(f)(x)=S(εΘU(U[f]))(x)≤S(U[f])(x)=f(x)，δΘ(f)(x)=S(δΘU(U[f]))(x)≥S(U[f])(x)=f(x).从而有εΘ(f)≤f，δΘ(f)≥f.

由此性质可见SV灰值腐蚀是非扩展的，而膨胀是扩展的.

性质9 (结构元素的增性) 如果结构函数映射Θ1≤Θ2，那么有εΘ2(f)≤εΘ1(f)，δΘ1(f)≤δΘ2(f)(f∈USC(E,T)).

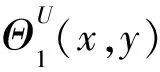
这个性质表明对于结构元素， SV灰值腐蚀与膨胀也满足增性.

为了说明SV灰值腐蚀和膨胀满足结合律，我们首先给出以下两个引理.

引理4 若θ1，θ2是E到P(E)上的映射， 那么δθ2(δθ1)=δδθ2(θ1)，其中δθ1(θ2) 表示E到P(E)上的映射，对任意的z∈E满足(δθ1(θ2))(z)=δθ1(θ2(z)).

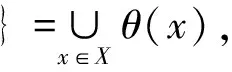
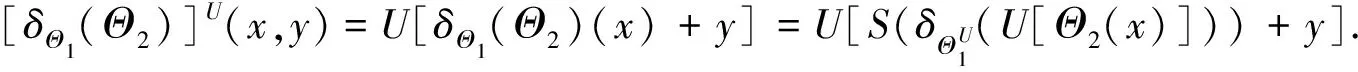
性质10 (结构元素的复合性) 若Θ1、Θ2是从E到USC(E,T)的映射， 那么εΘ2(εΘ1(f))=εδΘ1(Θ2)(f),δΘ2(δΘ1(f))=δδΘ2(Θ1)(f),f∈USC(E,T)， 其中εΘ1(Θ2)和δΘ1(Θ2)均表示从E到USC(E,T)上的映射， 对任意的x∈E满足εΘ1(Θ2)(x)=εΘ1(Θ2(x))，δΘ1(Θ2)(x)=δΘ1(Θ2(x)).

证明(1) 根据SV灰值腐蚀的定义，可得对任意的x∈E，有:

εΘ2(εΘ1(f))(x)=

(2) 根据SV灰值膨胀的定义，我们可得到对任意的x∈E，有:

δΘ2(δΘ1(f))(x)=

δΘ2(δΘ1(f))(x)=

S(δ[δΘ2(Θ1)]U(U[f]))(x)=δδΘ2(Θ1)(f).

3.2 开和闭的性质

性质11(等幂性) 对任意的结构函数映射Θ，

ΦΘ(f)(f∈USC(E,T)).

证明由性质2和性质1，我们可得：

S(ΓΘU(U(S(ΓΘU(U[f])))))=

S(ΓΘU(ΓΘU(U[f]))),

S(ΦΘU(U(S(ΦΘU(U[f])))))=

这个性质说明SV灰值开、闭运算满足幂等性.用同一个结构元素对输入信号作两次(或者两次以上)的开运算(或闭运算)得到的结果和用此结构元素作用一次的结果相同.

性质12(扩展性、非扩展性) 对任意的结构函数映射Θ，ΓΘ(f)≤f，ΦΘ(f)≥f(f∈USC(E,T)).

证明由SV二值形态学开闭算子的扩展与非扩展性，可得对任意的f∈USC(E,T)，有ΓΘU(U[f])⊆U[f]，ΦΘU(U[f])⊇U[f].又由表面函数的定义，我们可得对任意的x∈E，均有

S(ΓΘU(U[f]))(x)≤S(U[f])(x),

S(ΦΘU(U[f]))(x)≥S(U[f])(x).

也即ΓΘ(f)≤f,ΦΘ(f)≥f.

此性质表明SV灰值开是非扩展的，而闭是扩展的.

性质13 (增性) 若f1，f2∈USC(E,T)且f1≤f2，那么对任意的结构函数映射Θ，都有ΓΘ(f1)≤ΓΘ(f2),ΦΘ(f1)≤ΦΘ(f2).

证明若f1,f2∈USC(E,T)且f1≤f2，则由引理1和SV二值开闭算子的增性， 可得ΓΘU(U[f1])⊆ΓΘU(U[f2]),ΦΘU(U[f1])⊆ΦΘU(U[f2])，故由表面函数的定义，我们可得对任意的x∈E，均有S(ΓΘU(U[f1]))(x)≤S(ΓΘU(U[f2]))(x),S(ΦΘU(U[f1]))(x)≤S(ΦΘU(U[f2]))(x)，从而可得ΓΘ(f1)≤ΓΘ(f2)，ΦΘ(f1)≤ΦΘ(f2).

此性质表明对于目标信号，SV灰值开和闭也都满足递增性.

由上述证明可以看出，基于阴影变换和表面算子的理论所给出的SV灰值形态腐蚀、膨胀以及开闭算子，与基于固定结构元下的灰值形态学理论而定义的这4种对应算子的性质基本保持一致.

4 结束语

本文在文献[13]所表示的SV灰值形态学腐蚀、膨胀算子的基础之上，利用阴影变换和表面算子表示了SV灰值形态学的开闭算子，并根据文献[11]中的SV二值形态学理论，证明得到腐蚀、膨胀和开这3种算子的表现形式具有文献[12]中所给出的对应算子定义形式，并进一步探讨了腐蚀、膨胀以及开闭这4种算子的相关性质.通过以上研究，我们可以清晰地看到，SV灰值形态学腐蚀、膨胀以及开闭算子可以基于固定结构元下的灰值形态学理论直接定义而得，也可以运用阴影变换和表面算子来进行建立，这两种途径得到的SV灰值形态算子的表示形式和相关性质基本达成一致，但闭算子的表现形式与其代数形式的一致性以及腐蚀膨胀的对偶性、开闭的对偶性的证明还有待进一步研究.本工作实现了从SV的二值形态算子的研究到SV的灰值形态算子研究的扩展，有助于我们深入地理解SV形态算子，以及整个数学形态学的基本理论，也为今后的腐蚀膨胀的对偶性、开闭的对偶性的研究奠定了基础.

参 考 文 献

[1] 崔 屹. 图像处理与分析——数学形态学方法及应用[M]. 北京：科学出版社，2000.

[2] Serra J. Image analysis and mathematical morphology[M].New York: Academic Press，1982.

[3] Serra J. Image analysis and mathematical morphology II: theoretical advances[M]. New York: Academic Press, 1988.

[4] 龚 炜，石青云，程民德. 数字空间中的数学形态学——理论及应用[M].北京：科学出版社，1997.

[5] Heijmans H. A note on the umbra transform in gray-level morphology[J].Pattern Recognition Letters，1993，14:877-881.

[6] Heijmans H. Morphological image operator[M]. Boston: Academic Press，1994.

[7] Verly J G，Delanoy R L .Adaptive mathematical morphology for range imagery[J].IEEE Transactions on Image Processing, 1993, 2(2):272-275.

[8] Debayle J, Pinoli J. General adaptive neighborhood image processing-part I: introduction and theoretical aspects[J]. Mathematical Imaging and Vision, 2006, 25(2):245-266.

[9] Debayle J, Pinoli J. Multiscale image filtering and segmentation by means of adaptive neighborhood mathematical morphology[C]// IEEE. IEEE International Conference on Image Processing, Genoa:IEEE, 2005(9): 537-540.

[10] Charif-Chefchaouni M, Schonfeld D. Spatially-variant mathematical morphology[C]// IEEE. IEEE International Conference on Image Processing. Chicago:IEEE, 1996(5): 49-56.

[11] Bouaynaya N，Charif-Chefchaouni M，Schonfeld D.Theoretical foundations of spatially-variant mathe-matical morphology part I: binary images[J].IEEE Trans on Pattern Analysis and Machine Intelligence, 2008, 30(5):823-836.

[12] Bouaynaya N，Schonfeld D.Theoretical foundations of spatially-variant mathematical morphology part II: gray-level images[J].IEEE Trans on Pattern Analysis and Machine Intelligence, 2008, 30(5):837-850.

[13] Bouaynaya N，Schonfeld D. Spatially variant morphological image processing: theory and applications[C]// SPIE.SPIE Visual Communication and Image Processing. San Jose: SPIE, 2006,6077：2-4.