例析数列通项公式的几种特殊求法

广东省广州市从化中学 (510900) 李希胜

求数列的通项公式是高考和竞赛的重要内容，通过这部分内容的教学可训练学生的思维能力.求数列通项公式需要较多的知识和较强的能力，常用方法也很多，其中不动点法、特征根法和构造法是非常有效的几种特殊方法.

1.不动点法求数列通项公式

函数不动点定义：若函数y=f(x)的图像与直线y=x有交点M(m,m)，则称m为函数y=f(x)的不动点，其运算特征是f(m)=m.

数列是特殊的函数，一般是把an看作n的函数，但若数列{an}有递推公式an+1=f(an)，则也可把an看作自变量x,an+1看作因变量y，引入函数y=f(x).若函数y=f(x)有不动点m，则可在数列递推关系an+1=f(an)的两边都减去m，构造出新的数列，而新数列一般是等比数列、等差数列或其它特殊数列，易求出其通项公式，进而可求出原数列{an}的通项公式.

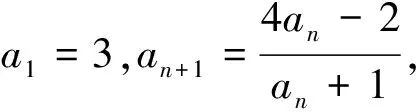
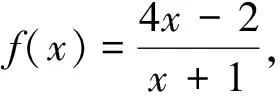
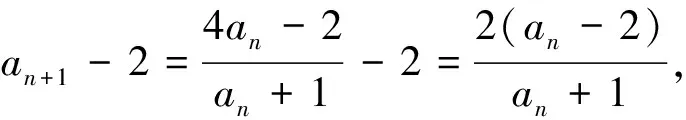
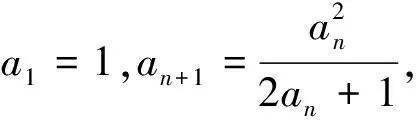
2.特征根法求数列通项公式

在数列{an}中，已知a1，a2,an+2=pan+1+qan(其中p和q为常数),求数列的通项公式.称x2=px+q，即为数列{an}的特征方程.

结论1 对具有递推关系an+2=pan+1+qan的数列，特征方程为x2-px-q=0，当Δ=p2+4q>0时，设两个不等实根为α,β，则数列的通项公式为an=c1αn+c2βn，其中c1,c2为待定系数，可由初始条件确定.

证明：由韦达定理得α+β=p，α·β=-q，将p=α+β和q=-α·β代入递推关系an+2=pan+1+qan得an+2=(α+β)an+1-α·βan,即an+2=αan+1+βan+1-α·βan,从而既有an+2-βan+1=α(an+1-βan)，又有an+2-αan+1=β(an+1-αan).

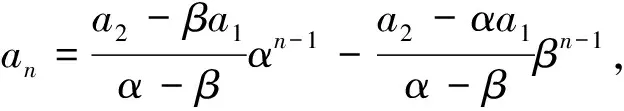
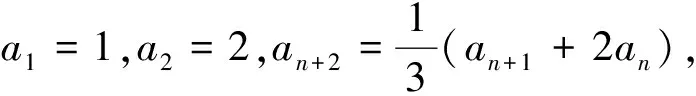
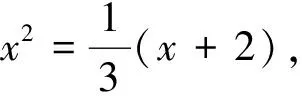
结论2 对具有递推关系an+2=pan+1+qan的数列，特征方程为x2-px-q=0，当Δ=p2+4q=0时，设二重根为α，则数列的通项公式为an=c1αn+c2nαn，其中c1,c2为待定系数，可由初始条件确定.

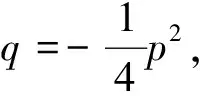
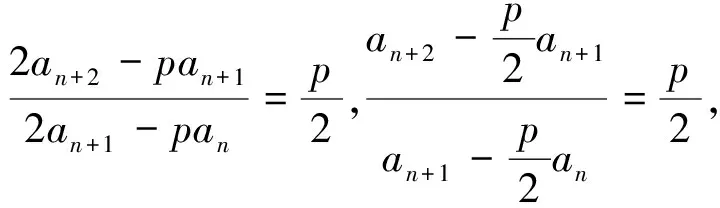
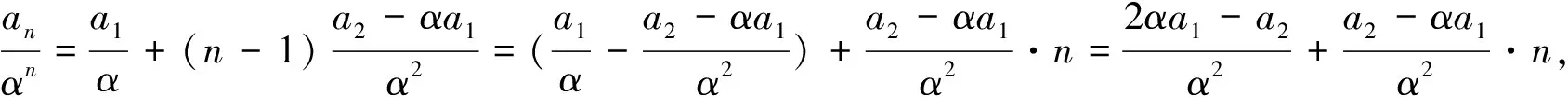
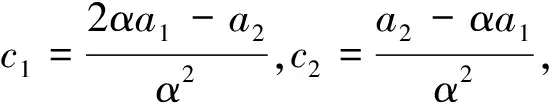
例4 已知数列{an}满足a1=4,a2=12,an+2=4an+1-4an,求数列{an}的通项公式.

解：数列{an}的特征方程为x2-4x+4=0，Δ=0,有二重特征根x=2.

设an=c1·2n+c2·n·2n，分别取n=1,2可得4=c1×21+c2×1×21和12=c1×22+c2×2×22，可解得c1=1，c2=1，故an=2n+n·2n=(n+1)·2n.

结论3 对具有递推关系an+2=pan+1+qan的数列，特征方程为x2-px-q=0，当Δ=p2+4q<0时，无特征根，则数列为周期性的数列.

例5 已知数列{an}满足a1=3,a2=6,an+2=an+1-an,求a2018的值.

解：特征方程为x2=x-1，即x2-x+1=0，Δ=-3<0，数列必有周期性，a1=3,a2=6,a3=3，a4=-3，a5=-6，a6=-3,a7=3,a8=6，周期为6，a2018=a2=6.

3.构造法求数列通项公式

构造法就是以已知条件为原料，以所求结论为方向，构造出一种新的数学形式，使得问题在这种形式下简捷地得到解决.

例6 已知a1=2，an+1=4an-3n+1，求数列{an}的通项公式.

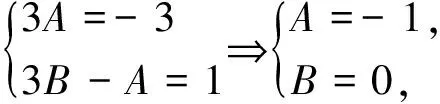
例7 已知a1=0，an+1=3an+2n+4n，求数列{an}的通项公式.

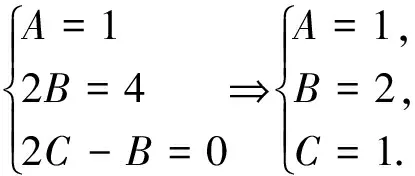
故an+1+2n+1+2(n+1)+1=3(an+2n+2n+1)，数列{an+2n+2n+1}为等比数列，首项为a1+21+2×1+1=5，公比为3，从而an+2n+2n+1=5×3n-1，an=5×3n-1-2n-2n-1.